Спектральное представление случайных процессов
Используется прямое и обратное преобразование Фурье
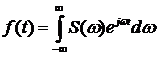
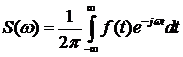
Первый интеграл позволяет представить непериодическую функцию в виде суммы синусоид с непрерывной последовательностью частот.
Функция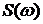 
называется спектральной плотностью и характеризует плотность амплитуд в полосе частот 
.
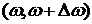Найдем спектральную плотность для функции Дирака, обладающей свойствами
, 
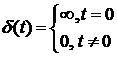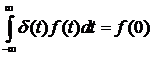
Как следствие, получаем
.
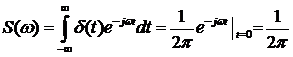Таким образом, спектральная плотность постоянна и равна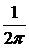 
. Используя эту спектральную плотность можно получить
.
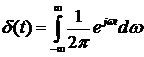Откуда
.
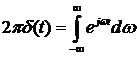В спектральной теории случайных процессов вместо функции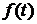 
вводится корреляционная функция 
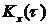. В этом случае
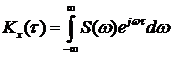
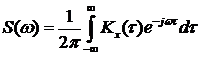
Учитывая, что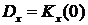 
получим
.
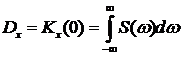Из этого выражения следует, что дисперсия является суммой элементарных слагаемых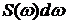 
. Если этот интеграл представить в виде бесконечной суммы, то на 
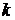-ю гармонику будет приходиться дисперсия
.
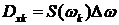Это равенство показывает, что спектральная плотность случайного процесса характеризует плотность распределения дисперсий по частотам непрерывного спектра. Размерность спектральной плотности есть отношение дисперсии случайного процесса к частоте
.
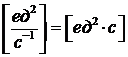Белый шум
Процесс, для которого во всем диапазоне частот спектральная плотность постоянна
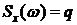
называется белым шумом
. Найдем корреляционную функцию случайного процесса, у которого спектральная плотность постоянна на всех частотах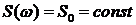 
.
|
|
|
.
Используя полученное ранее соотношение 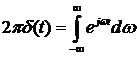имеем , что корреляционная функция белого шума имеет вид
.
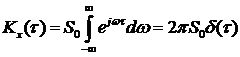Представим это равенство в виде
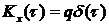
где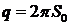 
называется интенсивностью белого шумаи имеет размерность спектральной плотности.
Поскольку белый шум является абстрактным процессом, то разумным является введение белого шума с ограниченным спектром
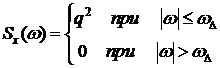
т.е. у которого спектральная плотность постоянна и отлична от нуля в определенной полосе частот (см. рис.)
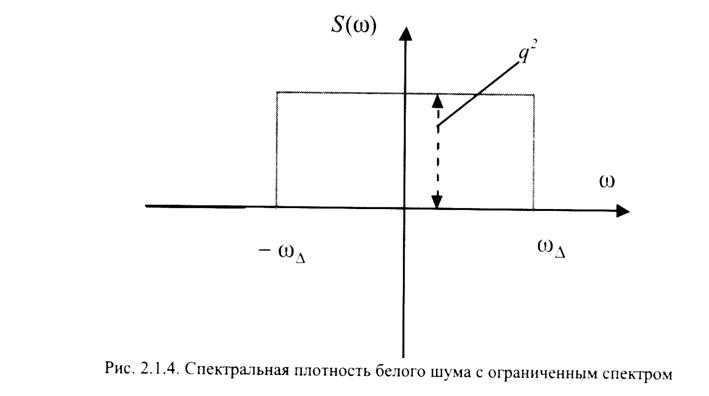
Получим корреляционную функцию такого процесса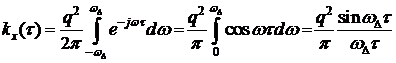 
В частности при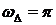 
имеем
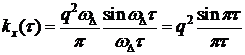
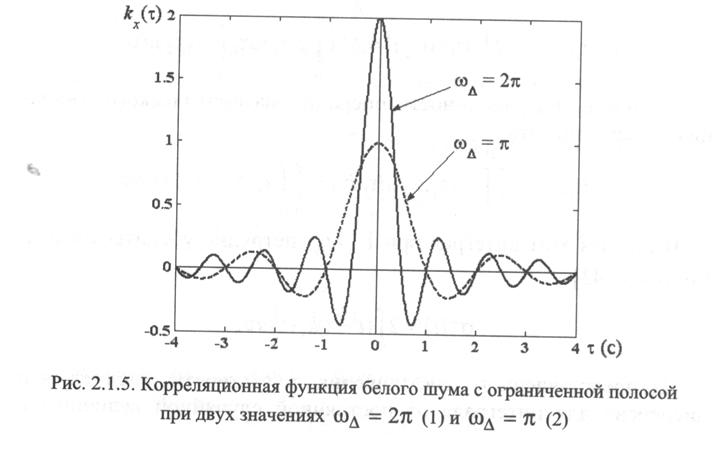
Отметим, что в пределе при увеличении полосы пропускания корреляционная функция стремится к дельта функции.
Экспотенциально-коррелированный случайный процесс
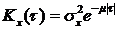
где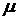 
-коэффициент затухания корреляционной функции.
Пример . Корреляционная функция имеет вид
.
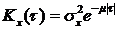Найти спектральную плотность.
Решение.
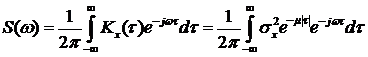
Пользуясь свойством модуля
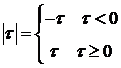
получим
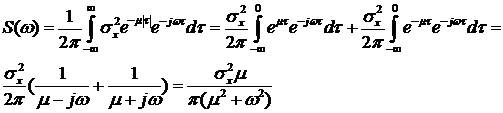
Вид корреляционной функции и спектральной плотности показан на рисунке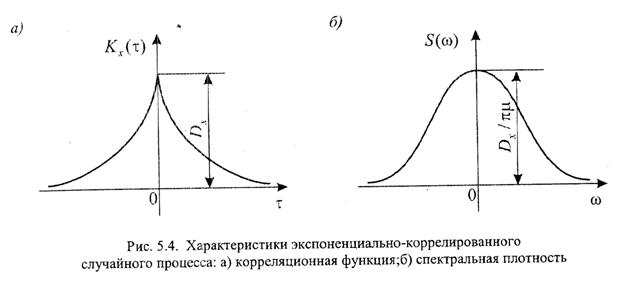 
Прохождение случайного процесса через линейную систему
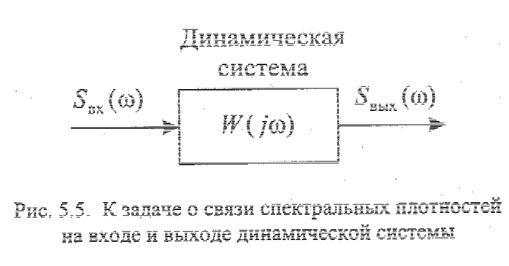
Для решения задачи нужно воспользоваться известным соотношением
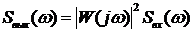
Если поставить задачу минимизации дисперсии можем записать
.
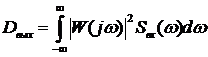Дата добавления: 2018-06-27; просмотров: 860; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!