Ошибки БИНС, вызванные дрейфом гироскопов
Пусть датчик угловой скорости имеет ошибку ,а остальных возмущений нет.
,а остальных возмущений нет.
Найдем ошибку в определении угла тангажа.
Тангаж определяется интегрированием относительной угловой скорости связанного трехгранника

Расчетное значение угла тангажа можно представить в виде

где  - рассчитанная с помощью БИНС проекция угловой скорости географического трехзгранника.
- рассчитанная с помощью БИНС проекция угловой скорости географического трехзгранника.
Запишем выражение для ошибки выработки тангажа

где  -.
-.
Дифференцируя обе части равенства, получим

Связь между истинным и вычисленным значением тангажа в соответствии с рисунком определяется выражением

или
 .
.
Таким образом при однаканальном анализе БИНС ошибка тангажа равняется ошибке построения вертикали взятой с обратным знаком и можно записать следующее дифференциальное уравнение

Так как 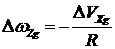 , получим
, получим
 .
.
Учитывая, что

это уравнение примет вид

Найдем решение этого уравнения для постоянной скорости ухода. Дифференцируя , получим

Решая это уравнение будем иметь для 

и по аналогии с рассмотренным материалом будем иметь



Таким образом, вычисленная вертикаль совершает колебания с периодом Шулера относительно истинной вертикали с амплитудой равной  . В ошибке определения скорости имеется постоянная составляющая пропорциональная радиусу Земли. Наличие этой погрешности приводит к накапливающейся погрешности в координате и пройденном расстоянии, что является главным недостатком БИНС. Поведение ошибок иллюстрируется рисунком
. В ошибке определения скорости имеется постоянная составляющая пропорциональная радиусу Земли. Наличие этой погрешности приводит к накапливающейся погрешности в координате и пройденном расстоянии, что является главным недостатком БИНС. Поведение ошибок иллюстрируется рисунком 
Ошибки вертикального канала БИНС
Найдем ошибку вертикального канала БИНС
 ,
,
где 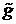 - расчетное ускорение силы тяжести, вводимое для компенсации истинного ускорения.
- расчетное ускорение силы тяжести, вводимое для компенсации истинного ускорения.
Отсюда можно найти
 .
.
где 
При этом ошибка в вычислении высоты будет определяться выражением
 .
.
Полагая  , получим
, получим

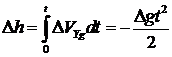
Таким образом ошибки в вертикальной скорости и координате растут неограниченно.
Аналогичные ошибки будут вызваны также смещением нуля вертикального акселерометра.
Структурная схема ошибок северного канала БИНС
Просуммируем полученные результаты
 ,
,
 ,
,
 ,
,
 .
.
Как следствие структурную схему северного канала БИНС можно представить в
виде

Пользуясь правилами преобразования структурных схем фрагмент этой схемы может быть преобразован к виду

Из этого рисунка можно заключить, что вектор ускорения силы тяжести приводит к образованию отрицательной обратной связи. На структурной схеме ошибок БИНС.
Векторная модель ошибок БИНС
Получим векторную модель ошибок БИНС с географическим опорным трехгранником. В основе алгоритма БИНС лежит пересчет данных, измеренных в связанной системе координат в географическую, когда матрица перехода  известна. Эту матрицу можно найти решая уравнение Пуассона
известна. Эту матрицу можно найти решая уравнение Пуассона
 ,
,
где
 ,
, 
При решении задачи определения матрицы  в БИНС используеится информация об абсолютных угловых скоростях
в БИНС используеится информация об абсолютных угловых скоростях  , известных с ошибками.
, известных с ошибками.
Вводя в рассмотрение кососимметрическую матрицу

можем записать
 .
.
Что касается 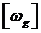 , то вместо нее используется матрица
, то вместо нее используется матрица  , соответствующая скорости географического трехгранника, вычисленного с помощью навигационного алгоритма БИНС.
, соответствующая скорости географического трехгранника, вычисленного с помощью навигационного алгоритма БИНС.
Как следствие , в алгоритме БИНС будет использована матрица  , приводящая к другому вычисленному географическому трехграннику
, приводящая к другому вычисленному географическому трехграннику  . Определим положение этого трехгранника с помощью трех малых углов
. Определим положение этого трехгранника с помощью трех малых углов  поворота. Угол
поворота. Угол  характеризует азимутальную ошибку БИНС , а углы
характеризует азимутальную ошибку БИНС , а углы  ошибку построения вертикали (см. рисунок)
ошибку построения вертикали (см. рисунок)

Результаты поворота приведены в таблице

Полную совокупность преобразований определим как
 .
.
Или в матричной форме

где
 ,
,  ,
,  .
.
Как следствие матрица  представима в виде
представима в виде

Отметим, что матрица  ортогональная.
ортогональная.
Введем матрицу ошибок 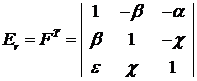
Таким образом , эта матрица характеризует переход от трехгранника  к трехграннику
к трехграннику 
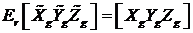 .
.
Эту матрицу можно представить в виде
 .
.
Приступим к выводу уравнений ошибок БИНС.
Учитывая, что
 и
и 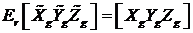 получим
получим
 .
.
Умножая обе части этого равенства на  получим
получим

Откуда

и
 . (*)
. (*)
Это равенство связывает идеальную матрицу преобразования с расчетной матрицей, которая фактически используется в алгоритмах БИНС.
Используя уравнение Пуассона

получим
 .
.
Для матрицы  также можно записать обобщенное уравнение Пуассона
также можно записать обобщенное уравнение Пуассона

Тогда можно получить следующее выражение
 .
.
Учитывая, что
 получим
получим
 .
.
домножая теперь на  , получим следующее выражение
, получим следующее выражение

Из формулы (*)  вытекает, что
вытекает, что  и
и  и это выражение можно записать в виде
и это выражение можно записать в виде

Кососимметрическую матрицу  представим в виде суммы
представим в виде суммы
 ,
,
где  -кососимметрическая матрица ошибок выработки угловых скоростей географического трехгранника
-кососимметрическая матрица ошибок выработки угловых скоростей географического трехгранника
Легко показать, что эта матрица равна

и дифференциальное уравнение для ошибок можно представить в виде

где  -кососиметрическая матрица элементами которой являются дрейфы уходов гароскопов, спроектированных в географическую систему координат
-кососиметрическая матрица элементами которой являются дрейфы уходов гароскопов, спроектированных в географическую систему координат
Пренебрегая в этом уравнении элементами второго порядка малости
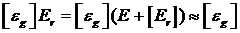 ,
,
 ,
,
и учитывая, что

можем записать
 .
.
Таким образом, это уравнение характеризует азимутальную ошибку и ошибки построения вертикали БИНС в линейном пространстве элементами которого являются кососимметрические матрицы.
Если рассмотреть ошибки ориентации БИНС в векторном пространстве легко показать, что, если ввести вектор конечного поворота
 ,
,
где  -орты осей
-орты осей  ,
,
то поведение этого вектора будет описываться уравнением
 .
.
Таким образом, это уравнение является аналогом описания ошибок ориентации в векторном пространстве.
Найдем погрешности векторного кажущегося ускорения  .
.
Алгоритм идеального режима работы имеет вид
 ,
,
В БИНС фактически реализуется матричное неравенство

Запишем уравнение для ошибок
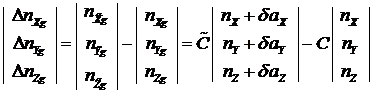 .
.
Учитывая, что  ,
,  получим
получим

Полагая ошибки акселерометров малыми величинами пренебрежем величинами второго порядка малости . Тогда с учетом  Получим
Получим

Вспоминая, что произведение кососимметрической матрицы на столбцевую матрицу эквивалентно векторному произведению можем записать
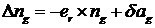 .
.
Представляя вектор  в виде суммы
в виде суммы
 ,
,
где 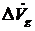 -вектор ошибок выработки линейной скорости,
-вектор ошибок выработки линейной скорости,  -вектор ошибок компенсации вредных ускорений
-вектор ошибок компенсации вредных ускорений
получим выражение для ошибок выработки составляющих скорости
 .
.
Скалярная модель ошибок БИНС
Определим скалярный вид уравнений
 ,
,
 .
.
Найдем компоненты вектора ошибок угловой скорости 
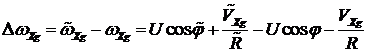

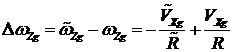 .
.
Представим вычисленные значения в виде суммы
 ,
,  ,
,  ,
, 
 .
.
Пренебрегая величинами второго порядка малости, получим
 ,
,
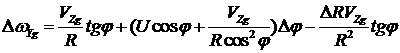 ,
,
 .
.
Учитывая, что  ,
, 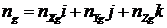 и вычисляя векторные произведения, получим следующую систему ошибок БИНС
и вычисляя векторные произведения, получим следующую систему ошибок БИНС
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Погрешности компенсации вредных ускорений можно найти раскладывая выражения в ряд Тейлора. В линейном приближении они будут иметь вид
 ,
,
 ,
,

Аналогично можно определить погрешности выработки координат
 ,
,


Таким образом , полная система ошибок БИНС в скалярном виде имеет вид



 ,
,
 ,
,
 .
.
 ,
,

 .
.
Дата добавления: 2018-06-27; просмотров: 1491; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
