Уравнения ошибок БИНС в определении параметров ориентации
Представим формулу
 .
.
Тогда

и как следствие,

Найдем ошибки для случая малого тангажа и крена
В этом случае матрица перепроектирования приближенно имеет вид

Представим углы в виде сумм двух составляющих.
Тогда

С другой стороны эта матрица равна

Приравнивая, получаем
 ,
,
 ,
,
 .
.
Пренебрегая в первом уравнении произведением малых величин можем записать


 .
.
Для того чтобы найти ошибки азимутальной ориентации нужно знать ошибки построения вертикали. Ошибка определения рыскания 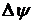 определяется только азимутальной ошибкой
определяется только азимутальной ошибкой  .
.
Полная система уравнений ошибок БИНС



 ,
,
 ,
,
 .
.
 ,
,

 .
.
В этих уравнениях ошибки чувствительных элементов имеют вид




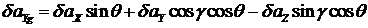 ,
,

Комплексные навигационные системы
Хотя инерциальная навигация обладает неоспоримым преимуществом-автономностью , ей присущ существенный недостаток-накопление ошибок с течением времени.Для устранения этого недостатка используют комплексирование показаний инерциальных систем с показаниями других систем , основанных на других физических принципах( спутниковых навигационных систем, астронавигационных и радионавигационных систем, корреляционно-навигационных систем и т.д.)
Объединение информации различных измерителей осуществляется на основе моделей их погрешностей, являющимися случайными процессами.
В основу теории случайных процессов положено пять основных неслучайных функций, характеризующих процесс:
|
|
|
- математическое ожидание случайного процесса -характеризует поведение процесса в среднем;
-дисперсияслучайного процесса -характеризует рассеивание значений процесса по времени относительно среднего значения;
плотность распределения- дает представление о распределении процесса в фиксированные моменты времени;
-корреляционная функция- характеризует степень зависимости между двумя сечениями случайного процесса;
-спектральная плотность- дает спектральное представление случайного процесса.
Математическое ожидание

представляет собой функцию времени и позволяет ввести понятие центрированного случайного процесса
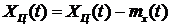 .
.
Дисперсия и среднее квадратическое отклонение


Функция распределения и плотность распределения

Двумерный закон распределения
 .
.
Плотность распределения
 ,
,  .
.
Нормальный (гауссовский) случайный процесс имеет плотность распределения

Для этого процесса вероятность попадания в трубку  составляет 0.997.
составляет 0.997.

Корреляционная функция
 .
.
Свойства корреляционной функции


Векторный случайный процесс
Пусть 
И пусть

Тогда взаимную корреляционную функцию можно представить в виде матрицы
|
|
|
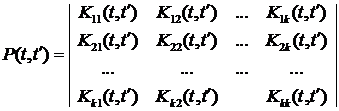
Случайные процессы являются некоррелированными, если  при
при  .
.
Если  ковариационная матрица обозначается как функция одного аргумента и называется корреляционной матрицей случайного векторного процесса
ковариационная матрица обозначается как функция одного аргумента и называется корреляционной матрицей случайного векторного процесса  . В этом случае на главной диагонали стоят дисперсии составляющих вектора.
. В этом случае на главной диагонали стоят дисперсии составляющих вектора.
Для двух случайных векторов  и
и  вводится взаимная матричная корреляционная функция
вводится взаимная матричная корреляционная функция
 .
.
Стационарные случайные процессы
у которых
 ,
, 
Рассмотрим корреляционную функцию
 .
.
Если положить  получим
получим
 .
.
Таким образом, корреляционная функция стационарного случайного процесса является функцией одного аргумента

И как следствие для стационарного процесса имеем
 .
.
В общем случае дисперсия определяется как

и для стационарного процесса имеем
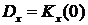 .
.
Дата добавления: 2018-06-27; просмотров: 559; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
