Сформулировать и доказать критерий оптимальности решения задачи линейного программирования при отыскании максимума линейной функции симплексным методом.

 

 

Базисное решение является оптимальным тогда и только тогда, когда в уравнении среди коэффициентов Δ _j при неизвестных нет ни одного отрицательного, т.е оценки Δ _j ≥ 0. Так как двойственные оценки – это взятые с противоположным знаком коэффициенты выражения ц.ф. через свободные неизвестные. Значит, сами эти коэффициенты ≤ 0. Поэтому, как только любая из свободных неизвестных примет положительное значение – целевая функция уменьшается. А это и означает, что она максимальна при нулевых значениях свободных неизвестных, т.е. для данного базисного решения.

 

Допустим необходимо максимизировать целевую функцию L=c₁x₁+c₂x₂+...c_nx_n (1), при условиях:

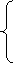x₁  + g_1,m+1x_m+1 + ... + g_1nx_n = h₁,

x₂ + g_2,m+1 x_m+1 + ... + g_2nx_n = h₂, (2)

...     ...               ...  ...

x_m + g_m,m+1 x_m+1 + ... + g_mnx_n = h_m

и x_j≥0, j = 1,2,...n (3).

Для решения такой задачи применяется симплексный метод линейного программирования.

Одним из допустимых решений задачи ЛП будет базисное неотрицательное решение системы (2): x₁=h₁, x₂=h₂,...x_m=h_m, x_m+1=0,...x_n=0 (4), ему соответствует значение целевой ф-ии равное:

L₀=c_1оh₁+c₂h₂+...c_mh_m+c_m+1*0+...+c_n*0 = c_i h_i (5).

Надо исследовать, является ли базисное неотрицательное решение (4) оптимальным,т.е. является ли значение (5) наименьшим из всех возможных значений целевой ф-ии (1), отвечающих различным неотрицательным решениям системы (2).

Учитывая, что система уравнений (2) имеет предпочитаемый вид, находим для нее общее решение: x_i=h_i-g_i,m+1x_m+1-...-g_inx_n, i=1,2,...,m (6). Если свободным неизвестным придавать какие-нибудь неотрицательные значения, то будем получать различные решения системы (2), среди которых нас интересуют только неотрицательные. Подставляя их компоненты в линейную форму (1), можно подсчитать соответствующие значения целевой функции. Очевидно, чтобы легче было следить за поведением целевой функции, целесообразно выразить ее только через свободные неизвестные.

Если переписать выражение (1) в виде:   

- L+c₁x₁+c₂x₂+...c_mx_m+ c_m+1x_m+1+...+c_nx_n=0 (7). Для того чтобы исключить базисные неизвестные из этого уравнения, достаточно умножить первое уравнение системы (2) на c₁, второе на c₂ и т.д., сложить полученные произведения и из результата вычесть уравнение (7). Получим L+∆_m+1x_m+1+...+∆_nx_n=L₀ (8), где ∆_j = c₁g_1j + c₂g_2j + ... + c_mg_mj - c_j , j=1,2,...n (9) или ∆_j = z_j - c_j, z_j= c_ig_ij, j=1,2,...n (9a).

Из выражения следует, что базисное решение x₁=h₁, x₂=h₂,...x_m=h_m, x_m+1=0,...x_n=0 (2) является оптимальным решением задачи ЛП

Базисное решение является оптимальным решением задачи ЛП тогда и только тогда, когда в уравнении среди коэффициентов при неизвестных нет ни одного отрицательного, т. е. условие оптимальности имеет вид ∆j≥0 , j=1,2,…,n.

Если же хотя бы один из коэффициентов при свободных неизвестных равен нулю, то будут и небазисные оптимальные решения. Очевидно, оптимальных решений будет еще больше, если среди коэффициентов при свободных неизвестных в уравнении (8) окажется несколько нулевых.

 

 

---

Дата добавления: 2018-06-01; просмотров: 336; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!