Получить выражение целевой функции z через свободные переменные общего решения системы ограничений

           Х₁                                     1                       S

          Х₂                                                                                 1        

          Х₃                                                                                             1

40=X₁+ 7X₄+2X₁

H=X₁+SX₂→X₁=H-SX₂

Что представляет собой симплексная таблица?

Симплекс-таблица составляется из коэффициентов при x₁, x₂, x₃, x₄ и чисел, стоящих в правых частях уравнений-ограничений задачи: в первой строке записываются элементы уравнения (А), во второй - (В). В последней строке симплекс-таблицы записываются коэффициенты и правая часть целевой функции (С). Таким образом, симплекс-таблица содержит две строки коэффициентов (по числу ограничений задачи) и строку коэффициентов целевой функции. Число столбцов в симплекс-таблице равно числу переменных задачи плюс один столбец правых частей (b).

Правила выбора ключевого столбца и строки при решении задачи ЛП симплексным методом, последствия неправильного выбора

1)Ключевой столбец выбираем по минимальной двойственной оценке

2)Потом считается столбец альфа как отношение свободного члена к коэффициенту ключевого столбца

3)По минимальной альфа выбираем ключевую строку

В качестве разрешающей неизвестной можно принять любую неизвестную, при которой есть хоть один положительный коэффициент, а затем в качества разрешающего уравнения следует взять то уравнение, которое соответствует наименьшему среди отношений свободных членов уравнений к соответствующим положительным коэффициентам при выбранной неизвестной в этих уравнениях. Условимся говорить, что СЛАУ подвергается симплексным преобразованиям, если процесс исключения неизвестных осуществляется в соответствии с указанными правилами выбора разрешающей неизвестной и разрешающего уравнения. Остается заметить, что СЛАУ не будет иметь ни одного неотрицательного решения, если в процессе симплексных преобразований в ней появится уравнение, в котором свободный член строго положителен, а среди коэффициентов при неизвестных нет ни одного положительного.

Введение искусственных переменных в систему ограничений задачи ЛП при решении задачи ЛП методом искусственного базиса: цель и правило введения

Метод искусственного базисаприменяется к решению задач линейного программирования в общем случае, когда система ограничений не имеет предпочитаемого вида.

Пусть требуется минимизировать 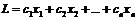 (1) при ограничениях:

          (2)

.                            (3)

К данной задаче ЛП непосредственно нельзя применить симплексный метод, т.к. система (2) не имеет предпочитаемого вида, хотя правые части всех ее уравнений можно считать неотрицательными. Поэтому к левой части каждого уравнения системы (2) добавим по одной искусственной неотрицательной неизвестной и образуем следующую систему m линейных уравнений с n+m неизвестными:

       (4)

где            (5)

Очевидно, в системе (4) неизвестные  образуют базисный набор, который принято называть искусственным. Кроме того, образуем искусственную линейную форму:  (6) и сформулируем следующую вспомогательную задачу линейного программирования: минимизировать линейную форму (6) при линейных ограничениях (4) и (5).

Для решения вспомогательной задачи можно применить симплексный метод, так как система (4) имеет предпочитаемый вид, искусственные неизвестные  являются базисными, а правые части всех уравнений неотрицательны. В процессе решения вспомогательной задачи система уравнений (4) будет подвергаться симплексным преобразованиям, в результате которых искусственные базисные неизвестные будут переходить в число свободных, а в базисный набор будут постепенно включаться исходные неизвестные. На некотором этапе процесса решения вспомогательной задачи система уравнений (4) примет такой предпочитаемый вид, что соответствующее базисное решение будет оптимальным решением этой задачи. При этом минимальное значение целевой функции может быть или положительным, или равным нулю, так как функция представляет сумму неотрицательных переменных.

Если S_min<0, то исходная задача не имеет решения ввиду противоречивости условий (2) и (3). Действительно, если допустить, что система уравнений (2) имеет неотрицательное решение (α₁,α₂,...,α_n), то вспомогательная задача будет иметь решение (α₁,α₂,...,α_n,0,0,…,0) для которого S=0, что противоречит предположению.

Если же S=0, то возможна дальнейшая минимизация

Мы поможем в написании ваших работ!