И это равно математическому ожиданию проигрыша второго игрока.

⇐ Преды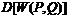дущаяСтр 6 из 22Следующая ⇒

Пусть есть дисперсия этой случайной величины. Естественно назвать среднее квадратическое отклонение с.в. 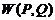, т.е. 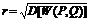риском для первого при игре со стратегиями 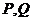. Поскольку выигрыш первого есть проигрыш для второго, то 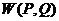есть случайный проигрыш второго и 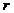вполне естественно можно назвать риском игры с такими стратегиями и для второго.

Предположим сначала, что игроки озабочены только максимизацией среднего дохода за партию игры – обычная цель в таких играх. Тогда игроки будут играть со своими оптимальными стратегиями: 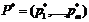– Первый игрок и 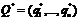– второй, стратегии оптимальны, если М(P,Q*) 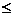М(P*,Q*) 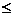М(P*,Q)

Пара (P*,Q*) – решение игры. Математическое ожидание с. в. 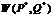называется ценой игры, обозначим ее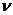

Основные понятия в теории графов: Дуги, вершины в ориентированном и неориентированном графе. Примеры применения теории графов в экономике.

Граф-это совокупность двух множеств: множества Х, элементы которого называют вершинами, и множества У упорядоченных пар вершин, элементы которого называют дугами или ребрами. Если отрезки, соединяющие вершины графа, имеют направления, то граф называется ориентированным, а сами отрезки — дугами. Если же отрезки не имеют направления, то граф называется неориентированным, и в этом случае говорят, что вершины графа соединены ребрами.

Применение в экономике: задача выбора кратчайшего пути от пункта производства до пункта конечного потребления, задача выбора схемы подключения домов к системе кабельного телевидения, при которой общая длина всех участков минимальна, задача определения максимального объема информации, который можно передать от определенного отправителя к конкретному получателю, с учетом пропускных способностей каналов и узлов системы передачи данных.

Сформулировать и доказать критерий оптимальности решения задачи линейного программирования при отыскании минимума линейной функции симплексным методом.

Для того, чтобы базисное решение в задаче лп было оптимальным решением этой задачи необходимо и достаточно, чтобы в оценочном уравнении Z0-Z=Σ∆jxj выполнялось условие ∆j≤0 , j=1,2,…,n

Действительно, если в общем решении мы станем придавать различные неотрицательные значения свободным неизвестным так, чтобы соответствующие базисные неизвестные также принимали неотрицательные значения, то одновременно с частными неотрицательными решениями системы ограничений мы будет получать согласно выражению L=L₀-∆_m+1x_m₊₁-...-∆_nx_n соответствующие им значения целевой функции. В частности, при нулевых значениях свободных неизвестных получится базисное решение x₁=h₁, x₂=h₂,...x_m=h_m, x_m₊₁=0,...x_n=0 и соответствующее ему значение линейной формы L0=Σcihi. Если хотя бы один из коэффициентов при неизвестных в последнем уравнении вспомогательной системы ,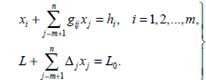

например, Δm+1 положителен, то мы можем соответствующей свободной неизвестной xm+1 дать в общем решении какое-нибудь положительное значение, сохранив 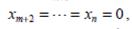, и получить частное неотрицательное решение с меньшим значением линейной формы.

Экономический смысл двойственной задачи к модели оптимального планирования производства. Математическая модель задачи определения расчетных оценок ресурсов

Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание.

В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями данного производственного процесса, характеризуемыми матрицей условий A, со структурой и количеством ресурсов, отпущенных для производственного потребления, описываемых вектором B, а также со структурой внешних цен, на основе которых получается вектор прибылей C. Эти оценки называют расчетными оценками ресурсов. Расчетную оценку единицы ресурса не следует отождествлять с той ценой, по которой предприятию был отпущен этот ресурс. Последняя отражает общественно необходимые затраты на производство единицы ресурса, а расчетная цена показывает только сравнительную ценность этого ресурса на данном предприятии в данных конкретных условиях.

В зависимости от вида исходной задачи линейного программирования различают симметричные и несимметричные пары двойственных задач.

Если система ограничений исходной задачи состоит из неравенств и на все переменные х_j наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач.

Пусть исходная задача имеет вид: найти наибольшее значение функции

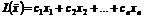
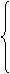
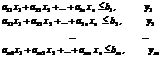
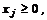
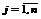
Правило составления двойственных задач

1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y_i, где .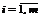

2. Составляется целевая функция 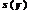, коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:

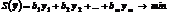(1)

3. Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:

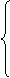
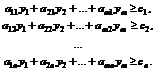(2)

4. Переменные y_i в двойственной задаче также неотрицательны, т.е.

. (3)

Если двойственную задачу принять за исходную и по данному правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным.

В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку.

Дата добавления: 2018-06-01; просмотров: 352; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!