Матричные игры с нулевой суммой, смысл коэффициентов платежной матрицы, примеры матричных игр.

⇐ ПредыдущаяСтр 5 из 22Следующая ⇒

В экономике и управлении часто встречаются ситуации, в которых сталкиваются две или более стороны, преследующие различные цели, причем результат, полученный каждой из сторон при реализации определенной стратегии зависит от действий других сторон. Такие ситуации называются конфликтными. Например: аукцион, спортивные состязания, парламентские выборы (при наличии нескольких кандидатов), карточная игра.

Рассмотрим конфликт двух участников с противоположными интересами. Математической моделью такого конфликта является игра с нулевой суммой. Участники игры называются игроками. Стратегией игрока называется осознанный выбор одного из множества возможных вариантов его действий.

Рассмотрим конечные игры, в которых множества стратегий игроков конечны; стратегии первого игрока пронумеруем от 1 до m, а стратегии второго игрока — от 1 до n.

Если первый игрок выбрал свою i-ю стратегию, а второй игрок — свою j-ю стратегию, то результатом такого совместного выбора будет платеж второго игрока первому. Таким образом, игра с нулевой суммой однозначно определяется матрицей, которая называется платежной. Строки этой матрицы соответствуют стратегиям первого игрока, а столбцы — стратегиям второго игрока.

Игра происходит партиями. Партия игры состоит в том, что игроки одновременно называют свой выбор: первый игрок называет некторый номер строки матрицы, а второй — некоторый номер столбца этой матрицы. После этого происходит «расплата». Пусть, например, первый игрок назвал номер i, а второй — j. Тогда второй игрок платит первому сумму. На этом партия игры заканчивается. Если a_ij>0, то это означает, что при выборе первым игроком i-й стратегии, а вторым — j-й стратегии выигрывает первый игрок.

Цель каждого игрока — выиграть как можно большую сумму в результате большого числа партий. Стратегия называется чистой, если выбор игрока неизменен от партии к партии.

При любой стратегии первого игрока, второй игрок будет выбирать стратегию обеспечивающий ему наибольший выигрыш, поэтому с точки зрения первого игрока надо выбирать такую стратегию, при которой второй игрок, действуя разумно заплатит наибольшую сумму. Такая стратегия первого игрока называется максиминной, а величина =max min a_ij называется нижней ценой игры.

Аналогично (с точки зрения второго игрока) определяется верхняя цена игры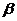 =min max a_ij и соответствующая ей минимаксная стратегия второго игрока. То есть, принимая свою минимаксную стратегию второй игрок проиграет не больше .

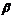В общем случае имеет место неравенство α≤β, если же α=β, то говорят, что игра имеет седловую точку, общее значение и β называется при этом ценой игры.

При этом стратегии игроков, соответствующие седловой точке, называются оптимальными чистыми стратегиями, так как эти стратегии являются наиболее выгодными сразу для обоих игроков.

Смешанной стратегией первого игрока называется вектор , где все , а . При этом — вероятность, с которой первый игрок выбирает свою i-ю стратегию. Аналогично определяются смешанные стратегии второго игрока. Чистая стратегия также подпадает под определение смешанной — если все вероятности равны нулю, кроме одной, равной единице.

Пусть игроки – Первый и Второй, играют в матричную игру с матрицей . Пусть стратегия Первого есть , а Второго – . Тогда выигрыш Первого есть случайная величина (с.в.) с рядом распределения:

W(P,Q):	a₁₁		…		a_ij		…		a_mn
	p₁ q₁		…		p_i q_j		…		p_m q_n

Если игроки применяют свои смешанные стратегииP (p_1,p_2,…p_m )и Q (q₁, q₂,…q_n) соответственно,Выигрыш первого:выигрыш a_ij

Вероятность p_i q_j_.

То есть первый игрок с вероятностьюp_i g_j_.выигрывает a_ij_..Математическое ожидание выигрыша первого игрока равноМ(P,Q)= 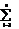p_i q_j a_ij есть средний выигрыш.

Дата добавления: 2018-06-01; просмотров: 571; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!