В каком случае процесс решения задачи ЛП симплекс-методом является конечным?
В любом.
Запишите симметричную пару двойственных задач линейного программирования.
Z=c1x1+c2x2+…+cnxn → max F=b1y1+b2y2+….+bmym→min
A11x1+a12x2+…+a1nxn<=b1 a11y1+a21y2+…+am1ym>=c1
A21x1+…+a2nxn<=b2 ……………………………….
…………………… a1ny1+a2ny2+…+amnym>=cn
Am1x1+…+amnxn<=bm
Yi>=0
Xj>=0
Симметричность заключается в том, что в обеих задачах переменные неотрицательны и система ограничений является неравенствами.
Сформулируйте правила составления задачи, двойственной к данной задаче линейного программирования с ограничениями — неравенствами.
В общем случае принято называть двойственной задачей для произвольной задачи ЛП с ограничениями-неравенствами такую задачу ЛП, которая получается из данной задачи следующим образом: каждому ограничению-неравенству исходной задачи ставится в соответствие переменная двойственной задачи, принимающая неотрицательные значения; матрица коэффициентов при неизвестных транспонируется; правые части ограничений заменяются коэффициентами целевой функции; меняются направления неравенств, коэффициенты целевой функции заменяются правыми частями ограничений; от максимизации (минимизации) функции цели переходят к минимизации (максимизации). Говорят, что задачи ЛП обра-зуют симметричную пару.
|
|
|
Матричная запись пары двойственных задач ЛП (симметричная пара задач с ограничениями-неравенствами и несимметричная пара, где в одной из задач ограничения имеют вид равенств)
Прямая задача: матричная запись:
z = c1x1 + c2x2 + … + cnxn. →max cx→max
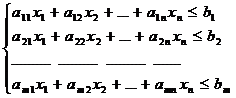Ax≤b
xj≥0 (j=1,n)
(1)
xj ³0, j=1,n
Двойственная задача: (симметричная пара – ограничения явл-ся неравенствами и переменные неотрцательные)
F = b1y1 + b2y2 + … + bmym. →min матричная запись:
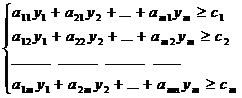yb →min
yA≥c
(1) yi≥0,(i=1,m)
yi ³0, i=1,m
|
|
|
Прямая задача: Матричная запись:
z = c1x1 + c2x2 + … + cnxn. →max cx→max
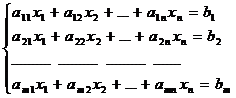Ax=b
xj≥0 (j=1,n)
(1)
xj ³0, j=1,n
Двойственная задача (несимметричная): матричная запись:
F = b1y1 + b2y2 + … + bmym. →min yb →min
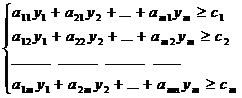yA≥c
yi – любое число (i=1,m)
(1)
Сформулировать и доказать основное неравенство теории двойственности линейного программирования.
Пусть дана пара взаимодвойственных задач, тогда для любых допустимых решений Х=(х1, x2, … xn) исходной задачи и У=(у1, y2,….уm) двойственной задачи справедливо неравенство:
Доказательство:
|
|
|
Основное неравенство теории двойственности ЛП. Малая теорема двойственности и ее экономическое содержание. Теорема о достаточном условии оптимальности решений пары двойственных задач ЛП.
Для любых допустимых решени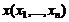й 
и 
прямой и двойственной задач ЛП справедливо неравенство: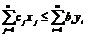 
. Для любого допустимого плана исходной задачи и для любого допустимого в-ра оценок ресурсов 
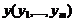общая стоимость всего произведенного продукта не превышает суммарной стоимости ресурсов.
Малая теорема двойственности: Для существования оптимального решения пары двойственных задач необходимо и достаточно существование допустимого решения для каждой из них.
Теорема о достаточном условии оптимальности решений пары двойственных задач: Есл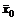и 
и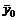 
- допустимые решения пары двойственных задач, для которых выполняется равенство 
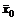, то и 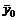- оптимальные решения соответствующих задач.
Согласно этой теореме, план производства продукции и вектор оценок ресурсов является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.
Дата добавления: 2018-06-01; просмотров: 415; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!