Метод параллельных касательных (метод Пауэлла).
Этот метод использует свойство квадратичной функции, заключающееся в том, что любая прямая, которая проходит через точку минимума функции х*,пересекает под равными углами касательные к поверхностям равного уровня функции в точках пересечения (Рис. 2.7).
Этот метод использует свойство квадратичной функции, заключающееся в том, что любая прямая, которая проходит через точку минимума функции х*, пересекает под равными углами касательные к поверхностям равного уровня функции в точках пересечения (Рис. 2.7).
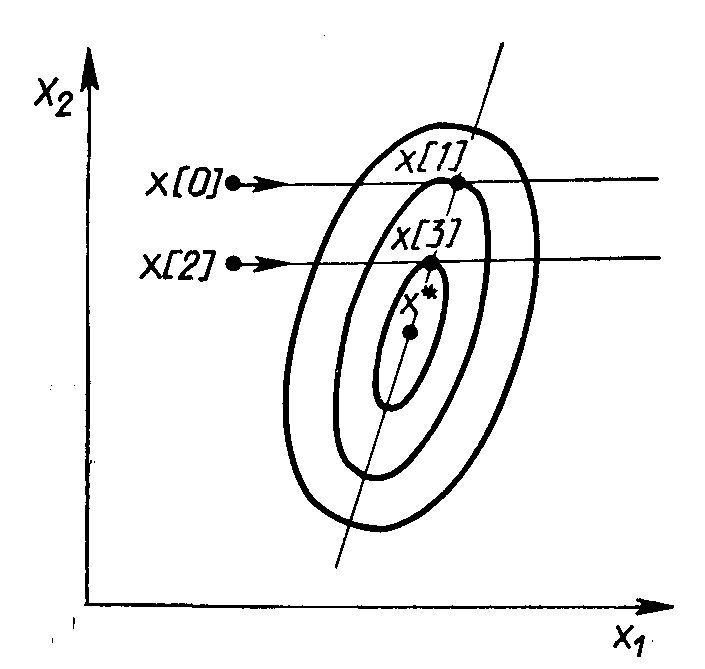
Рис. 2.7. Геометрическая интерпретация метода Пауэлла
Суть метода такова. Выбирается некоторая начальная точка х[0] и выполняется одномерный поиск вдоль произвольного направления, приводящий в точку х[1] . Затем выбирается точка х[2], не лежащая на прямой х[0] - х[1], и осуществляется одномерный поиск вдоль прямой, параллельной х[0] - х[1],. Полученная в результате точка х[3] вместе с точкой х[1] определяет направление x[1] - х[3] одномерного поиска, дающее точку минимума х*. В случае квадратичной функции n переменных оптимальное значение находится за п итераций. Поиск минимума при этом в конечном счете осуществляется во взаимно сопряженных направлениях. В случае неквадратичной целевой функции направления поиска оказываются сопряженными относительно матрицы Гессе. Алгоритм метода параллельных касательных состоит в следующем.
1. Задаются начальной точкой x[0]. За начальные направления поиска р[1], ..., р[0] принимают направления осей координат, т. е р [i] = е[i], i = 1, ..., n (здесь e[i]= (0, ..., 0, 1, 0, … 0)T).
|
|
|
2. Выполняют n одномерных поисков вдоль ортогональных направлений р[i] , i = 1, ..., п. При этом каждый следующий поиск производится из точки минимума, полученной на предыдущем шаге. Величина шага аk находится из условия
f(x[k] + аkр[k]) = 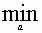 f(x[k] + ар[k]).
f(x[k] + ар[k]).
Полученный шаг определяет точку
х[k+1] = х[k] + аkр[k] .
3. Выбирают новое направление p =-x[n] - х[0] и заменяют направления р[1], ..., р[n] на р[2], ..., р [n], р.Последним присваивают обозначения р[1], ..., р[n]
4. Осуществляют одномерный поиск вдоль направления р = р[n] = х[n] - х[0]. Заменяют х[0] на х[n+1] = х[n] + аnр[п] и принимают эту точку за начальную точку х[0] для следующей итерации. Переходят к п. 1.
Таким образом, в результате выполнения рассмотренной процедуры осуществляется поочередная замена принятых вначале направлений поиска. В итоге после n шагов они окажутся взаимно сопряженными
9 Метод наискорейшего спуска
При использовании метода наискорейшего спуска на каждой итерации величина шага аk выбирается из условия минимума функции f(x) в направлении спуска,т.е. f(x[k]–akf’(x[k]))= 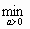 f(x[k]–af'(x[k])).
f(x[k]–af'(x[k])).
Этоусловиеозначает,чтодвижениевдольантиградиентапроисходитдотехпор,показначениефункцииf(x)убывает.Сматематическойточкизрениянакаждойитерациинеобходиморешатьзадачуодномернойминимизациипоафункции
(a)=f(x[k]-af'(x[k])).
|
|
|
Алгоритмметоданаискорейшегоспускасостоитвследующем.
1.Задаютсякоординатыначальнойточких[0].
2.Вточкех[k],k=0,1,2,...вычисляетсязначениеградиентаf’(x[k]).
3.Определяетсявеличинашагаak,путемодномернойминимизациипоафункции(a)=f(x[k]-af'(x[k])).
4.Определяютсякоординатыточких[k+1]:
хi[k+1]=xi[k]–аkf’i(х[k]),i=1,...,п.
5.Проверяютсяусловияостановастерационногопроцесса.Еслионивыполняются,товычисленияпрекращаются.Впротивномслучаеосуществляетсяпереходкп.1.
Врассматриваемомметоденаправлениедвиженияизточких[k]касаетсялинииуровнявточкеx[k+1](Рис.2.9).Траекторияспусказигзагообразная,причемсоседниезвеньязигзагаортогональныдругдругу.Действительно,шагakвыбираетсяпутемминимизациипоафункции?(a)=f(x[k]-af'(x[k])).Необходимоеусловиеминимумафункцииd(a)/da=0.Вычисливпроизводнуюсложнойфункции,получимусловиеортогональностивекторовнаправленийспускавсоседнихточках:
d(a)/da=-f’(x[k+1]f’(x[k])=0.

Рис.2.9.Геометрическаяинтерпретацияметоданаискорейшегоспуска
Градиентныеметодысходятсякминимумусвысокойскоростью(соскоростьюгеометрическойпрогрессии)длягладкихвыпуклыхфункций.УтакихфункцийнаибольшееМинаименьшееmсобственныезначенияматрицывторыхпроизводных(матрицыГессе)
|
|
|

малоотличаютсядруготдруга,т.е.матрицаН(х)хорошообусловлена.Напомним,чтособственнымизначениямиi,i=1,…,n,матрицыявляютсякорнихарактеристическогоуравнения
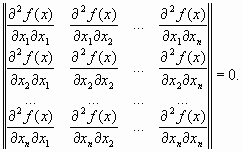
Однаконапрактике,какправило,минимизируемыефункцииимеютплохообусловленныематрицывторыхпроизводных(т/М<<1).Значениятакихфункцийвдольнекоторыхнаправленийизменяютсягораздобыстрее(иногдананесколькопорядков),чемвдругихнаправлениях.Ихповерхностиуровнявпростейшемслучаесильновытягиваются(Рис.2.10),авболеесложныхслучаяхизгибаютсяипредставляютсобойовраги.Функции,обладающиетакимисвойствами,называютовражными.Направлениеантиградиентаэтихфункций(см.Рис.2.10)существенноотклоняетсяотнаправлениявточкуминимума,чтоприводиткзамедлениюскоростисходимости.

Рис.2.10.Овражнаяфункция
Скоростьсходимостиградиентныхметодовсущественнозависиттакжеотточностивычисленийградиента.Потеряточности,аэтообычнопроисходитвокрестноститочекминимумаиливовражнойситуации,можетвообщенарушитьсходимостьпроцессаградиентногоспуска.Вследствиеперечисленныхпричинградиентныеметодызачастуюиспользуютсявкомбинациисдругими,болееэффективнымиметодаминаначальнойстадиирешениязадачи.Вэтомслучаеточках[0]находитсядалекоотточкиминимума,ишагивнаправленииантиградиентапозволяютдостичьсущественногоубыванияфункции.
|
|
|
10 Численные методы безусловной оптимизации второго порядка
Особенности методов второго порядка
Методы безусловной оптимизации второго порядка используют вторые частные производные минимизируемой функции f(х). Суть этих методов состоит в следующем.
Необходимым условием экстремума функции многих переменных f(x) в точке х* является равенство нулю ее градиента в этой точке:
f’(х*) 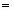 0.
0.
Разложение f’(х) в окрестности точки х[k] в ряд Тейлора с точностью до членов первого порядка позволяет переписать предыдущее уравнение в виде
f'(x) 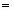 f’(x[k]) + f"(x[k]) (х - х[k])
f’(x[k]) + f"(x[k]) (х - х[k]) 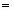 0.
0.
Здесь f"(x[k]) 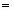 Н(х[k]) - матрица вторых производных (матрица Гессе) минимизируемой функции. Следовательно, итерационный процесс для построения последовательных приближений к решению задачи минимизации функции f(x) описывается выражением
Н(х[k]) - матрица вторых производных (матрица Гессе) минимизируемой функции. Следовательно, итерационный процесс для построения последовательных приближений к решению задачи минимизации функции f(x) описывается выражением
x[k+l] 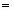 x[k] - H-1(x[k]) f’(x[k]) ,
x[k] - H-1(x[k]) f’(x[k]) ,
где H-1(x[k]) - обратная матрица для матрицы Гессе, а H-1(x[k])f’(x[k]) 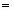 р[k] - направление спуска.
р[k] - направление спуска.
Полученный метод минимизации называют методом Ньютона. Очевидно, что в данном методе величина шага вдоль направления р[k] полагается равной единице. Последовательность точек {х[k]}, получаемая в результате применения итерационного процесса, при определенных предположениях сходится к некоторой стационарной точке х* функции f(x). Если матрица Гессе Н(х*) положительно определена, точка х* будет точкой строгого локального минимума функции f(x). Последовательность x[k] сходится к точке х* только в том случае, когда матрица Гессе целевой функции положительно определена на каждой итерации.
Если функция f(x) является квадратичной, то, независимо от начального приближения х[0] и степени овражности, с помощью метода Ньютона ее минимум находится за один шаг. Это объясняется тем, что направление спуска р[k] 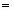 H-1(x[k])f’(x[k]) в любых точках х[0] всегда совпадает с направлением в точку минимума х*. Если же функция f(x) не квадратичная, но выпуклая, метод Ньютона гарантирует ее монотонное убывание от итерации к итерации. При минимизации овражных функций скорость сходимости метода Ньютона более высока по сравнению с градиентными методами. В таком случае вектор р[k] не указывает направление в точку минимума функции f(x), однако имеет большую составляющую вдоль оси оврага и значительно ближе к направлению на минимум, чем антиградиент.
H-1(x[k])f’(x[k]) в любых точках х[0] всегда совпадает с направлением в точку минимума х*. Если же функция f(x) не квадратичная, но выпуклая, метод Ньютона гарантирует ее монотонное убывание от итерации к итерации. При минимизации овражных функций скорость сходимости метода Ньютона более высока по сравнению с градиентными методами. В таком случае вектор р[k] не указывает направление в точку минимума функции f(x), однако имеет большую составляющую вдоль оси оврага и значительно ближе к направлению на минимум, чем антиградиент.
Существенным недостатком метода Ньютона является зависимость сходимости для невыпуклых функций от начального приближения х[0]. Если х[0] находится достаточно далеко от точки минимума, то метод может расходиться, т. е. при проведении итерации каждая следующая точка будет более удаленной от точки минимума, чем предыдущая. Сходимость метода, независимо от начального приближения, обеспечивается выбором не только направления спуска р[k] 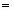 H-1(x[k])f’(x[k]), но и величины шага а вдоль этого направления. Соответствующий алгоритм называют методом Ньютона с регулировкой шага. Итерационный процесс в таком случае определяется выражением
H-1(x[k])f’(x[k]), но и величины шага а вдоль этого направления. Соответствующий алгоритм называют методом Ньютона с регулировкой шага. Итерационный процесс в таком случае определяется выражением
x[k+l] 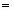 x[k] - akH-1(x[k])f’(x[k]).
x[k] - akH-1(x[k])f’(x[k]).
Величина шага аk выбирается из условия минимума функции f(х) по а в направлении движения, т. е. в результате решения задачи одномерной минимизации:
f(x[k] – ak H-1(x[k])f’(x[k]) 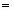
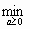 (f(x[k] - aH-1(x[k])f’(x[k])).
(f(x[k] - aH-1(x[k])f’(x[k])).
Вследствие накопления ошибок в процессе счета матрица Гессе на некоторой итерации может оказаться отрицательно определенной или ее нельзя будет обратить. В таких случаях в подпрограммах оптимизации полагается H-1(x[k]) 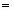 Е , где Е — единичная матрица. Очевидно, что итерация при этом осуществляется по методу наискорейшего спуска.
Е , где Е — единичная матрица. Очевидно, что итерация при этом осуществляется по методу наискорейшего спуска.
Метод Ньютона
Алгоритм метода Ньютона состоит в следующем.
1. В начальной точке х [0] вычисляется вектор
p[0] 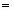 - H-1(x[0])f’([0]).
- H-1(x[0])f’([0]).
2. На k-й итерации определяются шаг аk и точка х[k+1].
3. Вычисляется величина f(х[k+1]).
4. Проверяются условия выхода из подпрограммы, реализующей данный алгоритм. Эти условия аналогичны условиям выхода из подпрограммы при методе наискорейшего спуска. Если эти условия выполняются, осуществляется прекращение вычислений. В противном случае вычисляется новое направление
р[k+1] 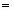 –H-1(x[k])f’([k])
–H-1(x[k])f’([k])
и осуществляется переход к следующей итерации.
Количество вычислений на итерации методом Ньютона, как правило, значительно больше, чем в градиентных методах. Это объясняется необходимостью вычисления и обращения матрицы вторых производных целевой функции. Однако на получение решения с достаточно высокой степенью точности с помощью метода Ньютона обычно требуется намного меньше итераций, чем при использовании градиентных методов. В силу этого метод Ньютона существенно более эффективен. Он обладает сверхлинейной или квадратичной скоростью сходимости в зависимости от требований, которым удовлетворяет минимизируемая функция f(x). Тем не менее в некоторых задачах трудоемкость итерации методом Ньютона может оказаться очень большой за счет необходимости вычисления матрицы вторых производных минимизируемой функции, что потребует затрат значительного количества машинного времени.
В ряде случаев целесообразно комбинированное использование градиентных методов и метода Ньютона. В начале процесса минимизации, когда точка х[0] находится далеко от точки экстремума х*, можно применять какой-либо вариант градиентных методов. Далее, при уменьшении скорости сходимости градиентного метода можно перейти к методу Ньютона.
11.Методы оптимизации. Динамическое программирование.
Основные определения
Задача условной оптимизации заключается в поиске минимального или максимального значения скалярной функции f(x) n-мерного векторного аргументах (в дальнейшем без ограничения общности будут рассматриваться задачи поиска минимального значения функции):
f(x) -> min
при ограничениях:
gi(x) 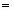 0, i
0, i 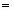 1, ..., k;
1, ..., k;
hj(x) 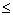 0, j
0, j 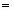 1, .., m;
1, .., m;
a 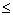 x
x 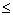 b.
b.
Здесь x, a, b — векторы-столбцы:
 ,
, 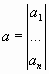 ,
, 
Оптимизируемую функцию f(x) называют целевой функцией. Каждая точка x в n-мерном пространстве переменных x1, ..., х, в которой выполняются ограничения задачи, называется допустимой точкой задачи. Множество всех допустимых точек называется допустимой областью G . Будем считать, что это множество не пусто. Решением задачи считается допустимая точка х*, в которой целевая функция f(х) достигает своего минимального значения. Вектор х* называют оптимальным. Если целевая функция f(x) и ограничения задачи представляют собой линейные функции независимых переменных х1, ..., хn, то соответствующая задача является задачей линейного программировании, в противном случае - задачей нелинейного программирования. В дальнейшем будем полагать, что функции f(x), g(x), i 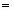 1, ..., k , hj(x), j
1, ..., k , hj(x), j 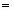 1, …, m, - непрерывные и дифференцируемые.
1, …, m, - непрерывные и дифференцируемые.
Для решения задач оптимизации многостадийных процессов, а также для
процессов, которые могут быть математически описаны как многостадийные
(Рис.4.1), применяется метод динамического программирования.

Рис. 4.1. Многостадийный процесс
Динамическое программирование применяется для оптимизации математически описанных процессов.
Динамическое программирование — это вычислительный метод для решения задач определенной структуры. Метод динамического программирования представляет собой алгоритм определения оптимальной стратегии управления на всех стадиях процесса. При этом закон управления на каждой стадии находят путем решения частных задач оптимизации последовательно для всех стадий процесса. Ограничения на переменные задачи не оказывают влияния на общий алгоритм решения, а учитываются при решении частных задач оптимизации на каждой стадии процесса.
Основные необходимые свойства задач, к которым возможно применить этот принцип:
Задача должна допускать интерпретацию как n-шаговый процесс принятия решений.
Задача должна быть определена для любого числа шагов и иметь структуру, не зависящую от их числа.
При рассмотрении k-шаговой задачи должно быть задано некоторое множество параметров, описывающих состояние системы, от которых зависят оптимальные значения переменных. Причем это множество не должно изменяться при увеличении числа шагов.
Выбор решения (управления) на k-м шаге не должен оказывать влияния на предыдущие решения, кроме необходимого пересчета переменных.
Задача о выборе траектории, задача последовательного принятия решения, задача об использовании рабочей силы, задача управления запасами — классические задачи динамического программирования.
В основе метода динамического программирования лежит принцип оптимальности, сформулированный американским математиком Ричардом Беллманом следующим образом: "Оптимальное поведение обладает тем свойством, что каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, являющегося результатом первого решения"
Щенятский
Дата добавления: 2018-06-01; просмотров: 1074; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
