Конструирование мехатронных устройств и модулей

1.Техническое задание и его основные части

Техническое задание является исходным материалом для создания информационной системы или другого продукта. Поэтому техническое задание (сокращенно ТЗ) в первую очередь должно содержать основные технические требования к продукту и отвечать на вопрос, что данная система должна делать, как работать и при каких условиях. Таким образом, техническое задание является документом, который позволяет как разработчику, так и заказчику представить конечный продукт и впоследствии выполнить проверку на соответствие предъявленным требованиям.

Руководствующими стандартами при написании технического задания являются ГОСТ 34.602.89 «Техническое задание на создание автоматизированной системы» и ГОСТ 19.201-78 «Техническое задание. Требования к содержанию и оформлению». Первый стандарт предназначен для разработчиков автоматизированных систем, второй для программных средств (разницу между данными сериями мы обсуждали в статье «Что такое ГОСТ»).

Опираясь на таблицу из ГОСТов, мы можем выделить основные разделы технического задания:

• Общие сведения о системе (программе);

• Назначение, цели и задачи системы (программы);

• Требования к системе (функциональные требования, пользовательские требования, требования к системе в целом и тд);

• Требования к видам обеспечения;

• Требования к документированию;

• Стадии и этапы разработки;

• Порядок контроля и приемки системы (программы).

Общие сведения

Данный раздел документа Техническое задание должен содержать полное наименование системы и все варианты сокращений, которые будут использованы при разработке документации.

Пример:

«В данном документе создаваемая информационная система называется «Единое окно доступа к образовательным ресурсам», сокращенно ЕО.

Систему Единое окно доступа к образовательным ресурсам далее в настоящем документе допускается именовать Единое окно или Система.»

Также сюда следует включить подразделы сообщающие реквизиты организаций участвующих в разработке (Заказчика и Исполнителя).

В подразделе «Основания для разработки» документа Техническое задание перечисляются основные документы, на основании которых выполняются данные работы. Например, для системы, выполняемой по заказу Правительства страны или другого Государственного органа, должны быть указаны законы, указы и постановления Правительства.

Далее следует указать сроки начала и окончания работ и сведения об источнике финансирования. Данная информация может быть указана и в конце технического задания в разделе с указанием стадий и этапов работ.

Неотъемлемой частью документа Техническое задание также должен быть список терминов и сокращений. Термины и сокращения лучше представить в виде таблицы с двумя столбцами «Термин» и «Полная форма».

Термины и сокращения располагаются в алфавитном порядке. В первую очередь принято давать расшифровку русскоязычным терминам и сокращениям, потом англоязычным.

Назначение и цели создания системы

Данный раздел документа Техническое задание должен содержать назначение и цели создания системы.

Пример:

«Информационная система «Единое окно доступа к образовательным ресурсам» предназначена для обеспечения пользователей полной, оперативной и удобной информацией, касающейся системы образования Российской федерации, организаций выполняющих функцию образовательных учреждений.

Основной целью Системы является формирование единой информационной среды и автоматизации бизнес-процессов Образовательных учреждений Российской Федерации.

Создание информационной системы «Единое окно» должно обеспечить:

• предоставление пользователям широкого спектра информационных ресурсов;

• повышение уровня информационной безопасности;

• повышение эффективности работы образовательных учреждений и ведомств за счет оптимизации ряда бизнес-процессов;

• повышение эффективности процесса взаимодействия информационных систем и сервисов внутри ведомства.

Создание Системы позволит сократить эксплуатационные затраты в результате повышения эффективности работы ведомства.»

Требования к системе

Данный раздел документа Техническое задание предназначен для описания основных функциональных требований системы. Это самая важная часть технического задания, так как именно она станет основным вашим аргументом при спорах с Заказчиком в процессе сдачи системы в эксплуатацию. Поэтому к его написанию необходимо подойти наиболее тщательно.

В документе Техническое задание должны быть представлены все требования, выявленные на этапе проведения анализа объекта автоматизации. Лучше всего выделить основные бизнес-процессы, которые и должны быть раскрыты посредством описания функциональных требований.

Требованиям к видам обеспечения

В данном разделе документа Техническое задание должны быть представлены требования к математическому, информационному, лингвистическому, программному, техническому и др. видам обеспечения (если таковые имеются).

Требования к документированию

Раздел «Требования к документированию» технического задания включает перечень проектных и эксплуатационных документов, которые должны быть предоставлены заказчику.

Данный раздел технического задания также важен, как и описание функциональных требований, поэтому не следует ограничиваться фразой «Заказчику должна быть предоставлена вся документация согласно ГОСТ 34». Это означает, что вы должны предоставить весь пакет документов включая «Формуляр», «Паспорт» и т.п. Большинство документов из списка, указанного в ГОСТ 34.201-89 не нужны ни вам, ни заказчику, поэтому лучше сразу согласовать список на этапе разработки документа Техническое задание.

Минимальный пакет документов обычно включает:

• Техническое задание;

• Ведомость эскизного (технического) проекта;

• Пояснительная записка к Техническому проекту;

• Описание организации информационной базы;

• Руководство пользователя;

• Руководство администратора;

• Программа и методика испытаний;

• Протокол приемочных испытаний;

• Акт выполненных работ

Перечень документов в техническом задании лучше представить в виде таблицы, где указывается наименование документа и стандарт на основании, которого он должен быть разработан.

Стадии и этапы разработки

В данном разделе документа Техническое задание следует представить информацию обо всех этапах работ, которые должны быть проведены.

Описание этапа должно включать наименование, сроки, описание работ и конечный результат.

Порядок контроля и приемки системы

В данном разделе документа Техническое задание необходимо указать документ, на основании которого должны быть проведены приемо-сдаточные испытания.

При необходимости техническое задание может быть дополнено другими разделами, или сокращено путем удаления нецелесообразных пунктов.

При изменении структуры технического задания, во избежание конфликтных ситуаций, ее необходимо согласовать с заказчиком до разработки документа.

2.Структурная схема современных мехатронных модулей.

В состав обобщенной мехатронной системы входят следующие основные компоненты:

механическое устройство, конечным звеном которого является рабочий орган;

блок приводов, включающий силовые преобразователи и исполнитель-ные двигатели;

устройство компьютерного управления, верхним уровнем для которого является человек-оператор, либо другая ЭВМ, входящая в компьютер-ную сеть;

сенсоры, предназначенные для передачи в устройство управления ин-формации о фактическом состоянии блоков машины и движении МС.

Таким образом, наличие трех обязательных частей – механической (точнее электромеханической), электронной и компьютерной, связанных энергетическими и информационными потоками, является первичным признаком, отличающим мехатронные системы.

Электромеханическая часть включает механические звенья и передачи, рабочий орган, электродвигатели, сенсоры и дополнительные электротехнические элементы (тормоза, муфты).

Механическое устройство предназначено для преобразования движений звеньев в требуемое движение рабочего органа.

Электронная часть состоит из микроэлектронных устройств, силовых преобразователей и электроники измерительных цепей.

Сенсоры предназначены для сбора данных о фактическом состоянии внешней среды и объектов работ, механического устройства и блока приводов с последующей первичной обработкой и передачей этой информации в устройство компьютерного управления (УКУ).

В состав УКУ мехатронной системы обычно входят компьютер верхнего уровня и контроллеры управления движением.

Устройство компьютерного управления выполняет следующие основные функции:

Управление процессом механического движения мехатронного модуля или многомерной системы в реальном времени с обработкой сенсорной информации.

Организация управления функциональными движениями мехатронной системы, которая предполагает координацию управления механиче ским движением мехатронной системы и сопутствующими внешними процессами. Как правило, для реализации функции управления внеш-

ними процессами используются дискретные входы/выходы устройства(работающие по принципу «включено-выключено», без «тонкого» регулирования). Математические основы двоичных систем рассматриваются в теме 4 данной учебной дисциплины.

Взаимодействие с человеком-оператором через человеко-машинный интерфейс в режимах автономного программирования (off-line) и непо-средственно в процессе движения мехатронной системы (режим on-line).

Организация обмена данными с периферийными устройствами, сенсо-рами и другими устройствами системы.

Задачей мехатронной системы является преобразование входной информации, поступающей с верхнего уровня управления, в целенаправленное механическое движение с управлением на основе принципа обратной связи.

Мехатронная система не является просто соединением отдельно взятых и физически реализованных компонентов. Их объединение осуществляется на стадии проектирования – это так называемый мехатронный подход к проектированию.

Суть мехатронного подхода к проектированию состоит в интеграции в единый функциональный модуль двух или более элементов возможно даже различной физической природы.

В идеальном для пользователя варианте мехатронный модуль, получив на вход информацию о цели управления, будет выполнять с желаемыми показателями качества заданное функциональное движение. Аппаратное объединение элементов в единые конструктивные модули должно обязательно сопровождаться разработкой интегрированного программного обеспечения.

Программные средства МС должны обеспечивать непосредственный переход от замысла системы через ее математическое моделирование к управлению функциональным движением в реальном времени.

3.Энергетический расчет механической части устройства.

Энергетический расчет привода заключается в расчете основных параметров для выбора двигателя.

В зависимости от задачи, определяются статические моменты, например такие как статический момент при холостом ходе , статический момент при транспортировке груза, инерционные моменты.

Исходя из данныхпараметров ( например Vmax) рассчитывается требуемая скорость вала двигателя:

, .

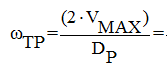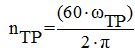Где Vmax - максимальная скорость транспортировки.

Требуемый статический момент двигателя (предварительно) определяется моментом транспортировки металла:

МТР = КЗАП ∙ МТР1, где КЗАП – коэффициент запаса.

Расчет мощности привода

. Согласно исходным данным на проектирование, требуемую мощность привода для выполнения технологического процесса можно найти из формулы:

Р_вых= F_t∙V, (1.1)

где Р_вых – мощность на выходном валу привода, Вт;

F_t – тяговое усилие, Н;

V – скорость движения рабочего органа, м/с;

Или по формуле:

Р_вых= Т_вых∙ω_вых (1.2)

где Р_вых–мощность на выходе, Вт ;

Т_вых – момент на выходном валу, Н∙м;

ω_вых – угловая скорость выходного вала,с-1.

Р_вых= Т_вых∙ω_вых = Твых∙2πn

где n- частота вращения, об/мин.

На основе параметрических расчетов ,можно выбрать нужный двигатель( привод) для разрабатываемого устройства.

4.Конструирование мехатрнных модулей поступательного движения.

Мехатронный модуль движения (ММД) представляет самостоятельное изделие, состоящее из механической, электрической (электротехнической) и информационной частей. Используются индивидуально и в различных комбинациях с другими модулями.

Цель проектирования ММД – преобразование исходных данных в конструкторскую реализацию и соответствующую документацию, по которой может быть изготовлена система, удовлетворяющая сформулированным требованиям.

Задача проектирования ММД – разработать мехатронный модуль поступательного движения на базе двигателя постоянного тока с определенными заданными характеристиками. Требовалось переместить груз массой 20 кг на расстояние 1 300 мм, со скоростью 40 мм/с. Приложенная внешняя нагрузка составила 1 500 H.

Под методикой конструирования будем понимать последовательность, взаимосвязь и взаимо- обусловленность этапов процесса конструирования мехатронного модуля. Разработанный мехатронный модуль, рассматривался как часть некоторой мехатронной подсистемы, которая в свою очередь являлась частью более крупной мехатронной системы. Такое деление может считаться достаточно типичным, так как уровень сложности современных мехатрон- ных систем заставляет уже при проектировании разбивать их на более мелкие подсистемы [2].

Для достижения поставленной цели, проектирование выполняли в две этапа. На первом этапе проектирования была сформулирована задача (определены «входы» и «выходы», а также выявлены существенные связи данного мехатронного модуля с другими частями мехатронной системы и с внешним окружением). На втором этапе была разработана принципиальная схема, выявлены наи- более важные технические характеристики модуля, вытекающие из его схемы и назначения, и затем подробно прорабатывалась конструкция. Разрабатываемый ММД должен быть достаточно рациональным. Критериями рациональности конструкции будем называть те признаки (оценки), по которым можно судить о рациональности соз- даваемого ММД в ходе конструирования. К таким критериям можно отнести технологичность конст- рукции, минимизацию массы, минимизацию габаритов (объема), надежность, экономичность и т. д. Выбор критериев рациональности конструкции зависит от множества взаимосвязанных пере- менных и прежде всего от данных технического задания. Одна из важных частей разработки мехатронного модуля – это анализ последних достижений науки и техники в области мехатроники. Мехатроника как наука не стоит на месте и с каждым днём становится всё более востребованной в таких сферах как армия, безопасность, а также в лабораториях и в быту. Анализ поставленной задачи и возможное направление ее решения, с учетом проведенного патентно-информационного поиска, состоял в поиске уже запатентованных решений поставленной задачи, выбор более оптимального решения и его усовершенствование. Очень важно понимать прин- цип работы будущего ММД, для этого нужно знать, что входит в его состав. Основные его части: ме- ханическое устройство, исполнительные двигатели, силовые преобразователи, устройство компью- терного управления и информационное устройство [3].

Предварительно была разработана схема ММД, которая в дальнейшем при проведении расче- тов уточнялась и корректировалась. Принцип работы ММД состоит в том, что вращение от двигателя передается на цилиндрическую прямозубую передачу. Выходной вал передачи соединен с преобразо- вателем винт-гайка качения и преобразует вращательное движение в поступательное. Далее требова- лось провести расчёт и проверить требуемые передачи на совместимость. Прежде чем приступить к расчёту цилиндрической передачи, необходимо было рассчитать и подобрать двигатели. В резуль- тате расчетов, был выбран наиболее подходящий, удовлетворяющим условиям работы двигатель. При разработке мехатронного модуля поступательного движения на базе двигателя постоянно- го тока необходимо учитывать несколько факторов: – температура среды работы; – условия работы ММД; – конструктивные особенности; – податливость ММД; – последние достижения науки. Каждая из проектируемых частей выполняет в мехатронном модуле свою функцию. Задача вы- полняемого проекта – не просто связать отдельные части в систему с помощью типовых соединений и преобразователей, а сделать конструктивные связи в мехатронном модуле взаимопроникающими и неразрывными. После выбора двигателя рассчитали передачу винт-гайки качения. В данном расчёте рассмот- рели угловые скорости, геометрические параметры, силы и нагрузки, действующие на передачу. В зубчатой цилиндрической передаче определили число ступеней, подобрали материал и рассчитали контактные напряжения. Для каждого из валов были проведены расчёты крутящих моментов, изги- бающих моментов, а также геометрические характеристики валов. Самое важное в расчёте валов – это рассчитать запасы прочности. Особое внимание в расчетах было уделено податливости элемен- тов, входящих в состав ММД, так как передача движения от двигателя к выходному звену мехатрон- ного модуля осуществляется посредством преобразователей движения. Так как данный мехатронный модуль имеет передачу винт-гайка качения, нам потребовалось подобрать направляющую. Выбрали направляющую с трением качения, так как направляющие с тре- ние качения применяют в тех случаях, когда требуется обеспечить легкость и плавность движения. По сравнению с направляющими трения скольжения эти направляющие имеют меньшие потери на трение, долговечны, малочувствительны к перепадам температуры. Выбирая датчик, прежде всего, необходимо было правильно определить приоритеты по следующим критериям: чувствительность, разрешающая способность и точность, линейность, скорость измеряемого процесса, условия применения и класс защиты, надежность, габаритные размеры, стоимость.

5.Конструирование мехатронных модулей вращательного движения.

6.Передачи гибкой связью в мехатронных модулях и принципы их проектирования.

Передачи гибкой связью состоят из ведущего и ведомого шкивов и гибкой связи. По характеру сцепления гибкой связи со шкивами их подразделяют на передачи трением (ременные передачи), передачи с креплением концов гибкой связи к шкивам (ленточные передачи) и передачи зубчатым ремнем.

Работа ременной передачи при использовании сил трения (рисунок 2) связана с упругим скольжением ремня по шкивам, причиной которого является изменение усилия по дуге обхвата от значения F₁ до F₂ на ведущем и от F₂ до F₁ на ведомом шкивах.

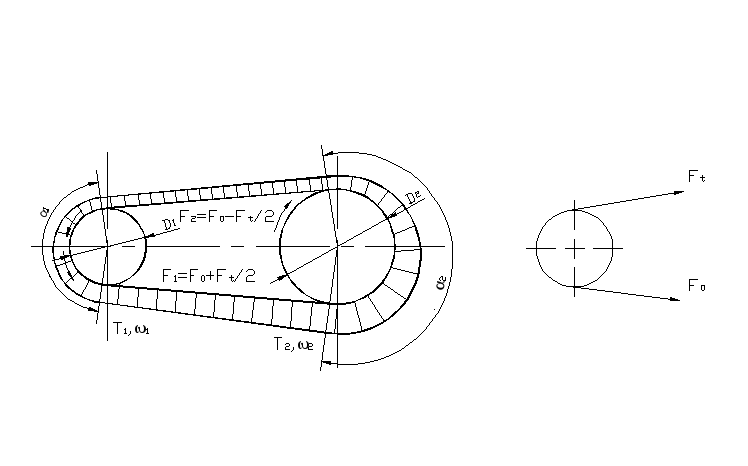
Рисунок 2 – Силовая схема передачи гибкой связью

Изменение усилия вызывает проскальзывания гибкой связи по шкивам, поскольку деформация ремня зависит от величины передаваемой им нагрузки. С учетом соотношения ремня по шкивам передаточное отношение определяют по (2). Для таких передач 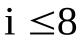, для приборных передач ввиду малого передаточного момента передаточное отношение может доходить до .

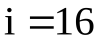В качестве гибкой связи используют плоский или клиновый ремень, шнуры из шелка, капрона, резины, пластмасс, стальные тросики, а также ленту.

Шкивы изготавливают из стали, легких сплавов и пластмасс. Наименьший размер шкива в кинематических передачах D_1min= 6 – 8 мм. Угол обхвата ведущего шкива 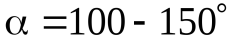; для увеличения угла обхвата и силы натяжения гибкой связи применяют натяжные ролики.

7.Зубчатые передачи в мехатронных модулях и принципы их проектирования.

Зубчатая передача – это механизм, который с помощью зубчатого зацепления передает или преобразует движение с изменением угловых скоростей и моментов. Зубчатая передача состоит из колес с зубьями, которые сцепляются между собой, образуя ряд последовательно работающих кулачковых механизмов.

Зубчатые передачи применяют для преобразования и передачи вращательного движения между валами с параллельными, пересекающимися или перекрещивающимися осями, а также для преобразования вращательного движения в поступательное и наоборот.

Достоинства зубчатых передач:

1.Постоянство передаточного отношения i.

2.Надежность и долговечность работы.

3.Компактность.

4.Большой диапазон передаваемых скоростей.

5.Небольшое давление на валы.

6.Высокий КПД.

7.Простота обслуживания.

Недостатки зубчатых передач:

1.Необходимость высокой точности изготовления и монтажа.

2.Шум при работе со значительными скоростями.

3.Невозможность бесступенчатого регулирования передаточного отно-

шения i.

Зубчатые передачи, применяемые в механических системах, разнообразны. Они используются как для понижения, так и для повышения угловой скорости.

Классификация конструкций зубчатых преобразователей группирует передачи по трем признакам:

1. По виду зацепления зубьев. В технических устройствах применяются передачи с внешним, с внутренним и с реечным зацеплением.

Передачи с внешним зацеплением применяются для преобразования вращательного движения с изменением направления движения.

Внутреннее зацепление применяется в том случае, если требуется преобразовывать вращательное движение с сохранением направления.

Реечное зацепление применяется при преобразовании вращательного движения в поступательное и обратно.

2. По взаимному расположению осей валов различают передачи цилиндрическими колесами с параллельными осями валов, коническими колесами с пересекающимися осями, колесами со скрещивающимися осями.

Передачи c коническими колесами обладают меньшим передаточным отношением, более сложны в изготовлении и эксплуатации, имеют дополнительные осевые нагрузки. Винтовые колеса работают с повышенным скольжением, быстрее изнашиваются, имеют малую нагрузочную способность. Эти передачи могут обеспечивать различные передаточные отношения при одинаковых диаметрах колес.

3. По расположению зубьев относительно образующей обода колеса различают передачи прямозубые, косозубые, шевронные и с круговыми зубьями.

8.Волновые приводы в мехатронных модулях и основы их конструирования.

Волновой привод предназначен для повышения быстродействия за счет снижения момента инерции генератора волн. Волновая передача с неподвижным гибким колесом установлена в корпусе. Жесткое колесо и генератор волн установлены на валу привода. По меньшей мере один электродвигатель установлен на плате и размещен между корпусом и гибким колесом и связан с зубчатым венцом генератора волны через по крайней мере один промежуточный вал с двумя венцами. Вал электродвигателя обращен в противоположную от генератора волн сторону. В плате выполнен вырез под гибкое колесо, а в гибком колесе - под промежуточный вал. 1 з.п. ф-лы, 2 ил.

Изобретение относится к деталям машин и может быть использовано в составе изделий авиационной и ракетной техники.

Известен волновой привод, содержащий корпус, размещенные в нем электродвигатель и волновую передачу, а также промежуточный редуктор между валом электродвигателя и генератором волны [1]. Недостатком этой волновой передачи являются значительные осевые габариты, что вызвано установкой подшипников выходного вала с одной стороны генератора волн.

Этого недостатка лишен волновой привод, выбранный в качестве прототипа, содержащий корпус с крышкой, установленные в нем волновую передачу с неподвижным гибким колесом и жестким колесом, размещенным на валу привода, плату с по меньшей мере одним электродвигателем, выходной вал которого через редуктор связан с генератором волн волновой передачи, установленным на валу привода на подшипниках [2]. Установка подшипников выходного вала по разные стороны генератора волн позволяет существенно снизить осевые габариты.

Недостатком такого волнового привода является низкое быстродействие и значительные осевые габариты. Низкое быстродействие обусловлено тем, что диаметр гибкого колеса в прототипе обусловлен необходимостью размещения внутри него платы с электродвигателями и выбран большим, чем это требуются расчетом гибкого колеса на прочность [3], что влечет за собой увеличение диаметра кулачка генератора волн и, соответственно, его момента инерции. Осевые габариты прототипа из-за его конструктивной схемы также значительны, что объясняется последовательным расположением в осевом направлении электродвигателей и генератора волн.

Техническим результатом, достигаемым с помощью предлагаемого изобретения, является повышение быстродействия за счет снижения момента инерции генератора волн и снижение осевых габаритов.

Этот результат достигается за счет того, что в известном волновом приводе, содержащем корпус с крышкой, установленные в нем волновую передачу с неподвижным гибким колесом и жестким колесом, размещенным на валу привода, плату с электродвигателем, вал которого через редуктор связан с генератором волн волновой передачи, установленным на валу привода на подшипниках, согласно изобретению электродвигатель размещен между корпусом и гибким колесом и связан с зубчатым венцом генератора волн через по крайней мере один промежуточный вал с двумя зубчатыми венцами, вал с двумя зубчатыми венцами, вал электродвигателя обращен в противоположную от генератора волн сторону, а в плате выполнен вырез под гибкое колесо. При этом при использовании одного промежуточного вала в гибком колесе выполнен вырез под этот промежуточный вал. Такая совокупность признаков позволяет снизить диаметр и длину гибкого колеса, вследствие чего снижается диаметр и, соответственно, момент инерции генератора волн, что повышает быстродействие привода. Также снижаются осевые габариты привода.

На фиг. 1 приведен пример конкретного выполнения волнового привода, продольный разрез; на фиг. 2 - то же, вид слева (крышка корпуса не показана).

Волновой привод содержит корпус 1 с крышкой 2, установленные в нем на подшипниках 3 выходной вал 4, плату 5 с электродвигателем 6 и волновую передачу с неподвижным гибким колесом 7 и жестким колесом 8, размещенным на валу 4 и соединенным с ним штифтовым соединением. На валу 4 в подшипниках 9 установлен генератор волн 10. На плате 5 в подшипниках 11 размещен промежуточный вал 12 с зубчатыми венцами 13 и 14. Венец 13 находится в зацеплении с шестерней 15, установленной на валу электродвигателя 6, а венец 14 - в зацеплении с венцом 16, выполненном на кулачке генератора волн 10. Шестерня 15, промежуточный вал 12 с венцами 13 и 14, а также венец 16 являются редуктором, через который вал электродвигателя 6 связан с генератором волн 10. В гибком колесе 7 выполнен вырез 17 под промежуточный вал, при этом в плате 5 выполнен вырез 18 под гибкое колесо 7. Электродвигатель 6 размещен между корпусом 1 и гибким колесом 7, вал электродвигателя обращен в противоположную от генератора волн сторону. Гибкое колесо 7 зафиксировано в крышке 2 штифтами 19.

Волновой привод работает следующим образом.

При включении электродвигателя 6 вращение его ротора через редуктор, образованный шестерней 15, венцами 13 и 14 вала 12 и венцом 16, передается на генератор волн 10. Генератор волн 10 деформирует гибкое колесо 7 и приводит жесткое колесо 8 и вал 4 во вращение в подшипниках 3. Наличие выреза 17 в гибком колесе обеспечивает передачу момента от вала электродвигателя 6 к генератору волн 10 и не влияет на работу волновой передачи, так как находится вне зоны зацепления гибкого колеса с жестким. Использование таких вырезов известно в литературе [4]. Размещение электродвигателя вне гибкого колеса позволяет снизить диаметр и длину гибкого колесо до размеров, необходимых по прочностному расчету (приблизительно в 1,5 раза). Соответственно уменьшается масса и момент инерции генератора волн. При условии сохранения осевых размеров генератора волн неизменными, снижение момента инерции будет приблизительно пропорционально третьей степени снижения наружного диаметра генератора волн (так как момент инерции пропорционален первой степени массы и квадрату диаметра), т.е. в 3,3 раза. Соответственно в таком же размере повышается и быстродействие привода. Кроме того, подобное расположение электродвигателя позволяет снизить осевую длину привода до длины, равной длине электродвигателя плюс толщина двух стенок привода (в прототипе эта длина была больше вышеприведенной на толщину генератора волн и стенки жесткого колеса), т. е. снизить ее на 20 - 25%. Для изделий авиационной и ракетной техники подобное снижение одного измерения весьма существенно, так как эти изделия характеризуются значительной боковой поверхностью и длиной при относительно малом диаметре, что задает весьма жесткие требования к осевой длине агрегатов при их размещении перпендикулярно боковой поверхности изделия. Существенным для реализации изобретения является наличие только одного электродвигателя, но могут быть использованы и несколько электродвигателей, передающих момент через промежуточные валы на венец 16. Их расположение полностью аналогично расположению электродвигателя 6 и промежуточного вала 12, поэтому они не изображены на чертежах. Однако в формуле изобретения это нашло отражение в обобщающем признаке "плата с по меньшей мере одним электродвигателем". Вращение от электродвигателя может передаваться на генератор волн и через несколько промежуточных валов (при необходимости обеспечить большее передаточное отношение), однако существенным для реализации изобретения является наличие только одного промежуточного вала. Указанные дополнительные валы могут быть также размещены между корпусом и гибким колесом. Таким образом, предлагаемое техническое решение позволяет существенно повысить быстродействие привода и снизить его осевые габариты, что расширяет возможности компоновки привода в малых объемах.

9.Шарико-винтовые передачи в мехатронных модулях и принципы их конструирования.

Шарико-винтовая передача (ШВП) – это линейный механический привод, преобразующий вращение в линейное перемещение и наоборот. Конструктивно она представляет собой длинный винт, по которому движется шариковая гайка. Внутри гайки между ее внутренней резьбой и резьбой винта по спиралевидной траектории катятся шарики, затем попадая в возвратные каналы – внутренние или внешние.

Концы винта обычно закрепляются на подшипниковых опорах, а гайка соединена с перемещаемым узлом. Когда винт вращается, гайка линейно перемещается по винту вместе с полезной нагрузкой. Но существуют и шарико-винтовые пары с вращающейся гайкой – в такой конструкции винт линейно перемещается относительно гайки.

ШВП значительные преимущества:

КПД может превышать 80%

требуемые мощность и крутящий момент приводных двигателей намного меньше

интенсивность износа минимизирована

срок службы намного больше, чем у винтовых передач скольжения, и может быть определен вычислением усталости при качении

меньший нагрев способствует непрерывной работе

Существуют два типа шарико-винтовых передач, различающихся технологией изготовления резьбового винта: катаные (накатка резьбы) и шлифованные (нарезка резьбы с последующей шлифовкой поверхности). Катаные винты проще в производстве, поэтому более доступны. Шлифованные дороже, но имеют значительно лучшую точность изготовления резьбы, а, следовательно, точность и повторяемость позиционирования. Важным параметром также является шаг резьбы. Чем он больше, тем выше максимальная линейная скорость, но ниже точность позиционирования и осевое усилие.

10.Конструирование мехатронных модулей с заданной точностью перемещения.

11.Анализ потери устойчивости.

Трефилов

Локационные системы в МиР

Методы и теория оптимизации

1.Методы оптимизации. Основные понятия.

Оптимизация - процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т. п.

В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу. При решении инженерных задач их принято называть проектными параметрами, а в экономических задачах их обычно называют параметрами плана. В качестве проектных параметров могут быть, в частности, значения линейных размеров объекта, массы, температуры и т. п. Число п проектных параметров x₁,x₂,…,x_п характеризует размерность (и степень сложности) задачи оптимизации.

Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией (или критерием качества). В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум). Таким образом, целевая функция — это глобальный критерий оптимальности в математических моделях, с помощью которых описываются инженерные или экономические задачи.

Целевую функцию можно записать в виде

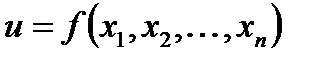
(6.1)

Примерами целевой функции, встречающимися в инженерных и экономических расчетах, являются прочность или масса конструкции, мощность установки, объем выпуска продукции, стоимость перевозок грузов, прибыль и т. п.

В случае одного проектного параметра (n = 1) целевая функция (6.1) является функцией одной переменной, и ее график — некоторая кривая на плоскости. При n = 2 целевая функция является функцией двух переменных, и ее график — поверхность в трехмерном пространстве.

Следует отметить, что целевая функция не всегда может быть представлена в виде формулы. Иногда она может принимать только некоторые дискретные значения, задаваться в виде таблицы и т. п. Во всех случаях она должна быть однозначной функцией проектных параметров.

Целевых функций может быть несколько. Например, при проектировании изделий машиностроения одновременно требуется обеспечить максимальную надежность, минимальную материалоемкость, максимальный полезный объем (или грузоподъемность). Некоторые целевые функции могут оказаться несовместимыми. В таких случаях необходимо вводить приоритет той или иной целевой функции.
Экстремум без ограничений.

Пусть f: RⁿàR- функция n действительных переменных, обладающая некоторой гладкостью(определенная деференцируемость функции). fϵD^k(ẋ)- функция f дифференцируема к –раз в точке ẋ.

f(х)àextr- гладкая конечномерная задача без ограничений.

При решении задачи надо найти абсолютные и локальные экстремумы.

Точка ẋ- точка локального минимума(максимума) функции f, если существует окрестность

Uᶓ={x

X- ẋ |<ᶓ} точки ẋ такая, что f(x)≥f(ẋ) (f(x)≤f(ẋ))для любой точки x для этой окрестности. Пишем, когда речь идет о минимуме и максимуме - ẋϵlocextrf. Теорема 1(Ферма). Пустьf: R --->R- функция одного действительного переменного. Если ẋϵlocextrf- точка локального экстремума функции f и функция fϵD(ẋ) дифференцируема в точке ẋ, то f”(ẋ)=0- это условие стационарности или необходимое условие экстремума 1 порядка. Точки, удовлетворяющие условию стационарности, называются стационарными. Доказательство. По определению дифференцируемости функции f(ẋ+h)=f(ẋ)+f’(ẋ)h+r(h), r(h)=o(h)=o(1)h при малыхh. Значит ,f(ẋ+h)-f(ẋ)=(f’(ẋ)+o(1))h. Если бы f’(ẋ)≠0, то при hдостаточно близких к нулю , величина f’(ẋ)+o(1) имела бы знакf’(ẋ), посколькуo(1)-à0 приhà0.Само жеh может принимать как «+» так и «-» значения. Следовательно , разность f(ẋ +h)-f(ẋ) может быть как меньше, так и больше 0. Геометрически теорема Ферма дает необходимое условие 1 порядка для существоания локального экстремума. Экстремумы функций с ограничением в виде равенств. Пустьfi: Rn-àR, i=0,1,…,m,- функции n переменных, отображающие равенство Rn в R . Все функции fi обладают определенной гладкостью. Гладкой конечномерной задачей с ограничениями типа равенств называется f0(x)àextr; fi(x)=0, i=1,…,m. Т.о. в задаче (P) ищутся экстремумы функции на множестве, задаваемом конечным числом ограничений типа равенств.Точки удовлетворяющие ограничениям типа равенств, называются допустимыми точками в задаче. Необходимые и достаточные условия эстремума Принцип Лагранжа Для решения задачи с ограничениями типа равенств составляется функция Лагранжа. Функционал ,экстремум которого ищется , умножается на множитель λ0, функции ограничений fi(x)=0 умножаются на множители соответственно λi, складываются и выписывются функция Лагранжа L(x)= . Необходимые условия экстремума в задаче с ограничениями выписываются через необходимые условия экстремумы функции Лагранжа. Вектор называется вектором множителей Лагража. 2.Метод множителей Лагранжа для функций двух переменных. Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: F(x,y)=f(x,y)+λφ(x,y) (параметр λ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки: Достаточным условием, из которого можно выяснить характер экстремума, служит знак d2F=F′′xxdx2+2F′′xydxdy+F′′yydy2. Если в стационарной точке d2F>0, то функция z=f(x,y) имеет в данной точке условный минимум, если же d2F<0, то условный максимум. Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: φ′xdx+φ′ydy=0, dy=−φ′xφ′ydx, поэтому в любой стационарной точке имеем: d2F=F′′xxdx2+2F′′xydxdy+F′′yydy2=F′′xxdx2+2F′′xydx(−φ′xφ′ydx)+F′′yy(−φ′xφ′ydx)2==−dx2(φ′y)2⋅(−(φ′y)2F′′xx+2φ′xφ′yF′′xy−(φ′x)2F′′yy) Второй сомножитель (расположенный в скобке) можно представить в такой форме: Красным цветом выделены элементы определителя , который является гессианом функции Лагранжа. Если H>0, то d2F<0, что указывает на условный максимум. Аналогично, при H<0 имеем d2F>0, т.е. имеем условный минимум функции z=f(x,y). Метод множителей Лагранжа для функций n переменных Допустим, мы имеем функцию n переменных z=f(x1,x2,…,xn) и m уравнений связи (n>m): φ1(x1,x2,…,xn)=0;φ2(x1,x2,…,xn)=0,…,φm(x1,x2,…,xn)=0. Обозначив множители Лагранжа как λ1,λ2,…,λm, составим функцию Лагранжа: F(x1,x2,…,xn,λ1,λ2,…,λm)=f+λ1φ1+λ2φ2+…+λmφm Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа: Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака d2F. Если в найденной точке d2F>0, то функция имеет условный минимум, если жеd2F<0, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу: Определитель матрицы, выделенной в матрице L красным цветом, есть гессиан функции Лагранжа. Используем следующее правило: Если знаки угловых миноров H2m+1,H2m+2,…,Hm+n матрицы L совпадают с знаком (−1)m, то исследуемая стационарная точка является точкой условного минимума функции z=f(x1,x2,x3,…,xn). Если знаки угловых миноров H2m+1,H2m+2,…,Hm+n чередуются, причём знак минора H2m+1совпадает с знаком числа (−1)m+1, то исследуемая стационарная точка является точкой условного максимума функции z=f(x1,x2,x3,…,xn). 3. Методы оптимизации. Линейное программирование. Линейное программирование представляет собой математический аппарат, разработанный для решения оптимальных задач с линейными выражениями для критерия оптимальности и линейными ограничениями на область изменения переменных. Такие задачи обычно встречаются при решении вопросов оптимального планирования производства с ограниченным количеством ресурсов, при определении оптимального плана перевозок (транспортные задачи) и т. д. Для решения большого круга задач линейного программирования имеется практически универсальный алгоритм - симплексный метод, позволяющий за конечное число итераций находить оптимальное решение подавляющего большинства задач. Тип используемых ограничений (равенства или неравенства) не сказывается на возможности применения указанного алгоритма. Общей (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида[3]: Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП) , . Задача линейного программирования будет иметь канонический вид, если в общей задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства[4]: , Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит в следующем: 1) умение находить начальный опорный план; 2) наличие признака оптимальности опорного плана; 3) умение переходить к нехудшему опорному плану. С каждой задачей ЛП тесно связана другая линейная задача, называемая двойственной. Решение одной задачи двойственной пары может быть получено из решения другой. Переменные двойственной задачи называют объективно обусловленными оценками, ценами ресурсов, теневыми ценами. Использование двойственного симплекс-метода для решения задач линейного программирования обусловлено его возможностью находить допустимые и оптимальные планы в условиях, когда прямой симплекс-метод не может быть использован. Двойственный симплекс-метод использует видоизмененные условия допустимости и оптимальности, что обеспечивает ему продвижение к общему с прямой задачей решению с внешней стороны многоугольника ограничений. 4. Методы оптимизации. Нелинейное программирование. Последовательное квадратичное программирование(SQP) — один из наиболее распространённых и эффективных оптимизационных алгоритмов общего назначения, основной идеей которого является последовательное решение задач квадратичного программирования, аппроксимирующих данную задачу оптимизации. Для оптимизационных задач без ограничений алгоритм SQP преобразуется в метод Ньютона поиска точки, в которой градиент целевой функции обращается в ноль. Для решения исходной задачи с ограничениями-равенствами метод SQP преобразуется в специальную реализацию ньютоновских методов решения системы Лагранжа. Рассмотрим задачу нелинейного программирования следующего вида: при ограничениях Лагранжиан задачи примет следующий вид: где и — множители Лагранжа. На итерации основного алгоритма определяются соответствующие направления поиска как решение следующей подзадачи квадратичного программирования: при ограничениях Подобное решение уравнений Куна-Таккера служит основой для большинства алгоритмов нелинейного программирования. В этих алгоритмах часто используется прямое вычисление множителей Лагранжа. Квазиньютоновские методы обеспечивают сверхлинейную сходимость путем накопления информации второго порядка относительно уравнений Куна-Таккера, использующих процедуры квазиньютоновской корректировки. В общем случае эти методы можно отнести к задачам Последовательного квадратичного программирования (SQP), поскольку проблема QP решается на каждой главной итерации 5.Численные методы безусловной оптимизации нулевого порядка Основные определения Решение многих теоретических и практических задач сводится к отысканию экстремума (наибольшего или наименьшего значения) скалярной функции f(х) n-мерного векторного аргументах. В дальнейшем под x будем понимать вектор-столбец (точку в n-мерном пространстве): Вектор-строка получается путем применения операции транспонирования: . Оптимизируемую функцию f(x) называют целевой функцией или критерием оптимальности. В дальнейшем без ограничения общности будем говорить о поиске минимального значения функции f(x) записывать эту задачу следующим образом: f(x ) --> min. Вектор х*, определяющий минимум целевой функции, называют оптимальным. Отметим, что задачу максимизации f(x) можно заменить эквивалентной ей задачей минимизации или наоборот. Рассмотрим это на примере функции одной переменной (Рис. 2.1). Если х* - точка минимума функции y = f(x), то для функции y =- f(x) она является точкой максимума, так как графики функций f(x) и - f(x), симметричны относительно оси абсцисс. Итак, минимум функции f(x) и максимум функции - f(x) достигаются при одном и том же значении переменной. Минимальное же значение функции f(x), равно максимальному значению функции - f(x), взятому с противоположным знаком, т.е. min f(x) =-max(f(x)). Рассуждая аналогично, этот вывод нетрудно распространить на случай функции многих переменных. Если требуется заменить задачу минимизации функции f(x1, …, xn) задачей максимизации, то достаточно вместо отыскания минимума этой функции найти максимум функции f(x1, …, xn). Экстремальные значения этих функций достигаются при одних и тех же значениях переменных. Минимальное значение функции f(x1, …, xn) равно максимальному значению функции - f(x1, …, xn), взятому с обратным знаком, т.е. min f(x1, …, xn) =max f(x1, …, xn). Отмеченный факт позволяет в дальнейшем говорить только о задаче минимизации. Рис. 2.1. Экстремум В реальных условиях на переменные xj, i=1, …. n, и некоторые функции gi (х), hi(х), характеризующие качественные свойства объекта, системы, процесса, могут быть наложены ограничения (условия) вида: gi (х) = 0, i=1, …. n, hi (х) <= 0, i=1, …. n, a <= x <= b, где ; Такую задачу называют задачей условной оптимизации. При отсутствии ограничений имеет место задача безусловной оптимизации. Каждая точка х в n-мерном пространстве переменных х1, …, хn, в которой выполняются ограничения, называется допустимой точкой задачи. Множество всех допустимых точек называют допустимой областью G. Решением задачи (оптимальной точкой)называют допустимую точку х*, в которой целевая функция f(х) достигает своего минимального значения. Точка х* определяет глобальный минимум функции одной переменной f(x), заданной на числовой прямой Х , если x * X иf(x*) < f(x) для всех x* X (Рис. 2.2, а). Точка х* называется точкой строгого глобального минимума, если это неравенство выполняется как строгое. Если же в выражении f(х*) <= f(x) равенство возможно при х, не равных х*, то реализуетсянестрогий минимум, а под решением в этом случае понимают множество х* = [x* X: f(x) = f(x*)] (Рис. 2.2, б). Рис. 2.2. Глобальный минимум. а - строгий, б - нестрогий Точка х* Х определяет локальный минимум функции f(x) на множестве Х , если при некотором достаточно малом e > 0 для всех х, не равных х*, x X, удовлетворяющих условию ¦х - х*¦<= e, выполняется неравенство f(х*) < f(х). Если неравенство строгое, то х* является точкой строгого локального минимума. Все определения для максимума функции получаются заменой знаков предыдущих неравенств на обратные. На Рис. 2.3 показаны экстремумы функции одной переменной f(х) на отрезке [a, b] . Здесь х1, х3, х6 - точки локального максимума, а х2, х4 - локального минимума. В точке х6реализуется глобальный максимум, а в точке х2 - глобальный минимум. Рис. 2.3. Экстремумы функции Классификация методов Возможны два подхода к решению задачи отыскания минимума функции многих переменных f(x) = f(x1, ..., хn) при отсутствии ограничений на диапазон изменения неизвестных. Первый подход лежит в основе косвенных методов оптимизации и сводит решение задачи оптимизации к решению системы нелинейных уравнений, являющихся следствием условий экстремума функции многих переменных. Как известно, эти условия определяют, что в точке экстремума х* все первые производные функции по независимым переменным равны нулю: , i=1, …, n. Эти условия образуют систему п нелинейных уравнений, среди решений которой находятся точки минимума. Вектор f’(х), составленный из первых производных функции по каждой переменной, т.е. , называют градиентом скалярной функции f(x). Как видно, в точке минимума градиент равен нулю. Решение систем нелинейных уравнений - задача весьма сложная и трудоемкая. Вследствие этого на практике используют второй подход к минимизации функций, составляющий основу прямых методов. Суть их состоит в построении последовательности векторов х [0], х [1], …, х [n], таких, что f(х[0])> f(х [1])> f(х [n])>… В качестве начальной точки x[0] может быть выбрана произвольная точка, однако стремятся использовать всю имеющуюся информацию о поведении функцииf(x), чтобы точка x[0] располагалась как можно ближе к точке минимума. Переход (итерация) от точки х [k] к точке х [k+1], k= 0, 1, 2, ..., состоит из двух этапов: выбор направления движения из точки х [k]; определение шага вдоль этого направления. Методы построения таких последовательностей часто называют методами спуска, так как осуществляется переход от больших значений функций к меньшим. Математически методы спуска описываются соотношением x[k+1] = x[k] + akp[k], k = 0, 1, 2, ..., где p[k] - вектор, определяющий направление спуска; ak - длина шага. В координатной форме: Различные методы спуска отличаются друг от друга способами выбора двух параметров - направления спуска и длины шага вдоль этого направления. На практике применяются только методы, обладающие сходимостью. Они позволяют за конечное число шагов получить точку минимума или подойти к точке, достаточно близкой к точке минимума. Качество сходящихся итерационных методов оценивают по скорости сходимости. В методах спуска решение задачи теоретически получается за бесконечное число итераций. На практике вычисления прекращаются при выполнении некоторых критериев (условий) останова итерационного процесса. Например, это может быть условие малости приращения аргумента или функции . Здесь k - номер итерации; e, g - заданные величины точности решения задачи. Методы поиска точки минимума называются детерминированными, если оба элемента перехода от х[k] к x[k+l] (направление движения и величина шага) выбираются однозначно по доступной в точке х [k] информации. Если же при переходе используется какой-либо случайный механизм, то алгоритм поиска называется случайным поиском минимума. Детерминированные алгоритмы безусловной минимизации делят на классы в зависимости от вида используемой информации. Если на каждой итерации используются лишь значения минимизируемых функций, то метод называется методом нулевого порядка. Если, кроме того, требуется вычисление первых производных минимизируемой функции, то имеют место методыпервого порядка, при необходимости дополнительного вычисления вторых производных - методы второго порядка. В настоящее время разработано множество численных методов для задач как безусловной, так и условной оптимизации. Естественным является стремление выбрать для решения конкретной задачи наилучший метод, позволяющий за наименьшее время использования ЭВМ получить решение с заданной точностью. Качество численного метода характеризуется многими факторами: скоростью сходимости, временем выполнения одной итерации, объемом памяти ЭВМ, необходимым для реализации метода, классом решаемых задач и т. д. Решаемые задачи также весьма разнообразны: они могут иметь высокую и малую размерность, быть унимодальными (обладающими одним экстремумом) и многоэкстремальными и т. д. Один и тот же метод, эффективный для решения задач одного типа, может оказаться совершенно неприемлемым для задач другого типа. Очевидно, что разумное сочетание разнообразных методов, учет их свойств позволят с наибольшей эффективностью решать поставленные задачи. Многометодный способ решения весьма удобен в диалоговом режиме работы с ЭВМ. Для успешной работы в таком режиме очень полезно знать основные свойства, специфику методов оптимизации. Это обеспечивает способность правильно ориентироваться в различных ситуациях, возникающих в процессе расчетов, и наилучшим образом решить задачу. Метод прямого поиска (Хука-Дживса).(из учебника) Суть этого метода состоит в следующем. Задаются некоторой начальной точкой х[0]. Изменяя компоненты вектора х[0], обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции f(x). В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д. Алгоритм метода прямого поиска состоит в следующем. 1. Задаются значениями координат хi[0] , i = 1, ..., п , начальной точки х[0], вектором изменения координат х в процессе обследования окрестности, наименьшим допустимым значением е компонентов х. 2. Полагают, что х[0] является базисной точкой хб, и вычисляют значение f(xб). 3. Циклически изменяют каждую координату хбi, i = 1, ..., п , базисной точки хб на величину ?хi, i = 1, ...,п , т. е. хi[k] = хб +  х; хi[k] = хбi - ?хi. При этом вычисляют значения f(x[k]) и сравнивают их со значением f(xб). Если f(x[k]) < f(xб), то соответствующая координата хi, i = 1, ..., п , приобретает новое значение, вычисленное по одному из приведенных выражений. В противном случае значение этой координаты остается неизменным. Если после изменения последней п-й координаты f(x[k]) < f(xб), то переходят к п, 4. В противном случае - к п. 7. 4. Полагают, что х[k] является новой базисной точкой хб , и вычисляют значение f(xб). 5. Осуществляют спуск из точки х[k] > хi[k+1] = 2хi[k] - xб , i = 1, ..., n , где xб - координаты предыдущей базисной точки. Вычисляют значение f(x[k+1]). 6. Как и в п. 3, циклически изменяют каждую координату точки х[k+1], осуществляя сравнение соответствующих значений функции f(х) со значением f (х[k+1]), полученным в п. 5. После изменения последней координаты сравнивают соответствующее значение функции f(x[k]) со значением f(xб),полученным в п. 4. Если f(x[k]) < f(xб), то переходят к п. 4, в противном случае - к п. 3. При этом в качестве базисной используют последнюю из полученных базисных точек. 7. Сравнивают значения  х и е. Если  х < е, то вычисления прекращаются. В противном случае уменьшают значения  х и переходят к п. 3. Достоинством метода прямого поиска является простота его программирования на компьютере. Он не требует знания целевой функции в явном виде, а также легко учитывает ограничения на отдельные переменные, а также сложные ограничения на область поиска. Недостаток метода прямого поиска состоит в том, что в случае сильно вытянутых, изогнутых или обладающих острыми углами линий уровня целевой функции он может оказаться неспособным обеспечить продвижение к точке минимума. Действительно, в случаях, изображенных на Рис. 2.4, а и б, каким бы малым ни брать шаг в направлении х1 или x2 из точки х’ нельзя получить уменьшения значения целевой функции. Рис. 2.4. Прямой поиск: невозможность продвижения к минимуму: а – С1 > C2 > C3; б - С1 > C2 Напомним, что поверхностью уровня (на плоскости - линией уровня) является поверхность, получаемая приравниванием выражения функции f(х) некоторой постоянной величине С, т. е. f(х) = С . Во всех точках этой поверхности функция имеет одно и то же значение С. Давая величине С различные значенияС1, ..., Сn, получают ряд поверхностей, геометрически иллюстрирующих характер функции. 6.Метод деформируемого многогранника (метод Нелдера—Мида) Данный метод состоит в том, что для минимизации функции n переменных f(х) в n-мерном пространстве строится многогранник, содержащий (n + 1) вершину.Соответственно, треугольник для плоскости и тетраэдр для 3-мерного пространства. Очевидно, что каждая вершина соответствует некоторому вектору х. Вычисляются значения целевой функции f(х) в каждой из вершин многогранника, определяются максимальное из этих значений и соответствующая ему вершина х[h]. Через эту вершину и центр тяжести остальных вершин проводится проецирующая прямая, на которой находится точка х[q] с меньшим значением целевой функции, чем в вершине х[h] (Рис. 2.5). Затем исключается вершина х[h].Из оставшихся вершин и точки x[q] строится новый многогранник, с которым повторяется описанная процедура. В процессе выполнения данных операций многогранник изменяет свои размеры, что и обусловило название метода. Рис. 2.5. Геометрическая интерпретация метода деформируемого многогранника Введем следующие обозначения: x[i, k] =(x1[i, k], …, xj[i, k], …, xn[i, k])T где i = 1, ..., n + 1; k = 0, 1, ..., - i-я вершина многогранника на k-м этапе поиска; х[h, k] — вершина, в которой значение целевой функции максимально, т. е. f(х[h, k]) = max{f(x[1, k]), …, f(x[n+1, k])}; х[l, k] -вершина, в которой значение целевой функции минимально, т. е. f(х[l, k]) =min{f(x[1, k]), …, f(x[n+1, k])}; х[n+2, k]- центр тяжести всех вершин, за исключениемх[h, k]. Координаты центра тяжести вычисляются по формуле Параметрами метода являются: коэффициент отражения alpha{\displaystyle \alpha >0}ффффффa, обычно выбирается равным {\displaystyle 1}1. коэффициент сжатия {\displaystyle \beta >0}beta, обычно выбирается равным {\displaystyle 0{,}5}0,5. коэффициент растяжения gamma{\displaystyle \gamma >0}, обычно выбирается равным 2{\displaystyle 2}. Алгоритм метода деформируемого многогранника состоит в следующем: 1. Вычисляются значения целевой функции f(х) в каждой из вершин многогранника, определяются максимальное из этих значений и соответствующая ему вершина х[h]. Через эту вершину и центр тяжести остальных вершин проводится проецирующая прямая, на которой находится точка х[q] с меньшим значением целевой функции, чем в вершине х[h]. 2. Осуществляют проецирование точки х[h, k] через центр тяжести: x[n+3, k] =x[n+2, k] + a(x[n+2, k] - x[h, k]) , где а > 0 - некоторая константа. Обычно а = 1. 3. Выполняют операцию растяжения вектора х[n+3, k] - х[n+2, k]: x[n+4, k] =x[n+2, k] + g(x[n+3, k] - x[n+2, k]), где g >1 - коэффициент растяжения. Наиболее удовлетворительные результаты получают при 2,8 <= g <= 3. Если f(x[n+4, k]) < f(х[l, k]), то х[h , k] заменяют на x[n+4, k] и продолжают вычисления с п. 1 при k = k + 1. В противном случае х[h, k] заменяют на х[n+3, k] и переходят к п. 1 при k = k + 1. 4. Если f(x[n+3, k]) > f(х[i, k]) для всех i, не равных h, то сжимают вектор x[h, k] - x[n+2, k]: x[n+5, k] =x[n+2, k] + b (х[h, k] – x[n+2, k] ), где b > 0 - коэффициент сжатия. Наиболее хорошие результаты получают при 0,4 <= b <= 0,6. Затем точку х[h, k] заменяют на х[n+5, k] и переходят к п. 1 при k = k+ 1. 5. Если f(x[n+3, k])> f(x[h, k]), то все векторы х[i, k] - х[l, k] . i= 1,..., п + 1, уменьшают в два раза: x[i, k] = x[l, k] + 0,5(x[i, k] - x[l, k]) . Затем переходят к п. 1 при k= k + 1. В диалоговой системе оптимизации выход из подпрограммы, реализующей метод деформируемого многогранника, осуществляется при предельном сжатии многогранника, т. е. при выполнении условия , где e = (е1 ,..., еn) - заданный вектор. С помощью операции растяжения и сжатия размеры и форма деформируемого многогранника адаптируются к топографии целевой функции. В результате многогранник вытягивается вдоль длинных наклонных поверхностей, изменяет направление в изогнутых впадинах, сжимается в окрестности минимума, что определяет эффективность рассмотренного метода. 7.Метод вращающихся координат (метод Розенброка) Суть метода состоит во вращении системы координат в соответствии с изменением скорости убывания целевой функции. Новые направления координатных осей определяются таким образом, чтобы одна из них соответствовала направлению наиболее быстрого убывания целевой функции, а остальные находятся из условия ортогональности. Идея метода состоит в следующем (Рис. 2.6). Рис. 2.6. Геометрическая интерпретация метода Розенброка Из начальной точки х[0] осуществляют спуск в точку х[1] по направлениям, параллельным координатным осям. На следующей итерации одна из осей должна проходить в направлении y1 = х[1] - х[0], а другая - в направлении, перпендикулярном к у1 . Спуск вдоль этих осей приводит в точку х[2] , что дает возможность построить новый вектор х[2] - х[1] и на его базе новую систему направлений поиска. В общем случае данный метод эффективен при минимизации овражных функций, так как результирующее направление поиска стремится расположиться вдоль оси оврага. Алгоритм метода вращающихся координат состоит в следующем. 1. Обозначают через р1[k], ..., рn[k] направления координатных осей в некоторой точке х[k] (на к-й итерации). Выполняют пробный шаг h1 вдоль оси р1[k], т. е. x[kl] = x[k] + h1p1[k]. Если при этом f(x[kl]) < f(x[k]), то шаг h умножают на величину b > 1; Если f(x[kl]) > f(x[k]), - то на величину (-b), 0 < |b| < 1; x[kl] = x[k] + b h1p1[k]. Полагая ?h1 = а1 .получают x[kl] = x[k] + a1p1[k]. 2. Из точки х[k1] выполняют шаг h2 вдоль оси р2[k]: x[k2] = x[k] + a1p1[k] + h2p2[k]. Повторяют операцию п. 1, т. е. x[k2] =x[k] + а1р1[k] +а2p2[k]. Эту процедуру выполняют для всех остальных координатных осей. На последнем шаге получают точку . 3. Выбирают новые оси координат p1[k+1], …, рn[k+1]. В качестве первой оси принимается вектор р1[k+1] = x[k+l] - x[k]. Остальные оси строят ортогональными к первой оси с помощью процедуры ортогонализации Грама - Шмидта. Повторяют вычисления с п. 1 до удовлетворения условий сходимости. Коэффициенты b подбираются эмпирически. Хорошие результаты дают значения b = - 0,5 при неудачных пробах (f(x[ki]) >f(x[k])) и b = 3 при удачных пробах (f(x[ki]) < f(x[k])). В отличие от других методов нулевого порядка алгоритм Розенброка ориентирован на отыскание оптимальной точки в каждом направлении, а не просто на фиксированный сдвиг по всем направлениям. Величина шага в процессе поиска непрерывно изменяется в зависимости от рельефа поверхности уровня. Сочетание вращения координат с регулированием шага делает метод Розенброка эффективным при решении сложных задач оптимизации.

Дата добавления: 2018-06-01; просмотров: 1485; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 Следующая ⇒

Мы поможем в написании ваших работ!