Пример 3.5. Минимизация на основе свойства параллельного подпространства.
Опять рассмотрим квадратичную функцию q(x) = 4x 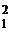 + 3x
+ 3x 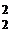 - 4x
- 4x  x
x 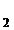 + x
+ x 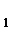 . Пусть заданы две точки х(1) = [0, 0]
. Пусть заданы две точки х(1) = [0, 0]  , х(2) = [1,0]
, х(2) = [1,0]  и направление d = [l, 1]T. Первый поиск проводится вдоль прямой
и направление d = [l, 1]T. Первый поиск проводится вдоль прямой
x = [0, 0]  + λ [1, 1]
+ λ [1, 1] 
и приводит к точке y(1) = [- 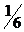 ,-
,- 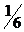 ]
]  (λ*= -
(λ*= - 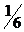 ). Второй поиск проводится вдоль прямой
). Второй поиск проводится вдоль прямой
x = [1, 0]  + λ [1, 1]
+ λ [1, 1] 
и позволяет получить точку y(2) = [ 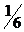 ,–
,– 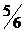 ]
]  (λ*= –
(λ*= – 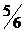 ). Согласно свойству параллельного подпространства, направление
). Согласно свойству параллельного подпространства, направление
y(2) – y(1) = [ 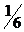 ,–
,– 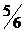 ]
]  – [–
– [– 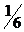 ,–
,– 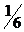 ]
]  = [
= [ 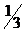 ,–
,– 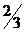 ]
] 
сопряжено с d = [l, 1]T
[l, 1]C[ 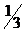 ,–
,– 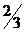 ]
]  .
.
Выше отмечалось, что в случае двух переменных оптимум q(x) можно найти путем проведения поиска вдоль прямой, заданной направлением (y(2) – y(1) ). Этот факт нетрудно проверить, поскольку минимум q(x) вдоль прямой
x = [– 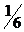 ,–
,– 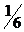 ]
]  + λ [
+ λ [ 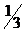 ,–
,– 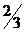 ]
] 
достигается в точке х* = [–  ,–
,–  ]T(λ* = –
]T(λ* = – 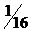 ), которая совпадает с полученным ранее решением.
), которая совпадает с полученным ранее решением.
В рассмотренных выше построениях для того, чтобы определить сопряженное направление, требовалось задать две точки и некоторое направление. Это не слишком удобно при проведении расчетов, поэтому предпочтительнее строить систему сопряженных направлений, исходя из одной начальной точки, что легко осуществить при помощи единичных координатных векторов е(1), е(2), е(3),..., е(N). (Здесь рассматривается процедура построения сопряженных направлений в случае двух переменных, которая допускает очевидное обобщение для N-мерного пространства.) Пусть е(1) = [l, 0]  и е(2) = [0, 1]
и е(2) = [0, 1]  . При заданной начальной точке х(0) вычислим значение λ(0), которому соответствует минимум f (х(0) + λ(0) е(1)).
. При заданной начальной точке х(0) вычислим значение λ(0), которому соответствует минимум f (х(0) + λ(0) е(1)).
|
|
|
Положим
x(1) = х(0) + λ(0) е(1).
и вычислим значение λ(1), которому соответствует минимум f (х(1) + λ(1) е(2)). Положим
x(2) = х(1) + λ(1) е(2).
Далее вычислим значение λ(2), минимизирующее f (х(2) + λ(2) е(1)), и положим
x(3) = х(2) + λ(2) е(1).
При этом направления (х(3) – х(1)) и е(1) оказываются сопряженными. Для того чтобы убедиться в этом, рассмотрим рис. 3.11. Заметим, что точка х(1) найдена в результате поиска из точки х(0) в направление е(1), а точка х(3) получена при поиске из точки х(2) в направлении е(1). Следовательно, направление е(1) и (х(3) – х(1)) являются сопряжёнными согласно свойству параллельного подпространства. Далее если на следующей итерации провести поиск в направлении (x(3) – x(1)), то процедура поиска будет охватывать два сопряженных направления, и поскольку f(x) предполагается квадратичной функцией двух переменных, в результате будет найдено решение х*.
Проведенное на основе свойства параллельного подпространства построение рассмотрено для случая, когда число сопряженных направлений равняется двум. Однако это построение естественным образом обобщается на случай задач более высокой размерности
В частности, нетрудно показать, что если точка y(1) найдена в результате поиска из точки х(1) вдоль каждого из М (<N) сопряженных направлений, а точка y(2) получена в результате поиска из точки х(2) вдоль каждого из тех же М сопряженных направлений s(1), s(2), s(3),..., s(M) то вектор (y(2) – y(1)) задает направление, сопряженное со всеми выбранными М направлениями. Это утверждение известно как обобщенное свойство параллельного подпространства. Используя указанное свойство, можно обобщить метод построения сопряженных направлений, последовательные шаги реализации которого отражены на рис. 3.11 на случай пространства управляемых переменных более высокой размерности. Рис. 3.12 иллюстрирует построение сопряженных направлений в трехмерном пространстве.
|
|
|
Как показано на рис. 3.12, сначала поиск осуществляется вдоль трех координатных направлений е(1), е(2) и е(3) затем эти направления последовательно заменяются вновь построенными сопряженными направлениями. Серия одномерных поисков из точки x(0) проводится в направлении е(3), затем е(1), е(2) и снова е(3); в результате построены сопряженные направления е(3) и (x(4) – x(1)). Направление е(1) заменяется новым направлением поиска, которое на рис. 3.12 обозначено цифрой 4. Следующая серия поисков проводится в направлении 4, затем е(2), е(3) и снова 4. Согласно обобщенному свойству параллельного подпространства, новое направление (x(8) – x(5)), обозначенное на рисунке цифрой 5, сопряжено не только с 4, но и с е(3). Следовательно, направления е(3), (x(4) – x(1)) и (x(8) – x(5)) образуют систему взаимно сопряженных направлений.
|
|
|

Рис. 3.11. Построение сопряженных направлений из одной точки.
Поэтому если провести дополнительный поиск из точки x(5) в направлении (x(8) – x(5)) (т. е. в направлении 5 на рисунке), то будет найдена точка x(9), в которой должен достигаться оптимум квадратичной функции трех переменных f(x), поскольку поиск последовательно осуществляется в трех взаимно сопряженных направлениях. Таким образом, в трехмерном случае для нахождения точного (если, разумеется, оперировать недесятичными дробями) оптимума квадратичной функции требуется провести девять поисков вдоль прямой с использованием только значений функции. Алгоритм легко обобщается и в случае N-мерного пространства требует проведения последовательности N 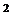 одномерных поисков, которая приводит к получению точки оптимума квадратичной функции. Ниже представлены шаги обобщенного алгоритма.
одномерных поисков, которая приводит к получению точки оптимума квадратичной функции. Ниже представлены шаги обобщенного алгоритма.
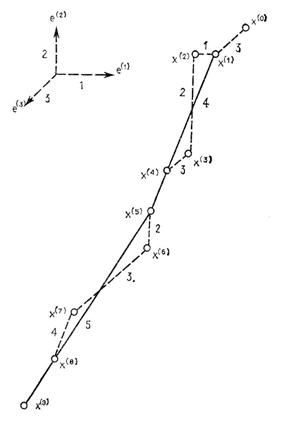
Рис. 3.12. Построение сопряженных направлений в трехмерном пространстве.
|
|
|
Дата добавления: 2018-06-01; просмотров: 377; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
