Пример 3.4. Преобразование к виду суммы квадратов
Рассмотрим функцию
f(x) = 4x 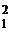 + 3x
+ 3x 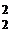 – 4x
– 4x  x
x 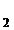 + x
+ x 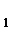
и преобразование
x  = z
= z 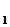 + ½ z
+ ½ z 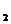 , x
, x 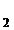 = z
= z 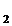 ,
,
или
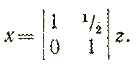
Преобразованная квадратичная функция принимает следующий вид:
f(z)= 4z 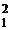 + 2z
+ 2z 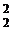 + z
+ z 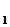 + ½ z
+ ½ z  .
.
Заметим, что это преобразование не является единственным, поскольку система векторов t  не удовлетворяет условию ортонормированности. В частности, нетрудно проверить, что преобразование
не удовлетворяет условию ортонормированности. В частности, нетрудно проверить, что преобразование
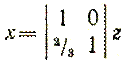
также приводит матрицу квадратичной формы к диагональному, виду. Задавая начальную точку x  = [0, 0]
= [0, 0] 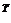 и два столбца матрицы преобразования
и два столбца матрицы преобразования
t 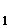 = [1, 0]
= [1, 0] 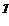 , t
, t 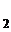 = [½, 1]
= [½, 1] 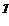 ,
,
можно найти точку оптимума [–  ,–
,–  ]T в результате проведения двух последовательных поисков в направлениях t
]T в результате проведения двух последовательных поисков в направлениях t 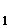 и t
и t 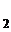 Поиск в направлении t
Поиск в направлении t 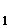 по формуле
по формуле
x 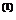 = x
= x 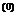 + λt
+ λt 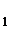
позволяет получить значение λ = –  и точку х(1) =[–
и точку х(1) =[–  , 0]
, 0]  . Далее из точки х(1) проводится поиск в направлении t2. Получаем значение λ = –
. Далее из точки х(1) проводится поиск в направлении t2. Получаем значение λ = –  и решение х(2) = [–
и решение х(2) = [–  ,–
,–  ]T.
]T.
Из рассмотренного примера и предыдущего изложения следует, что если система векторов t  , j = 1,...,N, или система сопряженных направлений, построена, то точку оптимума квадратичной функции можно найти в результате реализации в точности N одномерных поисков, которые проводятся вдоль каждого из N направлений t
, j = 1,...,N, или система сопряженных направлений, построена, то точку оптимума квадратичной функции можно найти в результате реализации в точности N одномерных поисков, которые проводятся вдоль каждого из N направлений t  , j = 1,...,N. Таким образом, нерешенными остаются лишь вопросы, связанные с построением системы векторов t
, j = 1,...,N. Таким образом, нерешенными остаются лишь вопросы, связанные с построением системы векторов t  . Если матрица С известна, то матрицу преобразования Т можно найти с помощью метода Гаусса — Жордана (как это выполнено в приложении А). Метод Гаусса — Жордана позволяет представить матрицу С в виде произведения
. Если матрица С известна, то матрицу преобразования Т можно найти с помощью метода Гаусса — Жордана (как это выполнено в приложении А). Метод Гаусса — Жордана позволяет представить матрицу С в виде произведения
|
|
|
C = PTDP, откуда (3.30)
(P 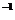 )
) 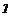 C(P
C(P 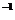 ) = D и T = P
) = D и T = P 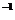 (3.31)
(3.31)
Однако матрица С (или ее оценка) в данном случае неизвестна, поскольку речь идет о построении метода решения задач безусловной оптимизации с целевой функцией f(x), при реализации которого используются только значения функции и не используются значения первых и тем более вторых производных. Тем не менее и в этом случае можно определить систему сопряженных направлений на основе следующего элементарного свойства квадратичных функций.
Свойство параллельного подпространства
Пусть заданы квадратичная функция q(x), две произвольные несовпадающие точки x(1) и х(2),а также направление d. Если точка y(1) минимизирует q(x(1)+λd), a точка y(2) минимизирует q(x(1)+ λd), то направление (y(2) - y(1)) сопряжено с d.
Рис. 3.10 иллюстрирует сформулированное свойство для случая двух переменных. Нетрудно видеть, что поиск, проводимый из точки y(1) или y(2) в направлении (y(2) - y(1)), обеспечивает получение точки минимума. Таким образом, в случае двух переменных реализация трех одномерных поисков позволяет построить систему сопряженных направлений и, кроме того, найти точку оптимума квадратичной функции. Прежде чем продолжать алгоритмические построения, докажем теорему о свойстве параллельного подпространства.
|
|
|

Рис. 3.10. Сопряженные направления на плоскости.
Напомним, что по определению С-сопряженные направления задаются системой вектор-столбцов матрицы Т, которая приводит матрицу С к диагональному виду:
Т 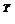 CТ = D (3.32)
CТ = D (3.32)
Поскольку все внедиагональные элементыD равны нулю, отсюда следует, что
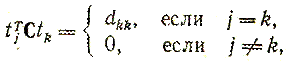 (3.33)
(3.33)
где t  — i-й столбец матрицы Т. Таким образом, мы получили возможность дать более удобное, эквивалентное и, по-видимому, более конструктивное определение сопряженности направлений.
— i-й столбец матрицы Т. Таким образом, мы получили возможность дать более удобное, эквивалентное и, по-видимому, более конструктивное определение сопряженности направлений.
Сопряженные направления
Пусть С — симметрическая матрица порядка N  N; направления s(1), s(2), s(3),..., s
N; направления s(1), s(2), s(3),..., s 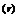 , r ≤ N,называются С-сопряженными, если эти направления линейно независимы и
, r ≤ N,называются С-сопряженными, если эти направления линейно независимы и
s 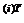 Cs
Cs 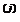 = для всех i ≠ j. (3.34)
= для всех i ≠ j. (3.34)
Опять обратимся к квадратичной функции общего вида
q(x) = a + bTx+(1/t)xTCx.
Точки прямой, исходящей из х(1) в направлении d, задаются формулой
x = x 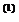 +λd.
+λd.
Минимум q(x) вдоль направления d определяется путем нахождения значения λ*, при котором 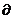 q/
q/ 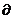 λ=0. Вычислим эту производную по правилу дифференцирования сложной функции:
λ=0. Вычислим эту производную по правилу дифференцирования сложной функции:
|
|
|
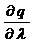 =
= 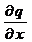
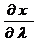 = b
= b 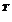 + x
+ x 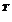 Cd. (3.35)
Cd. (3.35)
По предположению теоремы минимум достигается в точке y(1) следовательно,
[(y(1) ) 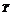 C b
C b 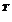 ] d = 0. (3.36)
] d = 0. (3.36)
Аналогично, так как минимум q(x) при движении из точки х(2) в направлении d достигается в точке y(2) имеем
[(y(2) ) 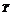 C b
C b 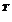 ] d = 0. (3.37)
] d = 0. (3.37)
Вычитая (3.36) из (3.37), получаем
(y(2) - y(1) ) 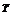 Cd = 0 (3.38)
Cd = 0 (3.38)
В соответствии с данным выше определением направления d и (y(2) - y(1) ) оказываются С-сопряженными, и свойство параллельного подпространства для квадратичных функций доказано.
Дата добавления: 2018-06-01; просмотров: 374; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
