Пример 3.3. Поиск по методу Хука — Дживса
Найти точку минимума функции
f(x) = 8x 
+ 4x 
x 
+ 5x 
,
используя начальную точку х(0)=[ –4, –4]T.
Решение. Для того чтобы применить метод прямого поиска Хука — Дживса, необходимо задать следующие величины:
∆x — векторная величина приращения = [1, 1] 
,
α — коэффициент уменьшения шага = 2,
ε — параметр окончания поиска — 10—4.
Итерации начинаются с исследующего поиска вокруг точки х(0),которой соответствует значение функции f(х(0)) = 272. Фиксируя x2, дадим приращение переменной x :
x = –4
x = –4+1→ f(–3, –4) = 200< f(х(0)) → Успех.
Следовательно, необходимо зафиксировать x = –3 и дать приращение переменной х2:
x = –3,
x = –4+1→ f(–3, –3) = 153< 200 → Успех.
Таким образом, в результате исследующего поиска найдена точка
x =[–3, –3] 
, f(x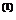 
) = 153
Поскольку исследующий попек был удачным, переходим к поиску по образцу:
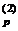x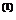 
= x +( x 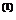– х(0)) = [–2, –2] ,
f(x 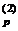) = 68
Далее проводится исследующий поиск вокруг точки x 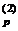который оказывается удачным при использовании положительных приращений переменных x и x . В результате получаем точку
x 
= [–1, –1] 
, f(x ) = 17.
Поскольку f(x(2)) < f(x(1)), поиск по образцу следует считать успешным, и х(2) становится новой базовой точкой при следующем проведении поиска по образцу. Итерации продолжаются, пока уменьшение величины шага не укажет на окончание поиска в окрестности точки минимума х* = [0, 0]T. Последовательные шаги реализации метода показаны на рис. 3.7.
|
|
|
Из примера 3.3 следует, что метод Хука — Дживса характеризуется несложной стратегией поиска, относительной простотой вычислений и невысоким уровнем требований к объему памяти ЭВМ, который оказывается даже ниже, чем в случае использования метода поиска по симплексу. Благодаря этому алгоритм Хука — Дживса находит широкое применение во всех областях инженерной практики; особенно эффективны его варианты с использованием штрафных функций, которые рассматриваются в гл. 6. Однако необходимо отметить, что основанный на циклическом движении по координатам алгоритм в ряде случаев может заканчивать работу преждевременно, а при наличии значительных нелинейных эффектов вырождается в последовательность исследующих поисков без перехода к ускоряющемуся поиску по образцу.
Известен целый ряд подходов к усовершенствованию метода Хука — Дживса. В частности, Бендлер и Мак-Дональд [11] модифицировали процедуру Хука — Дживса путем введения дополнительных правил увеличения и уменьшения приращений переменных, а также правила уменьшения шага по образцу, которое применяется в тех случаях, когда обычный шаг оказывается неудачным. Эксперименты, проведенные авторами данной книги, позволили доработать другую фазу реализации алгоритма, которую иногда называют использованием образца. Если движение по образцу приводит к успеху, имеются определенные основания для того, чтобы полностью использовать возможности поиска вдоль прямой, определяемой образцом, или по крайней мере увеличить длину шага по образцу. Такие действия часто позволяют существенно ускорить сходимость метода. Эмери и О'Хаган [12] изменили фазу исследующего поиска путем введения системы ортогональных направлений поиска, ориентация которой случайным образом меняется на каждой итерации. Розенброк [13] разработал метод, в котором, как и в методе Хука — Дживса, новое направление поиска определяется с учетом информации, полученной на предыдущих итерациях. Однако (в отличие от метода Хука—Дживса) подход, предложенный Розенброком, основан на непрерывном изменении множества векторов, используемых при исследующем поиске, с помощью процедуры ортогонализации. Другой метод, изложенный в работе Свенна [14] и иногда называемый методом поиска Дэвиса, Свенна и Кемпи, опирается на стратегию поиска, подобную стратегии Розенброка. При его реализации поиск ведется не с помощью фиксированных шагов по каждому из выбранных направлений, а вдоль каждой прямой, заданной одним из направлений 1). Каждый из перечисленных методов прямого поиска обладает рядом преимуществ перед остальными при решении задач определенного типа.
|
|
|
|
|
|
f(x) = 8x + 4x x + 5x
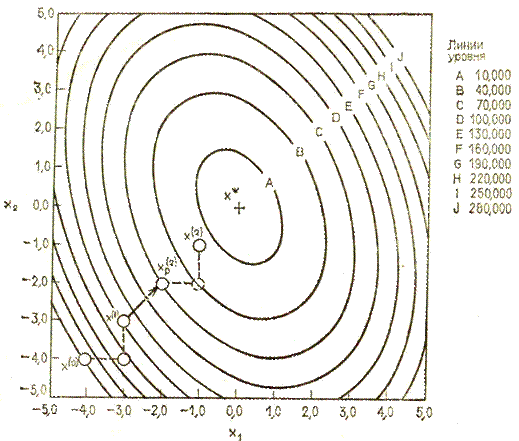
3.7. Итерация поиска по методу Хука—Дживса в примере 3.3.
1) Методы Розенброка и Дэвиса, Свенна, Кемпи более подробно изложены в книге Химмельблау [69], переведенной на русский язык,— Прим. Перев
Вместе с тем вопрос о том, являются ли дополнительные усложнения метода Хука — Дживса оправданными, по-видимому, остается открытым. Если же существует возможность реализовать более сложный алгоритм, то предпочтение следует отдать методу Пауэлла, превосходство которого над рассмотренными выше эвристическими методами несомненно.
Дата добавления: 2018-06-01; просмотров: 1859; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!