Методы сопряженных градиентов

⇐ ПредыдущаяСтр 10 из 15Следующая ⇒

В предыдущих подразделах рассматривались методы Коши и Ньютона. Отмечалось, что метод Коши эффективен при поиске на значительных расстояниях от точки минимума х* и плохо «работает» в окрестности этой точки, тогда как метод Ньютона не отличается высокой надежностью при поиске х* из удаленной точки, однако оказывается весьма эффективным в тех случаях, когда x⁽^k⁾находится вблизи точки минимума. В этом и последующих подразделах рассматриваются методы, которые обладают положительными свойствами методов Коши и Ньютона и основаны на вычислении значений только первых производных. Таким образом, эти методы, с одной стороны, отличаются высокой надежностью при поиске х* из удаленной точки х* и, с другой стороны, быстро сходятся в окрестности точки минимума.

Методы, позволяющие получать решения задач с квадратичными целевыми функциями приблизительно за N шагов при условии использования недесятичных дробей, будем называть квадратично сходящимися. Среди таких методов можно выделить класс алгоритмов, в основе которых лежит построение сопряженных направлений. Выше было сформулировано условие сопряженности для системы направлений s⁽^k⁾, k = 1, 2, 3,…, r ≤ N, и симметрической матрицы С порядка N N. Была также установлена связь между построением указанных направлений и преобразованием произвольной квадратичной функции к виду суммы полных

¹⁾Задачи такого типа возникают, например, в регрессионном анализе — Прим. перев.

квадратов; сделан вывод о том, что последовательный поиск вдоль каждого из N направлений, обладающих свойством С-сопряженности, позволяет найти точку минимума квадратичной функции N переменных. Рассмотрена процедура определения системы сопряженных направлений с использованием только значений целевой функции. Ниже для получения сопряженных направлений применяются квадратичная аппроксимация f(x) и значения компонент градиента. Кроме того, потребуем, чтобы рассматриваемые методы обеспечивали убывание целевой функции при переходе от итерации к итерации.

Пусть в пространстве управляемых переменных заданы две произвольные несовпадающие точки x⁽⁰⁾ и x⁽¹⁾. Градиент квадратичной функции равен

f(x) = q(x) = Cx + b = g(x) (3.60)

Обозначение g(x) введено здесь для удобства записи формулы. Таким образом,

g(x⁽⁰⁾) = Cx⁽⁰⁾ + b,

g(x⁽¹⁾) = Cx⁽¹⁾ + b.

Запишем изменение градиента при переходе от точки х⁽⁰⁾ к точке х⁽¹⁾:

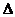g(x) = g(x⁽¹⁾) – g(x⁽⁰⁾) = C(x⁽¹⁾ - x⁽⁰⁾), (3.61)

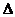g(x) = C 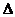x

Равенство (3.61) выражает свойство квадратичных функций, которое будет использовано ниже.

В 1952 г. Эстенс и Штифель [28] предложили эффективный итерационный алгоритм для решения систем линейных уравнений, который по существу представлял собой метод сопряженных градиентов. Они рассматривали левые части линейных уравнений как компоненты градиента квадратичной функции и решали задачу минимизации этой функции. Позже Флетчер и Ривс [29] обосновали квадратичную сходимость метода и обобщили его для случая неквадратичных функций. Фрид и Метцлер [30] продемонстрировали (допустив, однако, некоторые неточности) возможности использования метода для решения линейных систем с разреженной матрицей коэффициентов. (Определение разреженной матрицы см. в приложении А.) Они подчеркнули простоту реализации метода по сравнению с другими, более общими алгоритмами, что является особенно важной характеристикой с позиций нашего изложения.

Рассмотрение метода будем проводить в предположении, что "целевая функция является квадратичной:

f(x) = q(x) = a + b^T x + ½ x^T Cx,

аитерации проводятся по формуле (3.42), т.е.

x 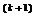= x + α s(x ).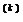

Направления поиска на каждой итерации определяются с помощью следующих формул:

s⁽^k⁾ = – g⁽^k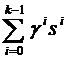⁾ + (3.62)

s⁽⁰⁾ = –g⁽⁰⁾, (3.63)

где g⁽^k⁾ = f(x 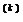). Так как после определения системы направлений проводится последовательный поиск вдоль каждого из направлений, полезно напомнить, что в качестве критерия окончания одномерного поиска обычно используется условие

f (x 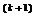)^Ts⁽^k⁾ = 0 (3.64)

Значения 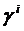, i = 1, 2, 3,...,k - 1,выбираются таким образом, чтобы направление s⁽^k⁾ было С-сопряжено со всеми построенными ранее направлениями поиска. Рассмотрим первое направление

s⁽¹⁾ = –g⁽¹⁾ + γ⁽⁰⁾s⁽⁰⁾ = –g⁽¹⁾ –γ⁽⁰⁾g⁽⁰⁾

и наложим условие его сопряженности с s⁽⁰⁾

s^(1)T Cs⁽⁰⁾ = 0,

откуда [g⁽¹⁾ + γ⁽⁰⁾g⁽⁰⁾]^TCs⁽⁰⁾ = 0.

На начальной итерации

s⁽⁰⁾ = ;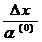

следовательно,

[g⁽¹⁾ + γ⁽⁰⁾g⁽⁰⁾]^TC[ 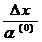] = 0

Используя свойство квадратичных функций (3.61), получаем

[g⁽¹⁾ + γ⁽⁰⁾g⁽⁰⁾]^T 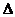g = 0, (3.65)

Откуда

γ⁽⁰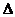⁾ = – ( g^T g⁽¹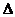⁾)/( g^T g⁽⁰⁾). (3.66)

Из уравнения (3.65) следует, что

g^(1)Tg⁽¹⁾ + γ⁽⁰⁾g^(0)Tg⁽¹⁾ – g^{(1) T}g⁽⁰⁾ – γ⁽⁰⁾g^(0)Tg⁽⁰⁾ = 0.

При соответствующем выборе α⁽⁰⁾ и с учетом формулы (3.64) имеем

g^{(1) T}g⁽⁰⁾ = 0.

Таким образом,

γ⁽⁰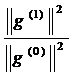⁾ = . (3.67)

Далее определим следующее направление поиска

s⁽²⁾ = –g⁽²⁾ + γ⁽⁰⁾s⁽⁰⁾ + γ⁽¹⁾s⁽¹⁾.

и выберем γ⁽⁰⁾ γ⁽¹⁾ таким образом, чтобы выполнялись условия

s⁽²⁾^TCs⁽⁰⁾ = 0 и s⁽²⁾Cs⁽¹⁾ = 0,

т. е. условия С-сопряженности направления s⁽²⁾ с направлениями s⁽⁰⁾ и s⁽¹⁾. С помощью формул (3.61) и (3.64) можно показать (это предоставляется читателю в качестве упражнения), что здесь γ⁽⁰⁾ = 0, а в общем случае γ⁽ⁱ⁾ = 0, i = 0, 1, 2,...,k—2, при любом значении k. Отсюда следует, что общая формула для направлений поиска может быть записана в виде, предложенном Флетчером и Ривсом:

s^(k) = –g^(k) + 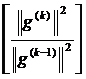s 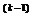(3.68)

Если f(x) — квадратичная функция, для нахождения точки минимума требуется определить N—1 таких направлений и провести N поисков вдоль прямой (при отсутствии ошибок округления). Если же функция f(х) не является квадратичной, количество направлений и соответствующих поисков возрастает.

Некоторые исследователи на основе опыта проведения вычислительных экспериментов предлагают после реализации каждой серии из N или N + 1 шагов возвращаться к начальной итерации алгоритма, положив s(x) = -g(x). Это предложение остается предметом для изучения, поскольку при минимизации функций общего вида в ряде случаев влечет за собой замедление сходимости. С другой стороны, циклические переходы к начальной итерации повышают надежность алгоритма, так как вероятность построения линейно зависимых направлений уменьшается. Если полученное направление оказывается линейной комбинацией одного или нескольких полученных ранее направлений, то метод может не привести к получению решения, поскольку поиск в соответствующем подпространстве R^N уже проводился. Однако следует отметить, что на практике такие ситуации встречаются достаточно редко. Метод оказывается весьма эффективным при решении практических задач, характеризуется простотой однопараметрической вычислительной схемы и небольшим объемом памяти ЭВМ, необходимым для проведения поиска. Относительно невысокий уровень требований к объему памяти ЭВМ делает метод Флетчера — Ривса (ФР) и его модификации особенно полезным при решении задач большой размерности.

Дата добавления: 2018-06-01; просмотров: 629; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!