Обобщенный градиентный алгоритм
Сходство методов сопряженных градиентов и квазиньютоновских методов дает основание для разработки обобщенного алгоритма, в основе которого лежит использование ряда рассмотренных выше методов. Таким алгоритмом является обобщенный градиентный алгоритм.
Обобщенный градиентный алгоритм
Шаг 1.Задать М — максимальное (допустимое) количество итераций; N — количество переменных; х(0) — начальное приближение к х*; ε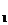 
— параметр сходимости алгоритма; ε 
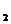— параметр сходимости для поиска вдоль прямой.
Шаг 2.Положить k = 0.
Шаг 3.Вычислить компоненты 
f (x 
).
Шаг 4.Выполняется ли неравенство || f (x )|| ≤ ε ?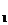
Да: печать «сходимость: градиент»; перейти к шагу 13.
Нет:. перейти к следующему шагу.
Шаг 5.Выполняется ли равенство k > М?
Да: печать «окончание поиска: k = M»;перейти к шагу 13.
Нет: перейти к следующему шагу.
Шаг 6.Вычислить s(x ).
Шаг 7.Выполняется ли неравенство f (x ) 
s(x ) < 0?
Да: перейти к шагу 9.
Нет: положить s(x ) = – f (x ) .
1)В отечественной литературе используется также термин «условный градиент».— Прим. перев.
Печать «возврат: неудачное направление». Перейти к шагу 9.
Шаг 8.Найти такое значение α 
, при котором f (x + α + s(x )) → min (используя параметр ε ).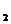
Шаг 9.Положить x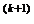 
= x + α s(x ).
Шаг 10.Выполняется ли неравенство f (x 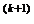) < f (x )?
Да: перейти к шагу 11.
Нет: печать «окончание поиска: нет уменьшения функции», перейти к шагу 13.
Шаг 11.Выполняется ли неравенство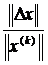 
≤ ε ?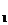
|
|
|
Да: печать «окончание поиска: нет продвижения к решению»; перейти к шагу 13.
Нет: перейти к шагу 12.
Шаг 12.Положить k = k +1. Перейти к шагу 3.
Шаг 13.Останов.
В описанном алгоритме можно использовать различные методы путем определения соответствующих направлений поиска на шаге 6. Вычисления, требуемые для реализации того или иного метода, проводятся по приведенным выше формулам. Отдельные шаги алгоритма (в частности, шаг 7) не соответствуют случаю, когда применяется метод Коши, однако алгоритм этого метода подробно рассматривался ранее. Можно было бы ввести в алгоритм процедуру возврата к начальной итерации для метода Флетчера — Ривса, но вместе с тем тесты, включенные в алгоритм, обеспечивают обнаружение любых трудностей, ассоциированных с необходимостью возврата при расчетах по методу сопряженных градиентов.
На шаге 7 можно реализовать дополнительную проверку в соответствии с предложениями Била и Пауэлла относительно возврата к началу алгоритма. Кроме того, повышению эффективности алгоритма способствует включение в шаг 8 дополнительных процедур, предложенных Дэвидоном, Пауэллом и Шэнно. Отметим, что в процессе одномерного поиска следует по возможности избегать точных вычислений; проведенные авторами данной книги эксперименты показывают, что на выполнение операций поиска вдоль прямой тратится весьма значительная часть общего времени счета по программе.
Дата добавления: 2018-06-01; просмотров: 557; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!