Пример 3.9. Метод Флетчера — Ривса
Найти точку минимума функции
f(x) = 4x  + 3x
+ 3x  – 4x
– 4x  x
x  + x
+ x 
если x  = [0, 0]T.
= [0, 0]T.
Решение.
Шаг 1.  f(x) = [8x
f(x) = [8x  -4x
-4x 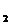 +1, 6x
+1, 6x 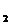 -4x
-4x  ]T,
]T,
s(0) = –  f(x(0)) = – [1, 0]T.
f(x(0)) = – [1, 0]T.
Шаг 2.Поиск вдоль прямой:
x  = x
= x  –α
–α 
 f(x(0)) → α
f(x(0)) → α  = ⅛,
= ⅛,
x  = [0, 0]T – ⅛ [1, 0]T = [–⅛, 0]T
= [0, 0]T – ⅛ [1, 0]T = [–⅛, 0]T
Шаг 3.k = 1.
s(1) = – [0, ½]T – [¼, 1] [1, 0]T = [–¼, ½]T.
Шаг 4.Поиск вдоль прямой:
x  = x
= x  + α
+ α  s(1) → α
s(1) → α  = ¼,
= ¼,
x  = [–⅛, 0]T – ¼ [¼, ½]T = [–
= [–⅛, 0]T – ¼ [¼, ½]T = [–  ,
,  ]T,
]T,
 f(x(2)) = [0, 0]T.
f(x(2)) = [0, 0]T.
Таким образом, x  = х*. Решение получено в результате проведения двух одномерных поисков, поскольку целевая функция квадратичная, а ошибки округления отсутствуют.
= х*. Решение получено в результате проведения двух одномерных поисков, поскольку целевая функция квадратичная, а ошибки округления отсутствуют.
Миль и Кентрелл [31] обобщили подход Флетчера и Ривса, предложив формулу
x  = x
= x  + α
+ α  {–
{–  f(x(k)) + γ
f(x(k)) + γ  s(x
s(x  )} (3.69)
)} (3.69)
где α  и γ
и γ  — параметры, значения которых определяются на каждой итерации. Этот метод, известный как градиентный метод с памятью,очень эффективен по числу необходимых для решения задачи итераций, но требует большего количества вычислений значений функции и компонент градиента, чем метод Флетчера — Ривса. Поэтому алгоритм Миля и Кентрелла оказывается полезным лишь в тех случаях, когда оценивание значений целевой функции и компонент градиента не связано с какими-либо трудностями.
— параметры, значения которых определяются на каждой итерации. Этот метод, известный как градиентный метод с памятью,очень эффективен по числу необходимых для решения задачи итераций, но требует большего количества вычислений значений функции и компонент градиента, чем метод Флетчера — Ривса. Поэтому алгоритм Миля и Кентрелла оказывается полезным лишь в тех случаях, когда оценивание значений целевой функции и компонент градиента не связано с какими-либо трудностями.
Напомним, что рассмотрение метода Флетчера — Ривса проводилось в предположении квадратичности целевой функции и отсутствия ошибок округления в процессе поиска вдоль прямой. Однако при реализации ряда методов сопряженные направления определяются без учета одного из указанных предположений (или даже обоих предположений). Среди таких методов наибольшего внимания, по-видимому, заслуживает метод, разработанный Ползком и Рибьером [32] в 1969 г. Метод основан на точной процедуре проведения поиска вдоль прямой и на более общем предположении об аппроксимации целевой функции. При этом
|
|
|
γ  =
=  , (3.70)
, (3.70)
где, как и прежде,
 g(x
g(x  )= g(x
)= g(x  ) – g(x
) – g(x  ). (3.71)
). (3.71)
Если α — параметр, значение которого определяется в результате поиска вдоль прямой, и γ — параметр, значение которого вычисляется по формуле (3.70), то метод сопряженных градиентов Полака — Рибьера реализуется с помощью следующих соотношений:
x  = x
= x  + α
+ α  s(x
s(x  ),
),
s(x  ) = –
) = –  f (x
f (x  ) + γ
) + γ  s(x
s(x  ). (3.72)
). (3.72)
Легко видеть, что единственное различие между методами Полака — Рибьера и Флетчера — Ривса заключается в способах выбора параметра γ.
Известны и другие подобные методы, которые также основаны на проведении точных вычислений при одномерном поиске и на более общей (чем квадратичная) аппроксимации целевой функции (см., например, [33, 34, 35]). Краудер и Вульф [36] в 1972 г., а затем Пауэлл [37] доказали, что методы сопряженных градиентов обладают линейной скоростью сходимости при отсутствии периодического возврата к начальной итерации. Указанные возвраты осуществляются в соответствии со специальной процедурой, которая прерывает процесс построения векторов направлений поиска, а далее вычисления продолжаются по аналогии с построением s(x(0)). Выше отмечалось, что по ряду причин наличие процедуры возврата к начальной итерации повышает устойчивость работы алгоритма, так как позволяет избежать построения линейно зависимых векторов направлений поиска. Пауэлл [38] доказал, что метод Полака — Рибьера также характеризуется линейной скоростью сходимости при отсутствии возвратов к начальной итерации, однако имеет несомненное преимущество перед методом Флетчера — Ривса при решении задач с целевыми функциями общего вида и обладает менее высокой чувствительностью к ошибкам округления при проведении одномерных поисков.
|
|
|
Вопросы разработки эффективных процедур и методов, обеспечивающих возврат к начальной итерации и при этом обладающих малой чувствительностью к ошибкам округления, остаются предметом активных исследований. Бил [39] предложил метод сопряженных градиентов, аналогичный стандартной процедуре Флетчера — Ривса, но вместе с тем не использующий направление вдоль градиента при возвращении к начальной итерации. Он показал, как на основе анализа направления, полученного непосредственно перед возвращением к начальной итерации, можно уменьшить объем необходимых вычислений при решении задач, требующих нескольких возвратов. Пауэлл [38] исследовал стратегию Била, а также другие стратегии возврата к начальной итерации и предложил использовать процедуру возврата либо после проведения каждой серии из N шагов, либо при выполнении неравенства
|
|
|
| g(x  )Tg(x
)Tg(x  ) | ≥ 0.2 ||g(x
) | ≥ 0.2 ||g(x  )||
)||  . (3.73)
. (3.73)
Он продемонстрировал, что стратегию Била, дополненную условием (3.73), можно успешно применять как вместе с формулой Флетчера — Ривса, так и с формулой Полака — Рибьера, и провел ряд вычислительных экспериментов, результаты которых подтверждают превосходство метода Полака — Рибьера (с возвратом). Шэнно [40] исследовал влияние ошибок округления при проведении поисков вдоль прямой и различных стратегий возврата на эффективность методов сопряженных градиентов. Он показал, что стратегия Била (с использованием соответствующей двухпараметрической формулы), дополненная предложенным Пауэллом условием возврата, приводит к существенному уменьшению требуемой точности одномерного поиска и, следовательно, к значительному повышению эффективности полной вычислительной схемы метода сопряженных градиентов. Шэнно также представил численные результаты, которые указывают на преимущество метода Полака — Рибьера с использованием процедур возврата и округления при поисках вдоль прямой. В работе [41] продемонстрирована ведущая роль методов сопряженных градиентов при решении задач нелинейного программирования большой размерности.
|
|
|
Квазиньютоновские методы
Эти методы подобны методам, рассмотренным в подразд. 3.3.5, поскольку также основаны на свойствах квадратичных функций. В соответствии с изложенными выше методами поиск решения осуществляется по системе сопряженных направлений, тогда как квазиньютоновские методы обладают положительными чертами метода Ньютона, однако используют только первые производные. Во всех методах указанного класса построение векторов направлений поиска осуществляется с помощью формулы (3.42), в которой s(x(k))записывается в виде
s(x  ) = –A
) = –A 
 f (x
f (x  ), (3.74)
), (3.74)
где A  — матрица порядка N
— матрица порядка N  N, которая носит название метрики. Методы поиска вдоль направлений, определяемых этой формулой, называются методами переменной метрики, поскольку матрица А изменяется на каждой итерации. Более точно метод переменной метрики представляет собой квазиньютоновский метод, если в соответствии с ним перемещение пробной точки удовлетворяет следующему условию:
N, которая носит название метрики. Методы поиска вдоль направлений, определяемых этой формулой, называются методами переменной метрики, поскольку матрица А изменяется на каждой итерации. Более точно метод переменной метрики представляет собой квазиньютоновский метод, если в соответствии с ним перемещение пробной точки удовлетворяет следующему условию:
 x = C
x = C 
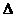 g. (3.75)
g. (3.75)
К сожалению, в специальной литературе не выработаны единые и твердые рекомендации по использованию приведенных выше терминов [42]; мы будем считать их взаимозаменяемыми, поскольку они несут одинаково важную информацию об особенностях разработки и реализации рассматриваемых методов.
Для аппроксимации матрицы, обратной матрице Гессе, воспользуемся следующим рекуррентным соотношением:
A  = A
= A  + A
+ A  (3.76)
(3.76)
где A  — корректирующая матрица. Матрица A
— корректирующая матрица. Матрица A  будет использоваться в формулах (3.74) и (3.42). Задача заключается в том, чтобы построить матрицу A
будет использоваться в формулах (3.74) и (3.42). Задача заключается в том, чтобы построить матрицу A  таким образом, чтобы последовательность А(0), А(1), А(2),...,A(k+1) давала приближение к Н-1 =
таким образом, чтобы последовательность А(0), А(1), А(2),...,A(k+1) давала приближение к Н-1 = 
 f (x*)-1; при этом для получения решения х* требуется один дополнительный поиск вдоль прямой, если f(x) — квадратичная функция. Как неоднократно подчеркивалось выше, имеются определенные основания полагать, что метод, обеспечивающий нахождение оптимумов квадратичных функций, может привести к успеху при решении задач с нелинейными целевыми функциями общего вида.
f (x*)-1; при этом для получения решения х* требуется один дополнительный поиск вдоль прямой, если f(x) — квадратичная функция. Как неоднократно подчеркивалось выше, имеются определенные основания полагать, что метод, обеспечивающий нахождение оптимумов квадратичных функций, может привести к успеху при решении задач с нелинейными целевыми функциями общего вида.
Вернемся к важному свойству квадратичных функций (3.75) и предположим, что матрица С-1 аппроксимируется по формуле
С-1 = βA  , (3.77)
, (3.77)
где р — скалярная величина. Наиболее предпочтительным является приближение, удовлетворяющее (3.75), т. е.
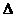 x
x  = A
= A 
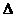 g
g  . (3.78)
. (3.78)
Однако ясно, что построить такую аппроксимацию невозможно, поскольку для того, чтобы найти 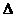 g
g  , необходимо знать матрицу A
, необходимо знать матрицу A  . Здесь используются следующие обозначения:
. Здесь используются следующие обозначения:
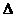 x
x  = x
= x 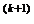 – x
– x  , (3.79)
, (3.79)
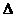 g
g  = g(x
= g(x 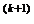 ) – g(x
) – g(x  ). (3.80)
). (3.80)
С другой стороны, можно потребовать, чтобы новое приближение удовлетворяло формуле (3.75):
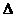 x
x  = βA
= βA 
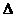 g
g  . (3.81)
. (3.81)
Подставляя выражение (3.76) в (3.81), получаем
A 
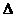 g
g  =
= 
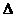 x
x  – A
– A 
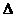 g
g  . (3.82)
. (3.82)
С помощью непосредственной подстановки можно убедиться, что матрица
A  =
= 
 –
– 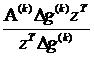 (3.83)
(3.83)
является решением этого уравнения. Здесь у и z— произвольные векторы, т. е. формула (3.83) определяет некоторое семейство решений. Если положить
y = 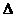 x
x  и z =A
и z =A 
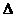 g
g  , (3.84)
, (3.84)
то получим формулу, реализующую известный и широко применяемый метод Дэвидона — Флетчера — Пауэлла (ДФП) [43, 44]:
A  = A
= A  +
+  –
–  . (3.85)
. (3.85)
Можно показать, что эта рекуррентная формула сохраняет свойства симметрии и положительной определенности матриц. Поэтому если А(0) симметрическая положительно определенная матрица,то матрицы А(1), А(2), ... также оказываются симметрическими и положительно определенными при отсутствии ошибок округления; обычно удобно выбирать А(0) = I.
Первая вариация f(x) равна
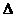 f(x) =
f(x) =  f (x
f (x  )
) 
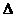 x. (3.86)
x. (3.86)
Используя формулы (3.42) и (3.74), получаем
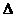 f(x) =
f(x) =  f (x
f (x  )
)  α
α  A
A 
 f (x
f (x  ), (3.87)
), (3.87)
откуда
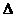 f(x) = – α
f(x) = – α 
 f (x
f (x  )
)  A
A 
 f (x
f (x  ), (3.88)
), (3.88)
и неравенство f (x(k+1)) < f(xk) выполняется при любых значениях α  > 0, если A
> 0, если A  — положительно определенная матрица. Таким образом, алгоритм обеспечивает убывание целевой функции при переходе от итерации к итерации. Метод Дэвидона — Флетчера — Пауэлла в течение ряда лет продолжает оставаться наиболее широко используемым градиентным методом. Он отличается устойчивостью и успешно применяется при решении самых различных задач, возникающих на практике. Основным недостатком методов такого типа является необходимость хранить в памяти ЭВМ матрицу А порядка N
— положительно определенная матрица. Таким образом, алгоритм обеспечивает убывание целевой функции при переходе от итерации к итерации. Метод Дэвидона — Флетчера — Пауэлла в течение ряда лет продолжает оставаться наиболее широко используемым градиентным методом. Он отличается устойчивостью и успешно применяется при решении самых различных задач, возникающих на практике. Основным недостатком методов такого типа является необходимость хранить в памяти ЭВМ матрицу А порядка N  N.
N.
Дата добавления: 2018-06-01; просмотров: 1896; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
