Метод сопряженных направлений Пауэлла
Наиболее эффективным из алгоритмов прямого поиска является метод, разработанный Пауэллом [15], в особенности его модифицированные варианты, предложенные Зангвиллом [16] и Брентой [17]. При работе этого алгоритма информация, полученная на предыдущих итерациях, используется для построения векторов направлений поиска, а также для устранения зацикливания последовательности координатных поисков. Метод ориентирован на решение задач с квадратичными целевыми функциями и основывается на фундаментальных теоретических результатах.
Задачи с квадратичными целевыми функциями занимают важное место в теории оптимизации по двум причинам.
1. Квадратичная функция представляет простейший тип нелинейных функций, для которых может быть сформулирована задача безусловной оптимизации (линейные функции не обладают внутренними оптимумами). Следовательно, если с помощью того или иного метода успешно решаются задачи оптимизации с целевыми функциями общего вида, то такой метод должен оказаться эффективным при решении задач с квадратичными функциями.
2. В окрестности точки оптимума любую нелинейную функцию можно аппроксимировать квадратичной функцией (поскольку линейный член разложения Тейлора обращается в нуль). Следовательно, работа алгоритма при решении задач с квадратичными функциями позволяет получить определенное представление о сходимости алгоритма в случае, когда минимизируется функция общего вида.
|
|
|
Основная идея алгоритма заключается в том, что если квадратичная функция N переменных приведена к виду суммы полных квадратов, то ее оптимум может быть найден в результате реализации N одномерных поисков по преобразованным координатным направлениям.
Процедура преобразования квадратичной функции
q(x) = a + b  x + ½ x
x + ½ x  Cx (3.25)
Cx (3.25)
к виду суммы полных .квадратов эквивалентна нахождению такой матрицы преобразования Т, которая приводит матрицу квадратичной формы к диагональному виду. Таким образом, заданная квадратичная форма
Q(x) = x 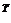 Cx (3.26)
Cx (3.26)
путем преобразования
x = Tz (3.27)
приводится к виду
Q(x) = z 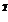 T
T 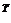 CTz = z
CTz = z 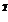 Dz (3.28)
Dz (3.28)
где D — диагональная матрица, т. е. элементы D отличны от нуля только при i = j
f(x) = 4x 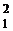 + 3x
+ 3x 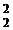 - 4x
- 4x 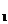 x
x  + x
+ x 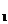
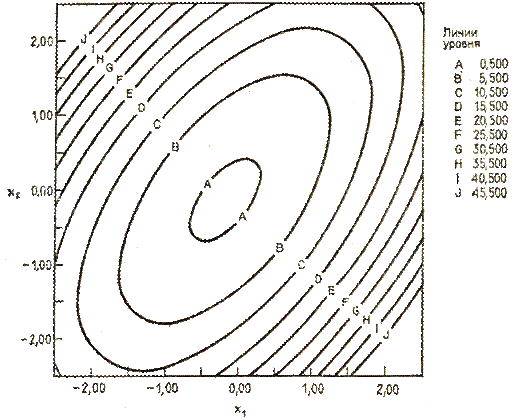
Рис. 3.8. Линии уровня квадратичной функции с перекрёстными членами.
Пусть t 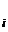 — j-й столбец матрицы Т. Тогда преобразование (3.27) позволяет записать каждый вектор х в виде линейной комбинации вектор-столбцов t
— j-й столбец матрицы Т. Тогда преобразование (3.27) позволяет записать каждый вектор х в виде линейной комбинации вектор-столбцов t 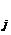 .
.
|
|
|
x = Tz = t  z
z  + t
+ t 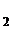 z
z 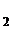 +…+ t
+…+ t 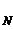 z
z 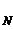 . (3.29)
. (3.29)
Другими словами, вместо координат вектора х в стандартной координатной системе, определяемой множеством векторов e(i), используются координаты вектора в новой координатной системе, заданной векторами t  . Кроме того, система векторов t
. Кроме того, система векторов t  соответствует главным осям рассматриваемой квадратичной формы, поскольку матрица квадратичной формы приводится к диагональному виду. Такая ситуация возникает, если квадратичную функцию с перекрестными членами, линии уровня которой изображены на рис. 3.8, записать в новой координатной системе, оси которой совпадают с большой и малой осями квадратичной функции (см. рис. 3.9).
соответствует главным осям рассматриваемой квадратичной формы, поскольку матрица квадратичной формы приводится к диагональному виду. Такая ситуация возникает, если квадратичную функцию с перекрестными членами, линии уровня которой изображены на рис. 3.8, записать в новой координатной системе, оси которой совпадают с большой и малой осями квадратичной функции (см. рис. 3.9).
Итак, с помощью преобразования переменных квадратичной функции строится новая система координат, совпадающих с главными осями квадратичной функции. Следовательно, одномерный поиск точки оптимума в пространстве преобразованных переменных z эквивалентен поиску вдоль каждой из главных осей квадратичной функции. Так как направления главных осей определяются векторами t  одномерный поиск проводится в направлениях, заданных этими векторами. Проиллюстрируем вышеизложенное примером.
одномерный поиск проводится в направлениях, заданных этими векторами. Проиллюстрируем вышеизложенное примером.
f(x) = 4x 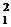 + 2x
+ 2x 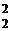 + x
+ x  +
+ 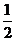 x
x 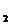
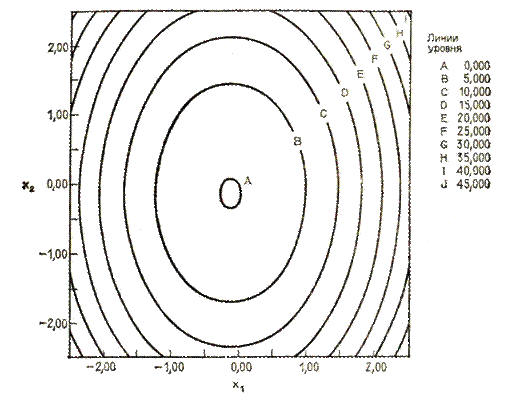
Рис. 3.9. Линии уровня квадратичной функции без перекрёстных членов
|
|
|
Дата добавления: 2018-06-01; просмотров: 838; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
