Приложения определённого интеграла
К вычислению площадей плоских фигур
Рассмотрим частные случаи вычисления площадей плоских фигур с помощью определённого интеграла.
I. Криволинейная трапеция - фигура, ограниченная снизу отрезком 
оси 
, сверху графиком непрерывной функции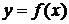 
, принимающей неотрицательные значения на отрезке , а с боков отрезками прямых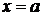 
, 
.
Рис. 5
Площадь криволинейной трапеции вычисляется по формуле 
.
Пример. Вычислим площадь фигуры, ограниченной линиями 
, 
, 
, 
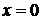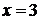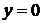. Графиком функции является парабола с вершиной в точке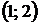 
, ветви которой направлены вверх.
Рис. 6
.
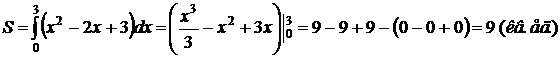II. Отражённая криволинейная трапеция.
Рис. 7
Площадь отражённой криволинейной трапеции вычисляется по формуле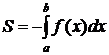 
Пример. Вычислим площадь фигуры, ограниченной графиком функции 
и отрезком 
оси .
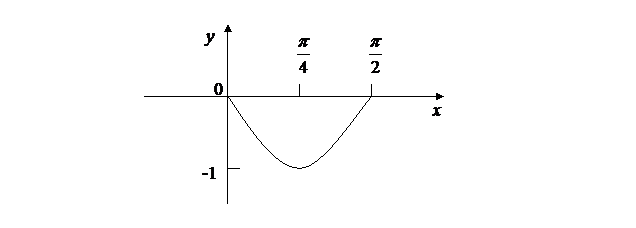
Рис. 8
III. Фигура, состоящая из двух криволинейных трапеций.
Рис. 9
Площадь фигуры, состоящей из двух криволинейных трапеций, вычисляется по формуле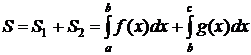 
.
Пример. Вычислим площадь фигуры, ограниченной линиями 
, 
, 
, .
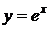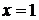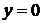Рис. 10
IV. Фигура, заключённая между двумя криволинейными трапециями.
Рис. 11
Площадь фигуры, заключённой между двумя криволинейными трапециями, вычисляется по формуле 
.
Пример. Вычислим площадь фигуры, ограниченной линиям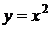и 
и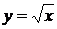 
.
Рис. 12
.
V. Криволинейная трапеция, стоящая на оси 
- фигура, ограниченная графиком функции 
, осью и прямыми 
, 
.
|
|
|
Площадь такой фигуры вычисляется по формуле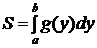 
.
Несобственные интегралы I рода
К несобственным интегралам I рода относятся интегралы от непрерывных функций с бесконечными пределами интегрирования: интегралы вида 
, 
и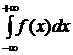 
.
Несобственный интеграл от функции 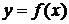, определённой на промежутке 
и интегрируемой по любому отрезку , вычисляется через предел интеграла 
при 
: 
.
Аналогично вычисляется несобственный интеграл : 
.
Примеры:1) 
;
2) 
;
3) 
.
Если предел 
конечен, то несобственный интеграл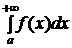 
называется сходящимся, в противном случае - расходящимся. Аналогичные определения справедливы для интеграла 
. Таким образом, несобственный интеграл примера 1 расходящийся, а интегралы примеров 2, 3 – сходящиеся.
Несобственный интеграл с двумя бесконечными пределами вычисляется как сумма двух несобственных интегралов с одним бесконечным пределом интегрирования: 
, где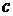 
- это любое действительное число. Несобственный интеграл 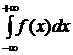с двумя бесконечными пределами сходится, если являются сходящимися оба несобственных интеграла 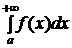и , и расходится, если хотя бы один из интегралов 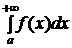или расходящийся.
Пример: 
. Интеграл сходится.
ВОПРОСЫ ДЛЯ ЗАЧЁТА
|
|
|
1. Основные периоды развития математики.
2. Аксиоматический метод.
3. Числовые последовательности. Предел числовой последовательности. Свойства пределов. Ограниченные, бесконечно малые, бесконечно большие, сходящиеся и расходящиеся числовые последовательности.
4. Определение функции. Предел числовой функции. Основные теоремы о пределах функций. Замечательные пределы.
5. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций. Список основных эквивалентностей.
6. Правила вычисления пределов числовых последовательностей и функций.
7. Непрерывность функции. Классификация точек разрыва.
8. Определение производной функции в точке. Таблица производных.
9. Правила дифференцирования.
10. Правила Лопиталя.
11. Геометрический смысл производной. Касательная и нормаль к плоской кривой. Экономические интерпретации производной.
12. Производные высших порядков. Дифференциалы. Дифференцирование функций, заданных неявно и параметрически.
13. Определение производной функции в точке. Таблица производных.
14. Основные теоремы дифференциального исчисления: теоремы Ферма, Ролля, Лагранжа, Коши.
15. Формулы Тейлора и Маклорена. Разложение по формуле Маклорена основных элементарных функций: ,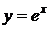 
, 
, 
, 
.
|
|
|
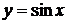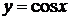16. Нахождение асимптот графика функции.
17. Нахождение промежутков выпуклости и вогнутости функции. Точки перегиба.
18. Схема исследования функции с помощью производной.
19. Задачи на наибольшее и наименьшее значения функции на промежутке.
20. Функции двух переменных: определение, область определения, множество значений. Линии уровня функции от двух переменных.
21. Предел и непрерывность функции от двух переменных. Частные производные функции двух переменных. Экономическое приложение частных производных.
22. Экстремумы функции двух переменных.
23. Условный экстремум функции двух переменных.
24. Понятие неопределенного интеграла. Таблица неопределенных интегралов.
25. Правила интегрирования. Интегрирование методами разложения и замены переменной.
26. Метод интегрирования по частям.
27. Интегрирование дробно-рациональных функций: интегрирование простейших дробей.
28. Метод неопределенных коэффициентов (интегрирование сложных дробей с помощью простейших).
29. Определенный интеграл. Свойства определенного интеграла.
30. Приложения определенного интеграла к вычислению площадей плоских фигур.
31. Несобственные интегралы первого рода.
|
|
|
32. Несобственные интегралы второго рода. Признаки сходимости несобственных интегралов.
Дата добавления: 2018-06-01; просмотров: 257; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!