Алгоритм исследования функций от двух переменных на экстремум
1.Вычислить частные производные первого порядка:  и
и  . Из системы
. Из системы  найти точки, подозрительные на экстремум (стационарные точки). Пусть
найти точки, подозрительные на экстремум (стационарные точки). Пусть  - стационарная точка функции
- стационарная точка функции  (таких точек может быть несколько).
(таких точек может быть несколько).
2.Вычислить частные производные второго порядка  ,
,  ,
,  и их значения в стационарной точке:
и их значения в стационарной точке: 
3.Найти значение дискриминанта  .
.
а) Если  , то в точке
, то в точке  экстремум есть, при этом, если
экстремум есть, при этом, если 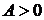 (или
(или  при
при 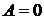 ), то в точке
), то в точке  функция имеет минимум, а если
функция имеет минимум, а если  (или
(или  при
при 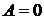 ) – максимум.
) – максимум.
б) Если  , то в точке
, то в точке  экстремума нет.
экстремума нет.
в) Если  , то требуются дополнительные исследования.
, то требуются дополнительные исследования.
Примеры. Найдём экстремумы функций:
1)  .
.
1. Вычислим частные производные первого порядка:  ,
,  . Из системы
. Из системы  находим точку
находим точку  , подозрительную на экстремум.
, подозрительную на экстремум.
2. Найдём частные производные второго порядка:  ,
,  ,
,  . Значения вторых производных не зависят от
. Значения вторых производных не зависят от 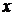 и
и 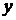 , поэтому нет необходимости вычислять их величину в стационарной точке и
, поэтому нет необходимости вычислять их величину в стационарной точке и  ,
,  ,
,  .
.
3. Вычисляем значение дискриминанта  . Следовательно, в точке
. Следовательно, в точке  нет экстремума.
нет экстремума.
2) .
.
1. Частные производные первого порядка равны  ,
,  . Точка
. Точка  - стационарная точка, так как её координаты являются решением системы
- стационарная точка, так как её координаты являются решением системы 
2. Частные производные второго порядка равны  ,
,  ,
,  . Вычислим их значения в стационарной точке:
. Вычислим их значения в стационарной точке:  ,
,  ,
,  .
.
3. Дискриминант равен  . Следовательно, в точке
. Следовательно, в точке  экстремум есть. Так как
экстремум есть. Так как  ,
,  - точка минимума,
- точка минимума,  .
.
3) 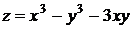 .
.
1. Вычислим частные производные первого порядка: 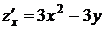 ,
,  . Находим стационарные точки, используя необходимые условия:
. Находим стационарные точки, используя необходимые условия:  ,
,  ,
,  ;
;  ,
,  . Следовательно,
. Следовательно,  ,
, 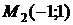 - стационарные точки.
- стационарные точки.
|
|
|
2. Находим вторые частные производные: 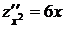 ,
,  ,
, 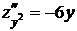 и их значения в стационарных точках:
и их значения в стационарных точках: 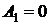 ,
, 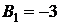 ,
,  ;
;  ,
,  ,
,  .
.
3.  . Следовательно, в точке
. Следовательно, в точке  нет экстремума.
нет экстремума.
 . Следовательно, в точке
. Следовательно, в точке 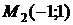 экстремум есть. Так как
экстремум есть. Так как  ,
,  - точка максимума,
- точка максимума,  .
.
4)  .
.
1. Вычисляем частные производные первого порядка:  ,
,  . Из системы
. Из системы  находим стационарные точки:
находим стационарные точки:

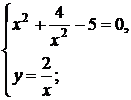 ,
, 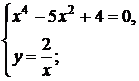
 ,
, 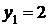 ;
;  ,
,  ;
;  ,
,  ;
;  ,
,  . Следовательно,
. Следовательно, 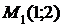 ,
,  ,
, 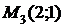 ,
,  - точки, подозрительные на экстремум.
- точки, подозрительные на экстремум.
2. Находим вторые частные производные: 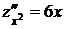 ,
,  ,
,  и их значения в стационарных точках:
и их значения в стационарных точках: 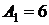 ,
,  ,
,  ;
;  ,
,  ,
,  ;
;  ,
,  ,
,  ;
;  ,
, 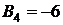 ,
,  .
.
3. Вычисляем значения всех дискриминантов и делаем выводы.  . Следовательно, в точке
. Следовательно, в точке  нет экстремума.
нет экстремума.
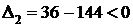 , поэтому в точке
, поэтому в точке  нет экстремума.
нет экстремума.
 . Следовательно, в точке
. Следовательно, в точке 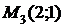 экстремум есть. Так как
экстремум есть. Так как 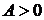
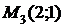 - точка минимума,
- точка минимума,  .
.
 , поэтому в точке
, поэтому в точке  экстремум есть. Так как
экстремум есть. Так как 
 - точка максимума,
- точка максимума,  .
.
Тема 3. ИНТЕРАЛЬНОЕ ИСЧИСЛЕНИЕ
Основная задача дифференциального исчисления заключается в нахождении производной от заданной функции. Интегральное исчисление решает обратную задачу: дана функция 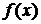 , требуется найти функцию
, требуется найти функцию  , такую, что
, такую, что 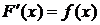 . Функция
. Функция  при этом называется первообразной для функции
при этом называется первообразной для функции 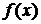 .
.
Определение 11.Функция  называется первообразной для функции
называется первообразной для функции 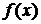 на промежутке
на промежутке 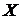 , если в каждой точке
, если в каждой точке 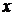 этого промежутка справедливо равенство
этого промежутка справедливо равенство 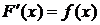 .
.
|
|
|
Пример. Найдём первообразные для функции  .
.  ,так как
,так как  . Функции
. Функции  и
и также являются первообразными для функции
также являются первообразными для функции  . Вообще, любая функция вида
. Вообще, любая функция вида 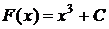 , где
, где  , является первообразной для функции
, является первообразной для функции  .
.
Вывод: Если функция  - первообразная для функции
- первообразная для функции 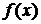 , то любая функция вида
, то любая функция вида  , где
, где  , также является первообразной для
, также является первообразной для 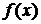 .
.
Совокупность всех первообразных для функции 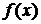 называется неопределённым интегралом от функции
называется неопределённым интегралом от функции 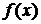 и обозначается
и обозначается  :
:
 , где
, где  .
.
Для вычисления неопределённых интегралов используют таблицу основных интегралов, правила интегрирования и методы интегрирования.
Таблица неопределенных интегралов
1. 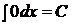 , где
, где  .
.
2.  ,
,  .
.
3.  , где
, где  ,
,  .
.
4.  ,
,  .
.
5.  ,
,  .
.
6.  , где
, где 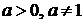 ,
,  .
.
7.  ,
,  .
.
8.  ,
,  .
.
9.  ,
,  .
.
10.  ,
,  .
.
11.  ,
,  .
.
12.  ,
,  .
.
13. 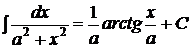 , где
, где  ,
,  .
.
14.  , где
, где  ,
,  .
.
15.  , где
, где 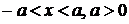 ,
,  .
.
16.  , где
, где  ,
,  .
.
Правила интегрирования
1.  .
.
2. 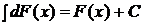 , где
, где  .
.
3. Постоянный множитель можно выносить за знак неопределённого интеграла:
 , где
, где 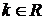 .
.
4. Интеграл суммы (разности) двух функций равен сумме (разности) интегралов этих функций:
 .
.
Дата добавления: 2018-06-01; просмотров: 389; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
