Схема исследования и построения графика функции
1. Найти область определения функции.
2. Исследовать функцию на четность-нечётность.
3. Найти точки пересечения графика функции с осями координат.
4. Отыскать асимптоты графика функции.
5. Найти интервалы монотонности и точки экстремума.
6. Найти интервалы выпуклости-вогнутости графика функции и точки перегиба.
7. Построить график, учитывая проведенные выше исследования и, если необходимо, вычисляя значения функции в дополнительных точках.
Остановимсяподробнее на 5 и 7 пунктах.
Определение 6. Прямая линия  называется асимптотой графика функции
называется асимптотой графика функции 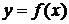 , если расстояние от точки
, если расстояние от точки  , лежащей на графике, до прямой
, лежащей на графике, до прямой  стремится к нулю при неограниченном удалении этой точки от начала координат (т.е. при стремлении хотя бы одной из координат точки к бесконечности).
стремится к нулю при неограниченном удалении этой точки от начала координат (т.е. при стремлении хотя бы одной из координат точки к бесконечности).
Асимптоты делятся на вертикальные, горизонтальные и наклонные.
1) нахождение вертикальных асимптот: прямая 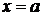 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 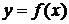 , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений  или
или  равно
равно 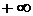 или
или 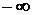 . Вертикальные асимптоты существуют в точках разрыва функции либо на границе области определения функции.
. Вертикальные асимптоты существуют в точках разрыва функции либо на границе области определения функции.
2) нахождение горизонтальных асимптот: прямая  является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции 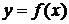 , если
, если  или
или  .
.
3) нахождение наклонных асимптот:
а) прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 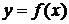 при
при  , если одновременно существуют пределы:
, если одновременно существуют пределы:  ,
,  ;
;
б) прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 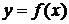 при
при  , если одновременно существуют пределы
, если одновременно существуют пределы  ,
,  .
.
|
|
|
Исследование графика функции на выпуклость и вогнутость (выпуклость вверх-вниз) производится аналогично изучению монотонности и точек экстремума только с применением второй производной.
Определение 7.График функции  называется выпуклым вверх (вниз) на промежутке
называется выпуклым вверх (вниз) на промежутке 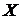 , если он расположен выше (ниже) любой касательной к графику функции, проведенной в любой точке этого промежутка.
, если он расположен выше (ниже) любой касательной к графику функции, проведенной в любой точке этого промежутка.
Достаточным условием выпуклости вверх (вниз) графика функции является следующая теорема: если функция  имеет на интервале
имеет на интервале 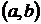 вторую производную и
вторую производную и  (
(  ) на
) на 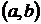 , то график функции имеет на интервале
, то график функции имеет на интервале 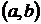 выпуклость вверх (вниз).
выпуклость вверх (вниз).
Пример. Определим интервалы выпуклости-вогнутости графика функции 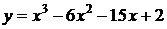 .
.
Область определения функции – множество всех действительных чисел  . Вторая производная функции равна
. Вторая производная функции равна  . Находим критические точки второго рода (точки, в которых вторая производная обращается в ноль или не существует):
. Находим критические точки второго рода (точки, в которых вторая производная обращается в ноль или не существует): 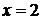 . Разбиваем область определения функции на интервалы критическими точками второго рода и методом пробных точек исследуем знаки второй производной на каждом из интервалов.
. Разбиваем область определения функции на интервалы критическими точками второго рода и методом пробных точек исследуем знаки второй производной на каждом из интервалов.

Рис. 1
Функция выпукла вверх при  , выпукла вниз при
, выпукла вниз при 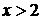 .
.
|
|
|
Определение 8.Если в точке  график функции
график функции  имеет касательную и при переходе через неё выпуклость вверх меняется на выпуклость вниз или наоборот, то точка
имеет касательную и при переходе через неё выпуклость вверх меняется на выпуклость вниз или наоборот, то точка  называется точкой перегиба.
называется точкой перегиба.
Необходимым условием точки перегиба является следующая теорема: если функция  имеет в точке
имеет в точке 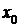 непрерывную вторую производную и в точке
непрерывную вторую производную и в точке  есть перегиб графика этой функции, тогда
есть перегиб графика этой функции, тогда  .
.
Достаточное условие точки перегиба имеет вид: пусть функция  имеет вторую производную в некоторой окрестности точки
имеет вторую производную в некоторой окрестности точки 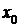 и при переходе через точку
и при переходе через точку 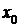 слева направо производная
слева направо производная  меняет знак, тогда график функции
меняет знак, тогда график функции  имеет перегиб в точке
имеет перегиб в точке  .
.
Таким образом, точки перегиба следует искать среди точек области определения, в которых вторая производная обращается в ноль. При переходе через точку перегиба вторая производная обязана сменить знак.
Пример.Определим точки перегиба функции 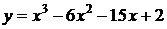 . Вторая производная обращается в ноль при
. Вторая производная обращается в ноль при 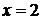 . Функция имеет вторую производную в окрестности точки
. Функция имеет вторую производную в окрестности точки 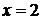 и при переходе через неё меняет свой знак. Следовательно,
и при переходе через неё меняет свой знак. Следовательно, 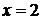 - точка перегиба графика функции
- точка перегиба графика функции 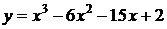 .
.
Пример. Исследуем и построим график функции  .
.
1. Область определения функции:  .
.
2. Функция нечётная, так как  .
.
|
|
|
3. Точки пересечения с осью  ищем из уравнения
ищем из уравнения 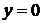 или
или  . Последнее уравнение не имеет корней, поэтому точек пересечения с осью
. Последнее уравнение не имеет корней, поэтому точек пересечения с осью  нет. График функции не имеет пересечений и с осью
нет. График функции не имеет пересечений и с осью  , так как
, так как  .
.
4. Асимптоты:
1) вертикальные: точкой разрыва графика функции является 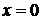 .
.  , следовательно, прямая
, следовательно, прямая 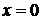 является вертикальной асимптотой.
является вертикальной асимптотой.
2) горизонтальные:  . Следовательно, горизонтальных асимптот нет.
. Следовательно, горизонтальных асимптот нет.
3) наклонные:
а)  ,
,  ;
;
 ,
,  .
.
Следовательно, прямая  - наклонная асимптота при
- наклонная асимптота при  .
.
б) Аналогично, прямая  - наклонная асимптота при
- наклонная асимптота при  .
.
5. Исследуем функцию на монотонность и точки экстремума. Производная функции равна  . Производная обращается в ноль в точках
. Производная обращается в ноль в точках  .
.
 |
Рис. 2
 Функция возрастает при
Функция возрастает при  и
и  , убывает при
, убывает при  и
и 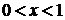 . Точка
. Точка  является точкой минимума,
является точкой минимума,  ;
;  является точкой максимума,
является точкой максимума, 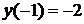 .
.
6. Проведем изучение промежутков выпуклости вверх-вниз функции и точек перегиба. Вторая производная функции равна  . Вторая производная не обращается в ноль.
. Вторая производная не обращается в ноль.
 |
Рис. 3
Функция выпукла вверх при  , выпукла вниз при
, выпукла вниз при  . Точек перегиба нет.
. Точек перегиба нет.
7. Построим график функции, учитывая проведённые выше исследования и вычисляя значения функции в дополнительных точках.
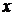
| 0,5 | -0,5 | 2 | -2 |
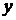
| 2,5 | -2,5 | 2,5 | 2,5 |
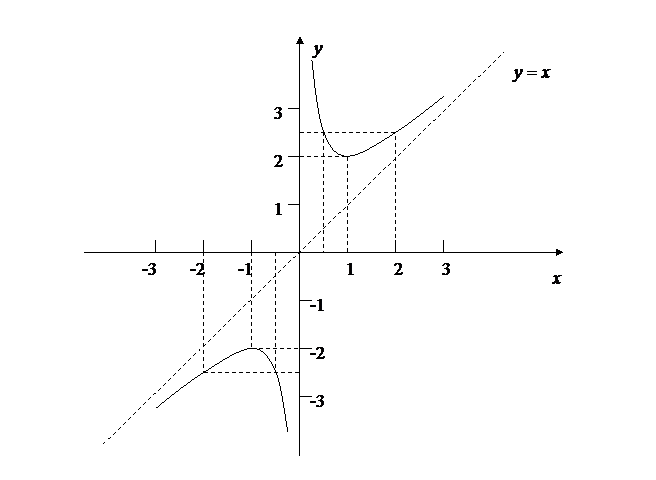 Рис. 4
Рис. 4
|
|
|
Дата добавления: 2018-06-01; просмотров: 234; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
