Правила вычисления пределов последовательностей и функций
1.Подставить бесконечность вместо 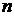 или предельное значение
или предельное значение 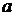 вместо
вместо 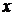 в выражение, стоящее за знаком предела.
в выражение, стоящее за знаком предела.
Например, 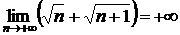 ,
,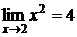 .
.
Важно, что 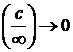 , где
, где 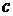 - любое число.
- любое число. 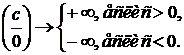
Если в результате подстановки получилось число или 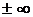 , то это ответ. Очень часто после подстановки получаются неопределенности вида
, то это ответ. Очень часто после подстановки получаются неопределенности вида 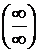 ,
,  ,
, 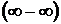 ,
, 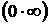 ,
, 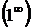 .
.
2.Если получилась неопределённость вида 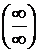 , то можно:
, то можно:
а) разделить числитель и знаменатель дроби на старший член (на наивысшую степень или на наибольшее число в степени).
Примеры:1)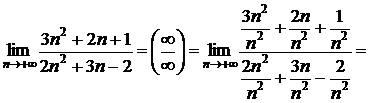
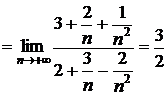 .
.
Вывод: Если под знаком предела стоит дробь, в числителе и знаменателе которой многочлены одинаковых степеней, то предел равен отношению коэффициентов при старших степенях.
2) 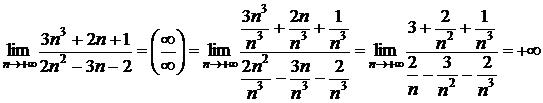 ;
;
3) 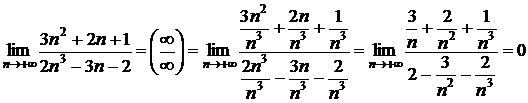 ;
;
4) 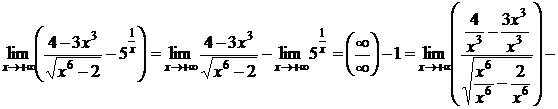
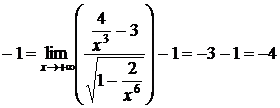 ;
;
5)  ;
;
6) 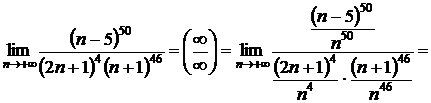
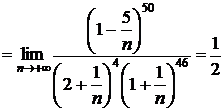 .
.
б) воспользоваться правилом Лопиталя: 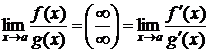 .
.
Пример: 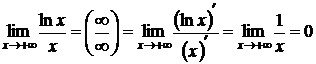 .
.
3. Если получилась неопределённость вида  , то можно:
, то можно:
а) сократить на выражение 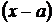 , которое стремится к нулю.
, которое стремится к нулю.
Примеры:1)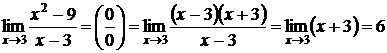 ;
;
2)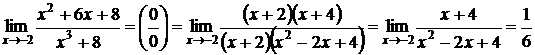 .
.
б) бесконечно малый множитель заменить на эквивалентный: при 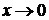
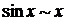 ,
, 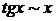 ,
, 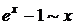 ,
, 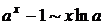 ,
, 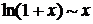 ,
, 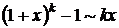 , где
, где 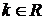 ,
, 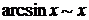 ,
, 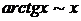 ,
, 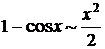 .
.
Пример: 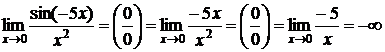 .
.
в) воспользоваться правилом Лопиталя: 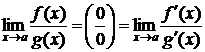 .
.
Пример: 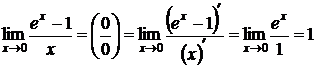 .
.
г) домножить и разделить на сопряжённое, если выражение, стоящее за знаком предела, имеет корни.
Пример: 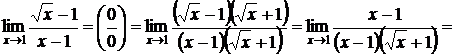
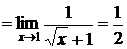 .
.
4.Если получились неопределённости вида 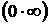 или
или 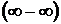 , то их нужно свести к неопределённостям
, то их нужно свести к неопределённостям 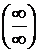 или
или  .
.
Примеры:1) 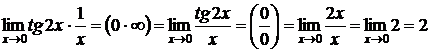 ;
;
2)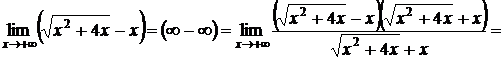
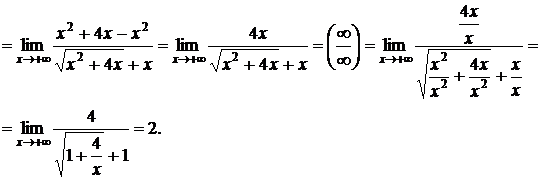
5.Если получилась неопределённость вида 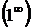 , то нужно использовать второй замечательный предел:
, то нужно использовать второй замечательный предел: 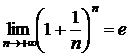 ,
, 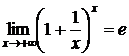 ,
, 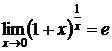 .
.
Примеры: 1) 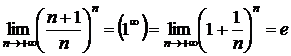 ;
;
2) 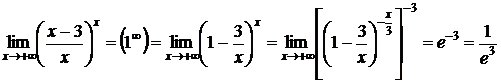 ;
;
3) 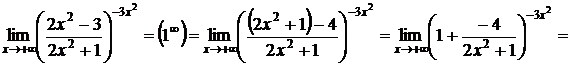
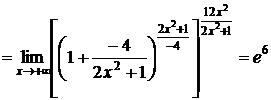 ;
;
4) 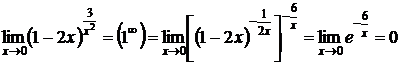 .
.
Тема 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
|
|
|
Дифференциальное исчисление занимается изучением и приложениями производных. Рассмотрим основные моменты этого раздела сначала применительно к функциям одной переменной, а затем - к функциям нескольких переменных.
I. Функции от одной переменной.
Определение 4.Производной функции 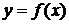 в точке
в точке 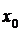 называется предел отношения приращения
называется предел отношения приращения 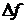 функции в точке
функции в точке 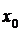 к приращению аргумента
к приращению аргумента 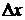 при
при 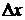 стремящемся к нулю, если этот предел существует. Производная функции
стремящемся к нулю, если этот предел существует. Производная функции 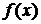 в точке
в точке 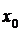 обозначается
обозначается 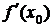 :
:
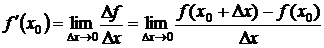 .
.
Производную функции 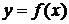 в точке
в точке 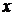 обозначают
обозначают 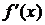 ,
, 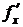 ,
, 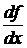 или
или 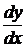 .
.
Необходимым условием существования производной функции в заданной точке является непрерывность функции в этой точке (функция называется непрерывной в точке 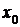 , если она определена в окрестности данной точки и
, если она определена в окрестности данной точки и 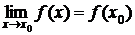 ). Обратное утверждение является неверным. Например, функция
). Обратное утверждение является неверным. Например, функция 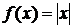 непрерывна на промежутке
непрерывна на промежутке 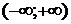 , но в точке
, но в точке 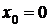 производной не имеет.
производной не имеет.
Операция нахождения производной функции называется дифференцированием. Функция, имеющая производную в точке 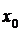 , называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке интервала
, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке интервала 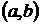 , называется дифференцируемой на этом интервале.
, называется дифференцируемой на этом интервале.
Для вычисления производных используется таблица производных и правила дифференцирования.
|
|
|
Таблица производных
1. 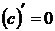 , где
, где 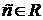 .
.
2. 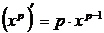 , где
, где 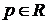 .
.
3. 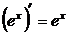 .
.
4. 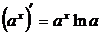 , где
, где 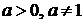 .
.
5. 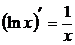 .
.
6. 
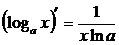 , где
, где 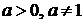 .
.
7. 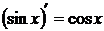 .
.
8. 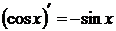 .
.
9. 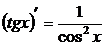 .
.
10. 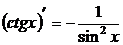 .
.
11. 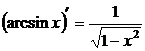 .
.
12. 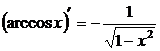 .
.
13. 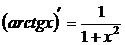 .
.
14. 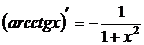 .
.
Правила дифференцирования
1. Постоянный множитель можно выносить за знак производной:
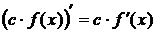 , где
, где 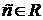 .
.
Пример: 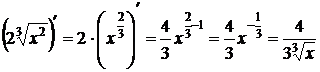 .
.
2. Производная суммы (разности) двух функций, определённых на одном и том же промежутке, равна сумме (разности) производных этих функций:
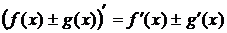 .
.
Пример: 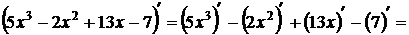
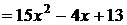 .
.
3. Производная произведения двух функций, определённых на одном и том же промежутке, вычисляется по формуле
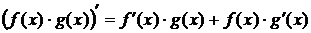 .
.
Пример: 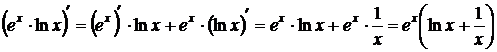 .
.
4. Если функции 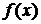 и
и 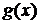 имеют в точке
имеют в точке 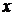 производные и
производные и 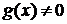 , то в этой точке существует производная их частного, которая вычисляется по формуле
, то в этой точке существует производная их частного, которая вычисляется по формуле
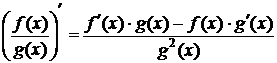 .
.
Пример: 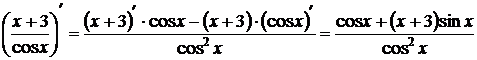 .
.
5. Если функция сложная, то есть 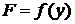 , где
, где 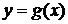 , то её производная может быть вычислена по правилу
, то её производная может быть вычислена по правилу
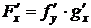 .
.
Пример: 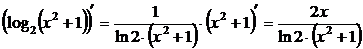 .
.
Определение 5.Производной второго порядка (второй производной) функции 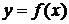 называется производная от её производной:
называется производная от её производной:
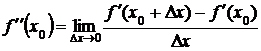 ,
,
если этот предел существует.
Аналогично производную от второй производной называют производной третьего порядка или третьей производной.
В общем случае производной 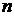 порядка называется производная от производной
порядка называется производная от производной 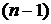 порядка:
порядка: 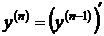 .
.
|
|
|
Производные второго, третьего и более высоких порядков вычисляются последовательным дифференцированием заданной функции.
Примеры: 1) 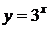 ,
, 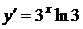 ,
, 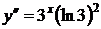 ,
, 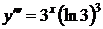 , … ,
, … , 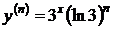 .
.
2) 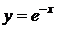 ,
, 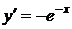 ,
, 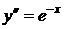 ,
, 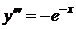 , … ,
, … , 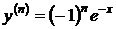 .
.
С помощью пределов и производных производится исследование графиков функций. Изучение графика функции целесообразно производить по следующему плану.
Дата добавления: 2018-06-01; просмотров: 382; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
