Интеграл. Дифференциальные уравнения.

⇐ ПредыдущаяСтр 5 из 9Следующая ⇒

Нахождение производных и нахождение неопределенных интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия

Решить интеграл – это значит найти определенную функцию 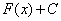, пользуясь некоторыми правилами, приемами и таблицей.

Любой неопределенный интеграл имеет вид:

– значок интеграла.

– подынтегральная функция – значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.

– подынтегральное выражение

– первообразная функция.

– множество первообразных функций, в любом неопределенном интеграле к ответу приплюсовывается константа .

Таблица основных неопределенных интегралов.

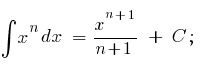
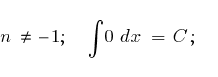
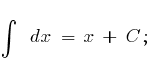
Основные методы интегрирования

u, v, w - это функции от x; c - постоянная.

Пример 1

(1) Используем формулу квадрата суммы , избавляясь от степени.

(2) Вносим в скобку, избавляясь от произведения.

(3) Используем свойства линейности интеграла (оба правила сразу), выносим постоянный множитель за знак интеграла, и записываем в виде суммы интегралов.

(4) Превращаем интегралы по табличной формуле .

(5) Упрощаем ответ. Здесь следует обратить внимание на обыкновенную неправильную дробь – она несократима и в ответ входит именно в таком виде.

Решить определенный интеграл – это значит, найти число с помощью формулы Ньютона-Лейбница:

Этапы решения определенного интеграла:

1) Находим первообразную функцию (неопределенный интеграл), константа в определенном интеграле не добавляется. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла.

2) Подставляем значение верхнего предела в первообразную функцию: .

3) Подставляем значение нижнего предела в первообразную функцию: .

4) Рассчитываем разность , то есть, находим число.

Пример2

Вычислить определенный интеграл

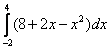
Решение:

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

Можно сразу записать

Ответ. 36

Определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры

Криволинейной трапецией называется плоская фигура, ограниченная осью 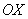,прямыми , и графиком непрерывной на отрезке функции , которая не меняет знак на этом промежутке. Пусть данная фигура расположена ненижеоси абсцисс:

Тогда площадь криволинейной трапеции численно равна определенному интегралу ..

Пример 3

Вычислить площадь фигуры, ограниченной линиями 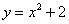, , , осью абсцисс.

Выполним чертеж , ось абсцисс- ось ОХ.

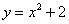На отрезке график функции расположен над осью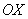, поэтому:

Ответ:

Дифференциальные уравнения

Решить дифференциальное уравнение – это значит, найти множество всех функций, которые удовлетворяют данному уравнению. Такое множество функций часто имеет вид ( – произвольная постоянная), который называется общим решением дифференциального уравнения.

Дифференциальное уравнение первого порядка имеет вид F(x, y,y’,y’’) = 0
первая производная функции: y’ = dy/dx

Способ- разделить переменные. В левой части оставить только «игреки», а в правой части только «иксы». Разделение переменных выполняется с помощью: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п. Затем - интегрирование дифференциального уравнения

Пример 4Решить диф. уравнение (У-11)dx – (X+25)dу =0

– (X+25)dу = -(У-11)dх

(X+25)dу = (У-11)dх

dу = (У-11)dх/ (X+25)

dу/(У-11) = dх/ (X+25)

∫dу/(У-11) = ∫dх/ (X+25) Воспользуемся формулой

, вместо х можно записать( х+любое число), получаем

Ln(y-11) = Ln(x+25)+LnC по свойствам логарифмов имеем

Ln(y-11) = Ln(x+25)∙C

(y-11) = (x+25)∙C

y = (x+25)∙C +11 - общее решение дифференциального уравнения.

Ответ. y = (x+25)∙C +11

В дифференциальное уравнение второго порядка обязательно входит вторая производная у’’
F(x, y,y’,y’’) = 0

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:y’’ + py’ + qy = 0, где p иq – константы (числа), а в правой части – строго ноль.

Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

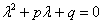
вместо второй производной записываем ;
вместо первой производной записываем просто «лямбду»;
вместо функции ничего не записываем.

Если характеристическое уравнение 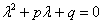имеет два различных действительных корня 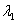, (т.е., если дискриминант ), то общее решение однородного уравнения выглядит так:
, где – константы.