Определители второго и третьего порядка

Определителем второго порядка называется число .

Определителем третьего порядка называется число

Пример1

Ответ. 15

Пример 3Вычислить определитель:

Решение:
Воспользуемся правилом треугольников.
Объясним картинку подробно, т.е. распишем каждое слагаемое отдельно:

 

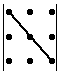
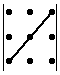
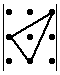
Ответ: 108

Решение систем линейных уравнений методом определителей (метод Крамера)

Рассмотрим систему уравнений

Вычислим определитель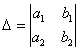 ,его называют главным определителем системы.

Если , то система имеет бесконечно много решений или несовместна (не имеет решений).

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 4Решить систему линейных уравнений
Решение:

,значит, система имеет единственное решение.

;

;

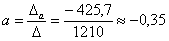
Ответ: ,

Оба корня обладают бесконечными хвостами, и найдены приближенно.

Обязательным для оформления задания является: «≠0, значит, система имеет единственное решение».

 

Рассмотрим систему трех линейных уравнений с тремя неизвестными: x₁, x₂, x₃:

(коэффициенты a_ij и свободные члены b_i считаются заданными).

Решение: составим определители :

, , , ,

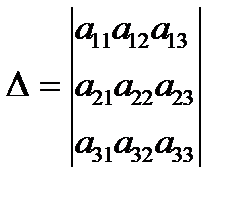где D называют определителем системы, а определители Dx_i получены из основного определителя D заменой свободными членами b_i элементов соответствующего столбца.

 

Особые случаи:

1) если D¹ 0, то система имеет единственное решение;

2) если D = 0, Dx_i¹ 0, то система несовместна;

3) если D = Dx_i= 0, то система либо имеет бесконечное множество решений, либо она решений не имеет.

Пример 5

Решить систему линейных уравнений:

Решение: составим определители D, D_x, D_y, D_z и найдем их значения.

 

=1∙1∙(-1)+(-2)∙7∙2+3∙(-3)∙(-3) -2∙1∙(-3) -3∙(-2)∙(-1) -7∙(-3)∙1= -1 -28+27+6-6+21            

(D¹ 0, следовательно, система имеет единственное решение).

.   .    .

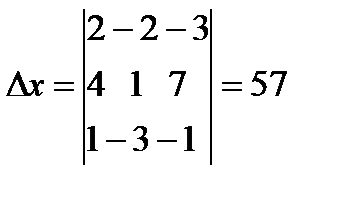Найдем решение системы:                                     

Ответ: (3; 2; –1).

Аналитическая геометрия

Задача (пример с разбором решения и основными формулами)

Заданы точки A(0, 1), B(1, −1), C(5, 0). Требуется:

1 Начертить треугольник ABC .

2 Найти координаты векторов А͞В и А͞С

3 Найти длины сторон AB, AC , BC .

4 Найти угол BAC треугольника.

5 Найти площадь треугольника ABC .

6 Составить уравнения прямых AB, AC , BC .

Решение:        

1. Начертить треугольник ABC на системе координат, взяв за единичный отрезок две клетки или 1 см

2.Найти координаты векторовА͞В иА͞С, иВ͞С

Используется формула:

Формула (координаты вектора – из координат конца вектора вычесть координаты начала)

AB = (x _B − x _A ,y_B − y _A )

AB = (1 − 0,−1 − 1) = (1,−2)ВА = (-1, 2)

AC = (5 − 0,0 − 1) = (5,−1) СА = (-5, 1)

ВС =(5- 1 ,0-(-1) ) = (4, 1)СВ = (-4, -1)

3. Найти длины сторон AB , AC , BC

Используется формула. Длина вектора вычисляется по формуле а =√х² + у²

Координаты векторов берем из шага 2.

АВ=√1² + (-2)² = √5 =2,236

АС = √5² + (-1)² = √26 = 5,099

ВС = √42 + 12 = √17 =4,123     или

Используется формула (расстояние между точками)

AB =√͞ (͞x_B ͞−͞ x ͞_A ͞) ² ͞+͞ (͞y ͞_B ͞−͞ y ͞_A )²

AB =√(1 − 0) ² + (−1 − 1) ² =√ 5 = 2.236

AC =√(5 − 0) ² + (0 − 1) ² =√ 26 = 5.099

BC =√(5 − 1) ² + (0 − (−1)) ² =√ 17 = 4.123

4. Найти угол ∠BAC

Используются формулы:

Формула (чтобы найти угол можно найти косинус угла)  

cos∠BAC=(AB·AC)/ (AB·AC) ,

---

Дата добавления: 2018-06-01; просмотров: 299; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!