Задачі для самостійного розв’язання
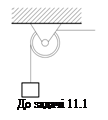Задача 11.1. При рівномірному опусканні вантажу масою М=2т зі швидкістю 
відбулася несподівана затримка верхнього кінця троса, на якому опускався вантаж, через защемлення троса в обоймі блока. Нехтуючи масою троса, визначити його найбільший натяг при наступних коливаннях вантажу, якщо коефіцієнт жорсткості троса 4·106Н/м.
Відповідь: 466,8кН.
Задача 11.2. До пружини жорсткістю с=2кН/м спочатку підвісили вантаж масою 6кг, а потім замінили його вантажем удвічі більшої маси. Визначити частоти і періоди коливань вантажів.
Відповідь: k1=18,26рад/с, k2=12,9рад/с, Т1=0,344с, Т2=0,49с.
Задача 11.3. Вантаж масою 
, підвішений до пружини, коефіцієнт жорсткості якої с=98Н/м, перебуває в рівновазі. У деякий момент до вантажу 
додали вантаж 
. Визначити рівняння руху і період коливань двох вантажів.
Відповідь: х0=–0,08cos5,916t м, Т=1,062с.
Задача 11.4. Вантаж підвісили спочатку до пружини жорсткістю 
, а потім до пружини жорсткістю 
. Знайти відношення частот і періодів коливань вантажу в цих двох випадках.
Відповідь: 
, 
.
Задача 11.5. Визначити період вільних коливань фундаменту машини, поставленого на пружний ґрунт, якщо маса фундаменту з машиною М=90т, площа підошви фундаменту 
, коефіцієнт жорсткості ґрунту 
, де 
– питома жорсткість ґрунту.
Відповідь: Т=0,089с.
Задача 11.6. Знайти період вільних вертикальних коливань корабля на спокійній воді, якщо маса корабля М т, площа його горизонтальної проекції S м2. Щільність води 
. Силами, обумовленими в'язкістю води, знехтувати.
|
|
|
Відповідь: 
.
Задача 11.7. Тіло масою m перебуває на похилій площині, яка утворює кут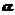 
з вертикаллю. До тіла прикріплена пружина, жорсткість якої с. Пружина паралельна похилій площині. Знайти рівняння руху тіла, якщо в початковий момент воно було прикріплене до кінця нерозтягнутої пружини і йому була надана початкова швидкість 
, напрямлена вниз по похилій площині. Початок координат взяти в положенні статичної рівноваги.
Відповідь: 
, де 
Задача 11.8. До однієї і тієї ж пружини підвісили спочатку вантаж вагою р, а іншого разу вантаж вагою 3р. Визначити, у скільки разів зміниться період коливань. Знаючи коефіцієнт жорсткості пружини с, а також початкові умови (вантажі підвішувалися до кінця нерозтягнутої пружини і опускалися без початкової швидкості), знайти рівняння руху вантажів.
Відповідь: 
, 
, 
.
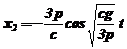Практичне заняття №12
Тема: Теореми про зміну кількості руху матеріальної точки та механічної системи. Теореми про зміну моменту кількості руху матеріальної точки та системи
|
|
|
Програмні питання
Кількість руху матеріальної точки. Імпульс сили. Теорема про зміну кількості руху матеріальної точки в диференціальній та інтегральній формах. Обчислення кількості руху системи. Теорема про зміну кількості руху системи.
Момент кількості руху точки відносно центра і осі. Головний момент кількості руху системи. Теореми про зміну моменту кількості руху матеріальної точки та системи.
Література
1. Курок В.П. Технічна механіка. Курс лекцій: навч. посіб. для студ. вищих навч. закл. – К.: Пед. преса, 2007. – 272с., л.30.
2. Тарг С.М. Краткий курс теоретической механики — М.: Высшая школа, 1986. – 461 с., §§ 83 – 85, 110 – 112, 115 – 117.
3. Никитин Е.М. Краткий курс теоретической механики — М.: Наука, 1983. – 400 с., §§ 83 – 88, 90 – 95.
4. Цасюк В.В. Теоретична механіка: Навчальний посібник. – К.: Центр навчальної літератури, 2004. – 402с., §§17.1 – 17.3, 21.4, 21.7 – 21.8.
5. Мещерский И.В. Сборник задач по теоретической механике. — М.: Наука, 1986. – 448 с.
Короткі теоретичні відомості
Кількістю руху матеріальної точки називається векторна величина 
, яка дорівнює добутку маси точки на її швидкість. Цей вектор напрямлений так само, як і швидкість точки, тобто по дотичній до її траєкторії. Одиниця вимірювання в системі СІ – 1кгּм/с=1 Нּс.
|
|
|
Для характеристики дії сили на тіло за деякий проміжок часу вводиться поняття імпульсу сили.
Елементарним імпульсом сили називається векторна величина 
, яка дорівнює добутку сили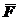 
на елементарний проміжок часу dt:
Елементарний імпульс напрямлений вздовж лінії дії сили.
Імпульс 
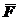будь-якої сили за кінцевий проміжок часу 
дорівнює:
.
Отже, імпульс сили за деякий кінцевий проміжок часу дорівнює визначеному інтегралу від елементарного імпульсу, взятому від нуля до .
Зокрема, якщо 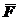– величина стала ( 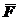=const), то:
Рівняння, що виражає теорему про зміну кількості руху в диференціальній формі:
Похідна від кількості руху матеріальної точки за часом дорівнює геометричній сумі всіх сил, що діють на точку.
Рівняння, що виражає теорему про зміну кількості руху точки в кінцевому вигляді:
Зміна кількості руху матеріальної точки за деякий проміжок часу дорівнює сумі імпульсів всіх сил, що діють на точку, за той же проміжок часу.
При розв'язанні задач замість векторного рівняння часто користуються рівняннями в проекціях:
Кількістю руху системи будемо називати векторну величину 
, яка дорівнює геометричній сумі (головному вектору) кількості руху всіх точок системи:
|
|
|
Кількість руху системи дорівнює добутку маси всієї системи на швидкість її центра мас:
Рівняння, що виражає теорему про зміну кількості руху системи в диференціальній формі:
Похідна за часом від кількості руху системи дорівнює геометричній сумі всіх зовнішніх сил, що діють на систему.
У проекціях на координатні осі маємо:
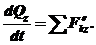
Рівняння, що виражає теорему про зміну кількості руху системи в інтегральній формі:
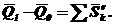
Зміна кількості руху системи за деякий проміжок часу дорівнює сумі імпульсів всіх зовнішніх сил, що діють на систему, за той же проміжок часу.
У проекціях на координатні осі будемо мати:
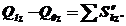
Із теореми про зміну кількості руху системи можна зробити висновки:
1. Якщо сума всіх зовнішніх сил, що діють на систему, дорівнює нулю:
тоді =const.
2. Якщо зовнішні сили, що діють на систему, такі, що сума їх проекцій на яку-небудь вісь (наприклад Oх) дорівнює нулю:
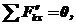
тоді Qx=const.
Ці результати і виражають закон збереження кількості руху системи.
Моментом кількості руху точки відносно деякого центра О називається векторна величина 
, яка визначається рівністю:
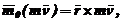
де 
– радіус-вектор точки, проведений із центра О.
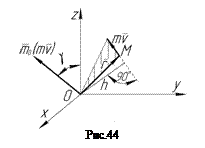Момент напрямлений перпендикулярно площині, яка проходить через і центр О, а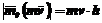 
(рис.44).
Момент кількості руху точки відносно якої-небудь осі Oz, яка проходить через центр О, буде дорівнювати проекції вектора на цю вісь:
де γ – кут між вектором і віссю Oz.
Теорема моментів для матеріальної точки відносно центра: похідна за часом від моменту кількості руху точки, взятого відносно якого-небудь нерухомого центра, дорівнює моменту сили, що діє на точку, відносно того ж центра:
Якщо спроектувати обидві частини останнього рівняння на яку-небудь вісь Oz, яка проходить через центр О, то дістанемо:
Це рівняння виражає теорему моментів відносно осі.
Головним моментом кількості руху (або кінетичним моментом) системи відносно центра О називається величина 
, яка дорівнює геометричній сумі моментів кількості руху всіх точок системи відносно цього центра:
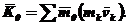
Кінетичний момент тіла, яке обертається, відносно осі обертання дорівнює добутку моменту інерції тіла відносно цієї осі на кутову швидкість тіла:
Теорема моментів для механічної системи: похідна за часом від головного моменту кількості руху системи відносно деякого нерухомого центра дорівнює сумі моментів всіх зовнішніх сил системи відносно цього ж центра:
Проектуючи обидві частини рівності на нерухомі осі Oxyz, дістанемо:
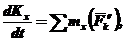
Приклади розв’язання задач
Задача 1. Тіло вагою Р=100Н рухається поступально вгору по негладенькій похилій площині, що утворює з горизонтом кут α=300, під дією сили 
, яка утворює з площиною кут β=450. Чому має дорівнювати модуль сили F для того, щоб через час t=10с після початку руху, швидкість тіла дорівнювала v=4м/с? Коефіцієнт тертя ковзання f=0,2 (рис. 45).
Розв’язання
Тіло, яке рухається поступально, розглядаємо як матеріальну точку С, в якій зосереджена вся маса тіла. На неї діють такі сили: сила ваги тіла 
, нормальна реакція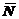 
площини, рушійна сила 
та сила тертя 
(див. рис. 45).
Вісь х напрямимо вздовж прямої, по якій рухається точка С.
Згідно теореми про зміну кількості руху точки:
. (1)
Оскільки сили, що діють на точку, сталі за величинами, то:
.
Для визначення нормальної реакції площини спроектуємо всі сили на вісь y:
,
звідки
, тоді 
.
За умовою задачі v0х=0, v1х=v.
Підставимо визначені значення сил у рівняння (1), будемо мати:
.
Розв’яжемо це рівняння з метою визначення сили F:
;
;
.
З останнього рівняння маємо:
Задача 2. Граната, яка летить зі швидкістю v=20м/с, розірвалась у повітрі на два осколки масами m1=6кг і m2=4кг. Швидкість більшого осколка збільшилась у напрямку руху до v1=40м/с. Знайти швидкість і напрямок руху меншого осколка.
Розв’язання
Частини гранати будемо розглядати як систему матеріальних точок. Напрямимо вісь х у бік руху гранати і запишемо рівняння, що виражає закон збереження кількості руху системи, в проекції на цю вісь:
,
де 
– маса всієї гранати.
З цього співвідношення знаходимо швидкість меншого осколка:
.
Знак «мінус» вказує на те, що менший осколок полетить у напрямку, протилежному руху гранати.
Задача 3. При обертанні барабана 1 масою m1 і радіусом r1 навколо нерухомої осі z на його бокову поверхню намотується нитка, яка рухає вантаж 2 масою m2, що ковзає по нерухомій горизонтальній площині (рис. 46). Обчислити головний момент кількості руху системи відносно осі z у залежності від кутової швидкості ω, а також кутове прискорення барабана, якщо до нього прикладений обертальний момент mоб, а коефіцієнт тертя ковзання вантажу об площину дорівнює f. Барабан вважати однорідним круглим диском. Масою нитки нехтуємо. Вісь z напрямлена перпендикулярно до площини рисунка.
Розв’язання
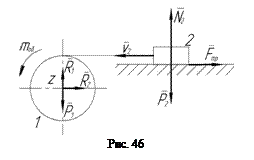До складу системи входять два твердих тіла: барабан і вантаж. Тому
,
де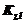 
– головний момент кількості руху барабана, а 
– головний момент кількості руху вантажу відносно нерухомої осі z.
Знайдемо 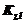за формулою 
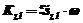, де 
– осьовий момент інерції барабана.
Головний момент кількості руху вантажу, який рухається поступально, визначається як момент кількості руху матеріальної точки. Тобто 
. Оскільки 
, то 
.
Тоді головний момент кількості руху системи відносно осі z:
(1)
Зобразимо всі зовнішні сили і момент системи: 
– сила ваги барабана, 
– сила ваги вантажу, 
і 
– складові реакції осі барабана, 
– нормальна реакція площини, – сила тертя ковзання та 
– обертальний момент (див. рис. 46).
Застосуємо теорему про зміну головного моменту кількості руху системи відносно осі z.
(2)
Враховуючи, що 
, 
, а сили 
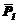, , прикладені в точці, яка лежить на осі z, маємо:
.
Визначаємо: 
.
Підставляючи попередні результати в рівняння (2) і розв’язуючи відносно ω', отримаємо кутове прискорення:
,
.
Питання для самоконтролю
1. Що називається кількістю руху матеріальної точки? Одиниці її вимірювання.
2. Дати означення елементарному імпульсу сили.
3. Чому дорівнює імпульс сили за кінцевий проміжок часу? У випадку 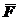= const?
4. Сформулювати та довести теорему про зміну кількості руху матеріальної точки.
5. Що називається кількістю руху системи ?
6. Вивести формулу визначення кількості руху системи.
7. Сформулювати і довести теорему про зміну кількості руху системи.
8. Викласти закон збереження кількості руху системи.
9. Дати означення моменту кількості руху точки відносно центра та осі.
10. Сформулювати і довести теорему про зміну моменту кількості руху точки відносно центра та осі.
11. Як визначається кінетичний момент системи відносно центра та осі?
12. Сформулювати та довести теорему про зміну кінетичного моменту системи.
Дата добавления: 2018-05-31; просмотров: 582; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!