Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса. Примеры.
Теорема Рисса.
Всякий линейный непрерывный функционал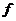 
в гильбертовом пространстве 
имеет вид 
, где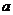 
- некоторый элемент из , однозначно определяемый функционалом 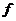. При этом 
.
Теорема Рисса означает, что сопряженное пространство 
изоморфно самому (т.е. можно установить взаимнооднозначное соответствие).
7.2. Общий вид линейного функционала в 
и 
( 
).
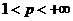№ 1 , 
изоморфно 
, где 
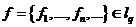
или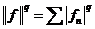 
.
№ 2. 
, 
изоморфно пространству 
всех ограниченных последовательностей с нормой 
, где 
.
№ 3 
- пространство стремящихся к нулю последовательностей 
с нормой 
изоморфно пространству
, 
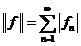
№ 4 
, 
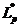изоморфно 
, где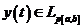 
.
№ 5. 
изоморфно пространству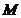 
- ограниченных на 
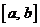функций, т. е. Функций, существенные максимумы которых конечны (почти всюду огранич. функций)
; где 
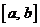- почти всюду на ограниченная функция и 
.
Заметим, что при 
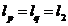и 
т.е. 
и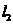 
- самосопряженные пространства, т.е. гильбертовы.
Определение линейного оператора. Примеры.
1.1. Определение линейного оператора.
Def оператор 
, определенный на пространстве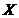 
и принимающий значения в пространстве 
, называется линейным, если этот оператор
1) аддитивен, т.е. 
.
2) Однороден, т.е. 
, 
.
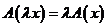В дальнейшем будем писать также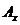 
1.2. Определение непрерывного оператора
Def Оператор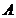 
называется непрерывным в точке 
, если 
при 
(здесь 
) или, что равносильно: если 
.
Def Если оператор непрерывен в каждой точке 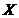, то говорят, что 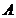непрерывен на .
|
|
|
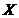Теорема. Если линейный оператор 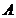, действующий из банахова пространства непрерывен в какой-либо одной точке банахова пространства 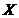, то он равномерно непрерывен на всем .
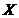1.3. Примеры линейных операторов
№ 1. Пусть 
, где 
- линейное нормированное пространство.
Такой оператор, переводящий каждый элемент пространства в себя, называется единичным оператором.
№ 2. Пусть 
, где 
непрерывная фиксированная функция, такой оператор называется оператором умножения на функцию , линейность оператора очевидна.
№ 3. Пусть 
- оператор дифференцирования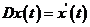 
, где 
-пространство непрерывно дифференцируемых функций на 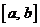с нормой 
.
№ 4. Общий вид линейного оператора, переводящего конечномерное пространство в конечномерное. Пусть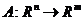 
, тогда 
, такой что 
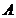. Ясно, что оператор определяется матрицей коэффициентов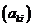 
Определение нормы оператора.
Def Пусть 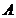- линейный ограниченный оператор. Наименьшая из постоянных 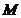, удовлетворяющих условию 
при всех 
называется нормой оператора 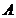и обозначается 
.
Равносильные определения 
.
Понятие обратного оператора.
Решение систем линейных алгебраических уравнений, линейных интегральных уравнений, а также некоторых задач для обыкновенных дифференциальных уравнений и уравнений с частными производными сводится к вопросу о существовании и единственности решения линейных операторных уравнений вида 
.
|
|
|
Пусть задан линейный оператор 
, причем, его область определения 
, а область значений 
.
Обратное отображение, обозначаемое 
, называется обратным оператором.
Предположим, что оператор 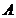отображает 
на 
взаимно однозначно. В этом случае существует обратный оператор отображающий взаимно однозначно на . В этом случае оператор также является линейным оператором.
Def Множество тех , для которых 
, называется ядром линейного оператора 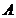и обозначается 
.
Теорема. Линейный оператор 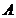переводит в взаимно однозначно 
когда 
.
Дата добавления: 2018-06-27; просмотров: 555; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!