Элементарные функции комплексного переменного.
Следующие функции (как однозначные, так и многозначные) называют основными элементарными функциями:
Дробно-рациональная функция
a)az+b, (а 
0, а, b 
C) – линейная функция;
б)zn , n N;– степенная функция с натуральным показателем;
в)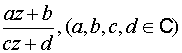 
– дробно-линейная функция;
г) функция Жуковского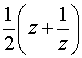 
.
2. Показательная функция:
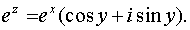
Наряду с введенным обозначением для показательной функции используют обозначение exp z.
Заметим, что на вещественной оси показательная функция комплексного переменного совпадает с показательной функцией действительного переменного. Непосредственная проверка убеждает, что на показательную функцию комплексного переменного переносится теорема сложения
Показательная функция комплексного переменного является периодической функцией с основным периодом 2pi, т. е.
.
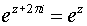3. Тригонометрические функции:
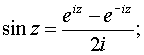
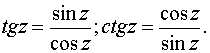
Для тригонометрических функций сохраняются теоремы сложения, а следовательно, и остальные формулы, справедливые для тригонометрических функций действительного переменного. Они являются периодическими функциями с теми же периодами, что и соответствующие тригонометрические функции действительного переменного.
Однако в случае комплексного переменного функции sinz, cosz ограниченными не являются.
4. Гиперболические функции:
Логарифмическая функция.
Логарифмическая функция Lnz, при z 0 определяется как обратная к показательной функции, причем
|
|
|
Так как показательная функция – периодическая с периодом 2pi, то логарифмическая функция является многозначной. В каждой точке z 0 она принимает бесконечно много значений.
Функция
где arg z – главное значение аргумента, называется главным значением логарифмической функции. Итак,
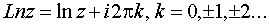
Известные правила о логарифме произведения и частного сохраняют свою силу и для многозначного логарифма, а именно: при z1 и z2, отличных от нуля, верны формулы
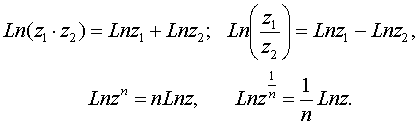
6. Общая степенная функция:
, a C.
Эта функция многозначная, её главное значение равно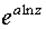 
.
При a=1/n, n N получаем многозначную функцию – корень n-й степени из z:
7. Функции, обратные к тригонометрическим и гиперболическим, являются многозначными и выражаются через логарифмическую.
Поясним сказанное на примере функций а) w= аrcsin z, б) w= аrth z.
a)Имеем по определению
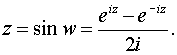
Откуда
(Знаки ± в формуле решения квадратного уравнения можно опустить, если понимать корень как двузначную функцию).
Итак,
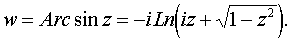
б)По определению w= аrthz Û z= thw. Откуда получаем
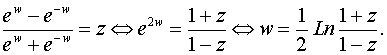
Таким образом,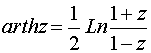 
.
Для остальных обратных тригонометрических функций выполняются формулы:
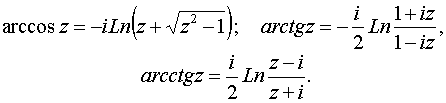
Аналитические функции. Условия Коши-Римана.
Аналитическая функция (действительного переменного) — функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.
|
|
|
Однозначная функция f называется аналитической в точке z0, если сужение функции f на некоторую окрестность z0 является аналитической функцией. Если функция аналитична в точке z0 то она аналитическая в каждой точке некоторой окрестности точки z0.
Аналитическая функция (комплексного переменного) - функция комплексного переменного f(z)=u(z)+iv(z) (где u(z) и v(z) - вещественнозначные функции комплексного переменного, являющиеся, соответственно, вещественной и мнимой частью рассматриваемой функции), для которой в некоторой области A∈C, называемой областью аналитичности, выполняется одно из трех равносильных условий:
1. Для вещественной и мнимой части этой функции в каждой точке z=x+iy∈A выполняются условия Коши - Римана (аналитичность в смысле Коши - Римана);
2. Ряд Тейлора функции в каждой точке z∈A сходится и его сумма равна f(z) (аналитичность в смысле Вейерштрасса);
3. Интеграл ∫Γf(z)dz=0 для любой замкнутой кривой Γ⊂A (аналитичность в смысле Коши)
Условия Коши-Римана, которые также в некоторых источниках называются условиями Даламбера-Эйлера - соотношения, связывающие вещественную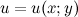 
и мнимую 
части всякой дифференцируемой функции комплексного переменного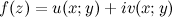 
, где 
.
|
|
|
Для того чтобы функция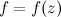 
, которая определена в некоторой области комплексной плоскости 
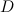, была дифференцируема в точке 
, необходимо и достаточно, чтобы её вещественная и мнимая част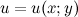и и были дифференцируемы в точке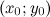 
как функции вещественных переменных 
и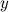 
и в этой точке выполнялись условия Коши-Римана:
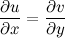
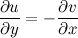
Эти условия впервые появились в работе французского ученого-энциклопедиста, философа, математика и механика Жана Лерона Даламбера (1717 - 1783) в 1752 году. В работе швейцарского, немецкого и российского математика и механика Леонардо Эйлера (1707 - 1783), доложенной Петербургской академии наук в 1777 году, условия получили впервые характер общего признака аналитичности функций. Великий французский математик и механик Огюстен Луи Коши (178 9- 1857) пользовался этими соотношениями для построения теории функций.
Пусть задана действительная часть 
функции комплексной переменной 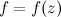. Требуется найти мнимую часть 
этой функции. Найти саму функцию 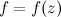, используя некоторое начальное условие.
Алгоритм решения состоит в следующем:
1) Используя условия Коши-Римана, находим мнимую часть .
|
|
|
2) Когда и действительная, и мнимая части функции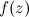 
известны, составляем функцию 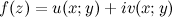. Далее в полученном выражении надо произвести такие преобразования, чтобы выделить переменную или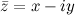 
, то есть "избавиться" от переменных и .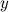
Замечание 1
На практике будут полезны соотношения:
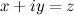
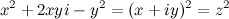
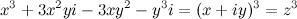
Замечание 2
Поделить на мнимую единицу 
равносильно умножению на 
.
3) В конечном итоге будет получена функция 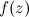, выражение которой содержит только комплексную переменную 
и константы. Используя начальное условие, если оно задано, находим значение константы и окончательно получаем искомую функцию.
Аналогично по известной мнимой части можно найти действительную часть . Алгоритм решения практически идентичен.
Дата добавления: 2018-06-27; просмотров: 635; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!