Принцип сжимающих отображений.
Def Отображение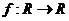 
метрического пространства в себя называется сжимающим, если существует такое число 
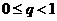, что 
.
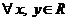
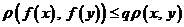При этом точка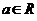 
называется неподвижной точкой отображения 
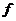, если 
.
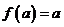Теорема (Принцип сжимающих отображений). Всякое сжимающее отображение в полно метрическом пространстве имеет одну и только одну неподвижную точку.
Неподвижная точка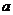 
может быть найдена методом последовательных приближений
, где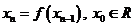 
.
Определение компактного пространства, Критерий компактности Хаусдорфа в метрическом пространстве.
Теорема 1. (Хаусдорфа) Для того, чтобы метрическое пространство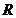 
было компактным необходимо и достаточно, чтобы оно было:
1) вполне ограниченным
2) полным.
Следствие: Компактное пространство 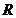сепарабельно [Л.С., с.53].
Укажем на связь между полной ограниченностью и предкомпактностью.
Теорема 2. Для того, чтобы множество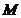 
из полного метрического пространства 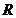было предкомпактным, необходимо и достаточно, чтобы оно было ограничено.
Вполне ограниченное множество, Теорема Арцела-Асколи.
Теорема Арцела-Асколи. Вопрос о компактности множества 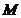из пространства 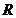- распространенная задача. Теорему 1 из 2.1. применять сложно, поэтому для каждого пространства полезно дать специальные критерии компактности (или предкомпактности) более удобные на практике.
В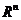 
предкомпактность равносильна ограниченности.
В пространстве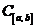 
критерий компактности имеет вид
|
|
|
Теорема Арцела-Асколи. Для того, чтобы множество 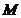непрерывных функций, определенных на отрезке 
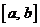было предкомпактно в 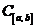, необходимо и достаточно, чтобы оно было:
1) равномерно ограничено
2) равностепенно непрерывно.
Def. Множество 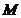функций 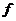равномерно ограничено на 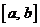, если 
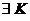, такое, что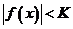 
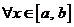, для всех 
.
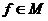Def. Множество 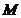функций 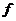равностепенно непрерывно, если 
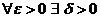, такое, что как только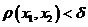 
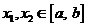сразу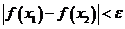 
.
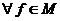Интеграл Лебега, суммируемые функции.
Пусть 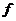некоторая простая функция, принимающая значения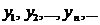 
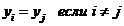и пусть 
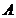некоторое измеримое подмножество 
.
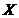Определим интеграл от функции 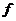по множеству 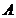равенством
(1) 
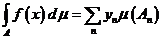, где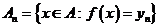 
если ряд справа сходится.
Def Простая функция 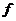называется интегрируемой или суммируемой (по мере 
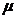) на множестве 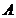, если ряд (1) абсолютно сходится.
Если 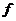интегрируема, то сумма ряда (1) называется интегралом от 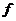по множеству .
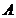Def Функция 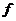называется суммируемой (интегрируемой) на множестве 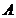, если существует последовательность простых интегрируемых функций 
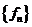, сходящихся равномерно к .
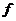Предел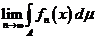 
обозначим 
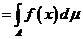и назовем интегралом функции 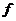по множеству .
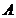Таким образом, построение интеграла Лебега разбивается на два этапа.
Первый: непосредственное определение интеграла как суммы ряда для класса простых суммируемых функций, достаточно простого.
|
|
|
Второй: Распространение определения интеграла на более широкий класс с помощью предельного перехода.
Заметим, что сочетание двух этапов, подобных этим, присутствует при любом построении интеграла.
Дата добавления: 2018-06-27; просмотров: 414; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!