Определение линейного функционала, Примеры.
Def Пусть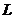 
- линейное нормированное пространство. Числовую функцию 
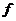, определенную на 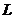называют функционалом 
.
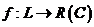Def Функционал называется линейным, если 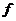обладает свойствами:
1) аддитивности: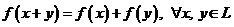 
.
2) Однородности: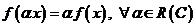 
.
1.1. Примеры линейных функционалов
№ 1. Пусть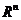 
есть 
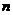-мерное пространство с элементам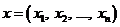и 
и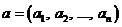 
- произвольный набор из 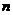фиксированных чисел. Тогда 
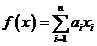- линейный функционал в .
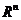№ 2 В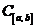 
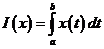
№ 3. В 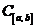более общий случай 
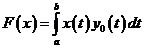, где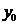 
некоторая фиксированная непрерывная функция на 
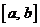. Линейность следует из основных свойств операции интегрирования.
№ 4. В 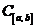рассмотрим другой функционал 
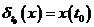, т.е. фиксируем точку 
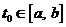и для каждой функции 
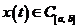функционал равен значению этой функции в данной точке. Этот функционал обычно записывают через 
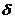-функцию Дирака
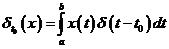, где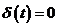 
всюду, кроме 
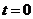, и интеграл от которой равен 1.
№ 5.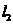 
Пусть 
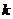- фиксированное
Определение нормы функционала.
Def Нормой линейного непрерывного функционала 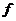называется число 
,
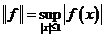Равносильные определения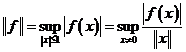 
.
Из последнего определения следует очевидное свойство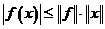 
.
Продолжение функционала, заданного на подпространстве. Теорема Хана-Банаха.
Более сложный случай возникает, если функционал задан на подмножестве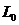 
, не являющимся всюду плотным в .
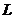Теорема Хана-Банаха.
Пусть 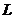- линейное нормированное пространство, 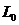- его подпространство. Тогда для любого непрерывного функционала 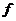, заданного на 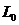, существует такой функционал 
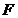, заданный на всем 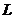, что 1) 
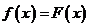, если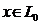 
|
|
|
2) 
.
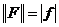4.3. Следствие из теоремы Хана-Банаха.
Следствие 1.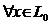 
, 
, 
.
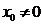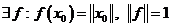Следствие 1 утверждает существование в любом линейном нормированном пространстве линейного непрерывного функционала, не равного тождественно нулю..
Следствие 3. Пусть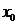 
- фиксированный элемент из 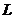. Если 
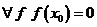, то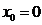 
.
Следствие 4. (Об отделимости элемента и подпространства)
Пусть 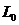- подпространство . 
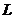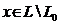и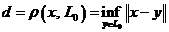 
.
Тогда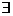 
линейный функционал 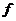, определенный всюду на 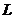и такой, что
1) 
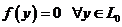
2) 
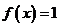
3) 
.
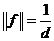Следствие 5 (Критерий замкнутости системы). Для того чтобы система элементов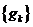 
была замкнутой необходимо и достаточно, чтобы из того, что функционал 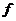обращается в нуль на всех элементах 
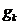следовало, что 
.
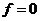Сопряженное пространство.
Пусть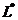 
- множество всех линейных непрерывных функционалов, определенных на 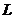. Введем в 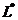операции сложения и умножения на число
; 
.
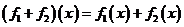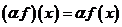Примем за норму элемента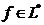 
норму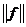 
соответствующего функционала. Поскольку она также удовлетворяет всем аксиомам нормированного пространства, то 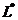- линейное нормированное пространство. Оно называется сопряженным пространством к .
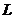Т.к. 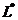линейное нормированное пространство, то можно говорить о пространстве 
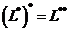, непрерывных линейных функционалов на 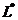, т.е. о втором сопряженном пространстве к .
|
|
|
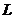Def Те пространства для которых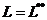 
называются рефлексивными.
В этом случае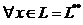 
и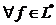 
( 
)
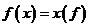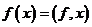Вложение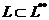 
желательно определять равенством .
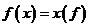Дата добавления: 2018-06-27; просмотров: 2319; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!