Степенные ряды. Теорема Абеля для степенных рядов. Радиус и круг сходимости.
Экзаменационные вопросы
Комплексные числа. Три формы записи, модуль, аргумент, арифметические операции, сопряжение, формула Муавра, извлечение корня.
Комплексное число — это число вида z = x + iy, где x и y — вещественные числа, i — мнимая единица, опре- деляемая следующим образом: i = √ −1 или i2 = −1. Действительное число  называется действительной частью комплексного числа
называется действительной частью комплексного числа 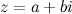 и обозначается
и обозначается 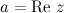 . Действительное число
. Действительное число  называется мнимой частью числа
называется мнимой частью числа 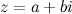 и обозначается
и обозначается 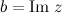 .
.
Запись комплексного числа  в виде
в виде 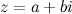 , где
, где  и
и  - действительные числа, называется алгебраической формойкомплексного числа. Например.
- действительные числа, называется алгебраической формойкомплексного числа. Например. 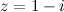
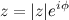
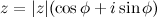 Если
Если 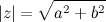 - модуль комплексного числа
- модуль комплексного числа 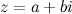 , а
, а 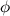 - его аргумент, то тригонометрической формойкомплексного числа
- его аргумент, то тригонометрической формойкомплексного числа  называется выражение
называется выражение
Показательной формой комплексного числа 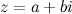 называется выражение
называется выражение
Модуль комплексного числа.Комплексное число также можно изображать радиус-вектором  (рис. 2). Длина радиус-вектора, изображающего комплексное число
(рис. 2). Длина радиус-вектора, изображающего комплексное число 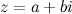 , называется модулем этого комплексного числа.
, называется модулем этого комплексного числа.
Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чиселравны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.
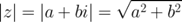 Модуль вычисляется по формуле:
Модуль вычисляется по формуле:
Аргумент комплексного числа.Угол 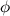 между положительным направлением действительной оси и радиус-вектора
между положительным направлением действительной оси и радиус-вектора  , соответствующим комплексному числу
, соответствующим комплексному числу 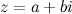 , называется аргументом этого числа и обозначается
, называется аргументом этого числа и обозначается 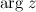 .
.
|
|
|
Аргумент 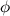 комплексного числа
комплексного числа 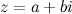 связан с его действительной и мнимой частями соотношениями:
связан с его действительной и мнимой частями соотношениями:
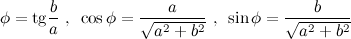
На практике для вычисления аргумента комплексного числа обычно пользуются формулой:
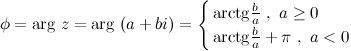
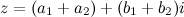 Суммой двух комплексных чисел
Суммой двух комплексных чисел 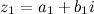 и
и 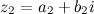 называется комплексное число
называется комплексное число  , которое равно
, которое равно
То есть суммой двух комплексных чисел есть комплексное число, действительная и мнимая части которого есть суммой действительных и мнимых частей чисел-слагаемых соответственно.
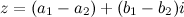 Разностью двух комплексных чисел
Разностью двух комплексных чисел 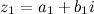 и
и 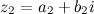 называется комплексное число
называется комплексное число 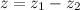 , действительная и мнимая части которого есть разностью действительных и мнимых частей чисел
, действительная и мнимая части которого есть разностью действительных и мнимых частей чисел 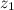 и
и 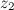 соответственно:
соответственно:
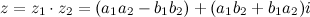 Произведением двух комплексных чисел
Произведением двух комплексных чисел 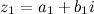 и
и 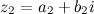 называется комплексное число
называется комплексное число  , равное
, равное
На практике чаще всего комплексные числа перемножают как алгебраические двучлены 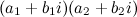 , просто раскрыв скобки, в полученном результате надо учесть, что
, просто раскрыв скобки, в полученном результате надо учесть, что 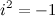 .
.
Если комплексные числа 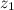 и
и 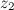 заданы в геометрической форме:
заданы в геометрической форме: 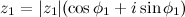 ,
, 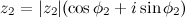 , то произведением этих чисел есть число
, то произведением этих чисел есть число
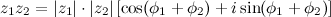
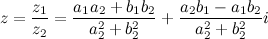 Частным двух комплексных чисел
Частным двух комплексных чисел 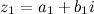 и
и 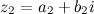 называется число
называется число  , которое задается соотношением:
, которое задается соотношением:
На практике деление комплексных чисел проводят по следующей схеме:
|
|
|
1. сначала делимое и делитель умножают на число, комплексно сопряженное делителю, после чего делитель становится действительным числом;
2. в числителе умножают два комплексных числа;
3. полученную дробь почленно делят.
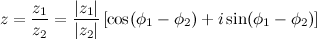 Если надо поделить комплексные числа
Если надо поделить комплексные числа 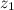 и
и 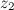 в геометрической форме:
в геометрической форме: 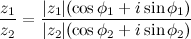 , то искомое число
, то искомое число
То есть модуль частного двух комплексных чисел равен частному модулей, а аргумент - разности аргументов делимого и делителя.
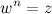
Корнем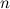 -ой степени из комплексного числа
-ой степени из комплексного числа  называется такое комплексное число
называется такое комплексное число 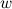 ,
, 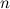 -я степень которого равна
-я степень которого равна  , то есть Корень
, то есть Корень 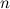 -ой степени из комплексного числа
-ой степени из комплексного числа  обозначается символом
обозначается символом 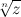 и на множестве комплексных чисел имеет ровно
и на множестве комплексных чисел имеет ровно 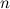 значений.
значений.
Если комплексное число  задано в тригонометрической форме:
задано в тригонометрической форме: 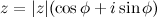 , то все значения корня
, то все значения корня 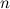 -ой степени вычисляются по формуле Муавра (Абрахам де Муавр (1667 - 1754) - английский математик):
-ой степени вычисляются по формуле Муавра (Абрахам де Муавр (1667 - 1754) - английский математик):
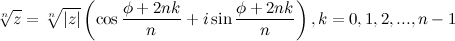
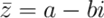 Геометрически все значения корня лежат на окружности радиуса
Геометрически все значения корня лежат на окружности радиуса 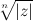 с центром в начале координат и образуют правильный
с центром в начале координат и образуют правильный 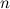 -угольник.
-угольник.
Если 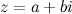 , то число
, то число 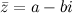 называется комплексным сопряженным к числу
называется комплексным сопряженным к числу  .
.
То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.
Например. Комплексно сопряженным к числу 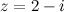 есть число
есть число 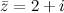 .
.
|
|
|
На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси. Свойства комплексно сопряженных чисел:
1) Если 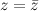 , то можно сделать вывод, что рассматриваемое число
, то можно сделать вывод, что рассматриваемое число  является действительным.
является действительным.
Например. 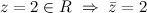 и
и 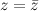
2) Для любого комплексного числа  сумма
сумма 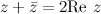 - действительное число.
- действительное число.
Например. Пусть 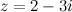 , тогда
, тогда 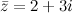 , а тогда
, а тогда
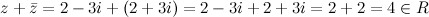
3) Для произвольного комплексного числа 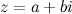 произведение
произведение 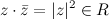 .
.
Например. Пусть 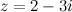 , комплексно сопряженное к нему число
, комплексно сопряженное к нему число 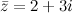 , тогда произведение
, тогда произведение
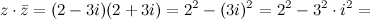
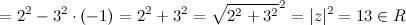
4) Модули комплексно сопряженных чисел равны: 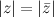 , а аргументы отличаются знаком
, а аргументы отличаются знаком
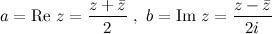 5)
5)  6)
6)  7)
7) 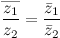 8)
8) 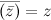 9) Если
9) Если 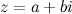 и
и 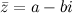 - комплексно сопряженные числа, то
- комплексно сопряженные числа, то
Степенные ряды. Теорема Абеля для степенных рядов. Радиус и круг сходимости.





Дата добавления: 2018-06-27; просмотров: 398; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
