Теорема Нернста. Третье начало термодинамики.
Теорема Нернста: При стремлении температуры тела к 0, его энтропия также стремится к 0 независимо от значений внешних параметров:
.
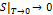Энтропия – это физ. величина, используемая для описания термодинамической системы. Энтропия является функцией состояния, т.е. любому состоянию можно сопоставить вполне определенное (с точностью до константы) значение энтропии.
В термодинамике теорема Нернста выступает как опытный факт, не вытекающий из первого и второго принципа. На этом основании, а также с учетом большой практической значимости теорема Нернста выступает как третий принцип термодинамики.
Теорема Нернста применима только к телам, для которых состояния при абсолютном 0 температуры являются состояниями полного внутреннего равновесия. С квантовомеханической точки зрения такая ситуация возможна лишь в том случае, когда основное состояние тела (состояние м наименьшей энергией) невырождено. Практически применимость теоремы сводится к 3-м случаям:
1. Кристаллы с полной упорядоченностью внутренней структуры
2. Жидкий гелий II – изотоп гелия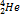 
3. Некоторые невырожденные газы элементарных частиц
Аморфное состояние не является состоянием полного внутреннего равновесия ТТ. Поэтому, теорема Нернста неприменима к аморфным телам.
Рассмотрим наиболее важные следствия из теоремы.
Теорема Нернста привносит естественное начало отсчета энтропии. В общем случае внутренняя энергия тела и выражаемая через нее теплоемкость зависят от объема и температуры, и можно записать:
|
|
|
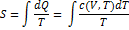
Известно, что при интегрировании функции двух переменных вместо произвольной константы интегрирования появляется произвольная функция по переменной, по которой не производилось интегрирование:
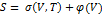
Здесь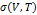 
– известная функция, результат взятия интегрирования, а 
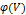– произвольная функция. Следовательно, в общем случае энтропия определяется с точностью до произвольной функции объема. Это делает невозможным определение не только самой энтропии, но и изменений при переходах между состояниями, поскольку 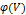не приводится к 0. Выход из данной ситуации дает теорема Нернста.
,
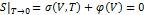
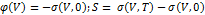И энтропия становится определенной.
Из того факта, что стремление энтропии к 0 не зависит от внешних параметров, следует, что существует множество состояний с нулевой энтропией, различающихся значениями внешних параметров. Эти состояния лежат на нулевой адиабате – самой нижней из семейства адиабат тела. Поскольку S=0 только при T=0, нулевая адиабата одновременно является нулевой изотермой.
При движении вдоль нулевой адиабаты происходит сжатие или растяжение кристалла действием внешних сил. При этом совершается работа, но температура кристалла остается равной 0. Отсюда следует, что совершаемая на нулевой адиабате работа направлена на изменение нетепловых форм внутренней энергии, т.е. форм, не зависящих от температуры и не исчезающих при абсолютном 0. В кристалле такими формами являются энергия нулевых колебаний атомов и энергия межатомных взаимодействий, которая с макроскопической точки зрения предстает как упругая энергия кристалла.
|
|
|
Очень важный вывод из теоремы Нернста состоит в том, что теплоемкость кристаллов (с) стремится к 0 при стремлении к 0 абсолютной температуры.
Еще один вывод состоит в том, что к абсолютному 0 температуры можно подойти как угодно близко, но точно достигнуть 0 невозможно. Формально это обусловлено тем, что стремящаяся к 0 теплоемкость вблизи абсолютного 0 становится исчезающе малой. Это означает, что в непосредственной близости к абсолютному 0 кристалл практически перестаёт отдавать внутреннюю энергию в форме теплоты. Физически это объясняется тем, что кристалл переходит в основное квантовое состояние, т.е. в состояние с наименьшей возможной энегрией.
25. Корпускулярно – волновой дуализм свойств вещества. Волны де Бройля.Соотношение неопределенностей Гейзенберга.
|
|
|
Гипотеза де Бройля: установленный ранее для квантов света – фотонов корпускулярно-волновой дуализм присущ и всем частицам вещества – электронам, протонам, атомам и т.д., причем количественные соотношения между волнами и корпускулярными характеристиками свободных частиц те же, что и для фотонов. Таким образом, если частица имеет энергию W и импульс, модуль которой равен p, то соответствующие волновые характеристики частицы – частота ω и длина волны λ связаны с корпускулярными соотношениями:
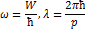
Волны, ассоциированные со свободно движущимися частицами, получили название де Бройля. Для частиц не очень высокой энергии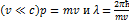 
, где m и v – масса и скорость частицы. Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и ее скорость.
Движение микрочастиц в квантовой механике описывается вероятностным образом, естественно ожидать, что в заданном квантовом состоянии некоторые физические величины, характеризующие микрочастицу, являются случайными – т.е. не имеют строго определенных значений. При этом оказывается, что неопределенности некоторых физических величин не являются независимыми, а связаны между собой некоторыми соотношениями.
|
|
|
Соотношения неопределённостей Гейзенберга для координат и проекций импульса микрочастицы:
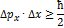
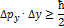
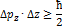
Под неопределенностями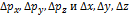 
понимаются среднеквадратичные отклонения проекций импульса и проекций координат от их средних значений, т.е. дисперсии этих СВ.
Физическое содержание этих соотношений состоит в том, что в противоположность классической механике в квантовой механике не существует такого состояния, в котором координата и соответствующая проекция импульса частицы не имеют одновременно точные значения.
Соотношения такого вида имеют место также в частности для неопределенности полной энергии ΔW микрочастицы в некотором квантовом состоянии и временем Δt ее пребывания в этом состоянии:
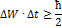
В связи с соотношениями неопределённостей важно отметить, что некоторые величины могут быть одновременно точно определены. Совокупность таких величин называют полным набором одновременно измеримых величин.
26.
Дата добавления: 2018-06-27; просмотров: 446; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!