Энтропия - это функция состояния системы, связанная со статистическим весом формулой
S = k ln W.
С этой точки зрения энтропия выступает как мера беспорядочности, хаотичности состояния.
Связь между S и W позволяет несколько иначе сформулировать второе начало термодинамики: наиболее вероятным изменением энтропии является ее возрастание.
Энтропия замкнутой системы максимальна при достижении системой равновесного состояния.
Статистическое равновесие — состояние замкнутой статистической системы, в которомсредние значения всех физических величин, характеризующих состояние, не зависят от времени.
Физический смысл и статистический характер в21)Физический смысл и статистический характер второго начала термодинамики.
Второе начало термодинамики, как и первое, может быть сформулировано несколькими способами. В наиболее очевидной формулировке второе начало гласит, что невозможен самопрозвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Более строго, невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому.
Второе начала может быть также сформулировано следующим образом: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращение этого тепла полностью в работу.
Статистический характер второго закона термодинамики приводит к заключению, что увеличение энтропии в самопроизвольных процессах указывает на наиболее вероятныепути развития процессов в изолированной системе. Невозможность процесса следует понимать лишь как его малую вероятность по сравнению с обратным. Поэтому второй закон термодинамики в отличие от первого нужно рассматривать как закон вероятноститорого начала термодинамики
|
|
|
Распределение максвелла. средние и наивероятнейший скорости молекул
Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.
Нельзя ставить вопрос: сколько молекул обладает определенной скоростью. Дело в том, что, хоть число молекул очень велико в любом даже малом объеме, но количество значений скорости сколь угодно велико (как чисел в последовательном ряде), и может случиться, что ни одна молекула не обладает заданной скоростью.
|
|
|
 Рис. 3.3
|
Задачу о распределении молекул по скоростям следует сформулировать следующим образом. Пусть в единице объема nмолекул. Какая доля молекул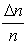 
имеет скорости от v1 до v1 + Δv? Это статистическая задача.
Основываясь на опыте Штерна, можно ожидать, что наибольшее число молекул будут иметь какую-то среднюю скорость, а доля быстрых и медленных молекул не очень велика. Необходимые измерения показали, что доля молекул 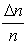, отнесенная к интервалу скорости Δv, т.е. 
, имеет вид, показанный на рис. 3.3. Максвелл в 1859 г.теоретически на основании теории вероятности определил эту функцию. С тех пор она называется функцией распределения молекул по скоростям или законом Максвелла.
Дата добавления: 2018-06-27; просмотров: 280; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!