Аналитически она выражается формулой
|
где m – масса молекулы, k – постоянная Больцмана.
Установление этой зависимости позволило определить кроме уже известной среднеквадратичной скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема.
Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой
|
Или
 .
|
Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул. Она рассчитывается по формуле:
 .
|
Распределение Больцмана для идеального газа во внешнем потенциальном поле. Барометрическая
Формула.
Рассмотрим идеальный газ во внешнем потенциальном поле. Распределение Больцмана молекул идеального газа по потенциальным энергиям, а стало быть, и по координатам во внешнем потенциальном поле запишется в виде:
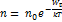(1)
Здесь n = n(x, y, z) – плотность молекул в окрестности точки поля, в которой их потенциальная энергия равна 
.
Как известно, в состоянии статистического равновесия при отсутствии внешнего поля молекулы газа в среднем равномерно распределены по элементам объема сосуда, в котором находится газ. Из распределения Больцмана следует, что эта равномерность нарушается при включении внешнего поля. Плотность молекул при этом возрастает в элементах, где их потенциальная энергия молекул меньше. Физическая причина такого перераспределения состоит в следующем. При включении поля в газе действуют две противоположные тенденции. Тепловое движение молекул в силу своего хаотического характера стремится распределить молекулы равномерно по объему газа. С другой стороны, включенное поле действует на молекулы с силой, выражаемой известным соотношением:
|
|
|
,
из которого следует, что сила поля всегда действует в направлении наиболее быстрого убывания потенциальной энергии. Поэтому поле стремится переместить молекулы газа в область с наименьшим значением потенциальной энергии. Поскольку обе тенденции действуют одновременно, в ходе межмолекулярных столкновений устанавливается некоторое компромиссное состояние, которое и выражается распределением Больцмана.
Рассмотрим частный случай распределение Больцмана, когда во внешним полем, в котором находится газ, являются гравитационное поле Земли и когда потенциальная энергия молекулы выражается как 
. Здесь h – это высота над уровнем, на котором потенциальная энергия принята равной 0. Распределение (1) принимает вид, называемый барометрической формулой:
|
|
|
(2),
где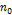 
– плотность молекул на нулевом уровне h=0, а n – плотность на высоте h. Умножив обе части (2) на kT и учитывая, что nkT = P – давление газа, барометрическую формулу можно записать еще в виде:
.
Барометрическая формула часто применяется для расчета зависимости плотности и давления атмосферы от высоты над поверхностью Земли. Но это можно делать только для не очень больших высот, не превышающих несколько км. Дело в том, что барометрическая формула предполагает изотермичность газа T = const, в то время, как температура земной атмосферы убывает с ростом высоты.
В связи применением барометрической формулы к атмосфере вводится понятие о характеристической высоте. Характеристической высотой данного газа является высота H, на которой давление этого газа в e раз меньше, чем на поверхности Земли, где e ≈ 2,7 – основание натуральных логарифмов. Очевидно
.
Здесь R – газовая постоянная, 
– молекулярная масса газа.
Дата добавления: 2018-06-27; просмотров: 286; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!