Билет Статистическая физика. Вероятность. Среднее значение. Предмет статистической физики. Статистические закономерности.
Статистическая физика изучает системы, состоящие из очень большого числа частиц: молекул, атомов, ионов и др. Основная задача статистической физики — изучение связи макроскопических свойств изучаемых систем со свойствами и законами движения микрочастиц, составляющих данную систему.
Билет Макро - и микросостояния. Статистический ансамбль. Средние значения макроскопических характеристик.
Состояние макроскопического тела может быть задано с помощью параметров состояния P,V,T
Состояние макротела, охарактеризованное настолько подробно, что оказываются заданными состояния всех образующих тело молекул, называется Микросостоянием
Микросостояние – то, как организованно макросостояние.
Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весомилитермодинамической вероятностью макросостояния.
Сосуд с заключенными в нем частицами называется статистической системой.
Совокупность одинаковых статистических систем называется статистическим ансамблем.
Микроканонический ансамбль состоит из одинаковых изолированных систем с одинаковой энергией. Кроме микроканонических ансамблей в статистической физике рассматриваются также канонические и некоторые другие ансамбли.
Одно и тоже макроскопическое состояние осуществляется в большом числе систем ансамбля, находящихся в различных микроскопических состояниях. Следовательно, данное макросостояние характеризуется большим числом микросостояний.
|
|
|
Эргодическая гипотеза. Микроканонические распределения. Энтропия в статистической физике. Статистическое равновесие
ЭРГОДИЧЕСКАЯ ГИПОТЕЗА в с т а т и с т и ч е с к о й ф и з и к е - предположение, что с р е д н и е п о в р е м е н и значения физ. величин, характеризующих систему, равны их с р е д н и м с т а т и с т и ч е с к и м. Предложена Л. Больцманом в 1887 для обоснования статистической физики.
В классич. статистич. физике равновесных систем Э. г. основана на предположении, что средние по времени от фазовых переменных (ф-ций, зависящих от координат q и импульсов р всех частиц замкнутой и энергетически изолированной системы), взятые вдоль траектории движения системы в фазовом пространстве, равны средним статистическим по равномерному распределению фазовых точек в тонком (в пределе - бесконечно тонком) слое вблизи поверхности постоянной энергии. В квантовой статистич. физике Э. г. есть предположение, что все энергетич. состояния в тонком слое вблизи поверхности постоянной энергии равновероятны. Э. г. эквивалентна, т. о., предположению, что замкнутая система (как классическая, так и квантовая) может быть описана микроканоническим распределением Гиббса. Напр., для классических замкнутых систем из N частиц с Гамильтона функцией HN (p, q)в объёме V почти всегда существуют средние по времени от функции фазовых переменных F(p(t), q(t))
|
|
|
где эволюция р (t), q (t)во времени определяется из решения ур-ний Гамильтона. Согласно Э. г.,
где dГN=dpdq/N!h3N - элемент фазового объёма в безразмерных переменных; fм.к.(р, q)-микроканонич. распределение, имеющее вид
(интегрирование проводится по всем "микроскопическим" состояниям системы, энергия к-рых лежит в слое энергии шириной
); 
-статистический вес, связанный с энтропией S соотношением S=k ln W.
МИКРОКАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ГИББСА - равновесное распределение вероятностей для статистич. ансамбля систем с заданной полной энергией 
при пост, объёме V и пост, полном числе частиц N, соответствует микроканоническому ансамблю Ги6бса. Установлено Дж. У. Гиббсом (J. W. Gibbs) в 1901 для случая классич. статистики как один из осн. законов статистической физики.
В классич. статистич. механике ф-ция распределения /(р, q)зависит от координат и импульсов р, q всех частиц через Гамильтона функцию H (р, q), к-рая является интегралом движения системы. Согласно M. р. Г., все микроскопич. состояния в узком слое энергии 
равновероятны, а вероятности др. состояний равны нулю, т. е.
|
|
|
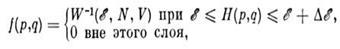
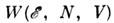- статистич. вес, определяемый из условия нормировки (суммарная вероятность пребывания системы во всех состояниях равна 1). Следовательно,
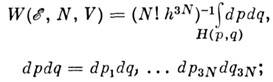
эта величина слабо зависит от ширины слоя 
при больших N этой зависимостью можно пренебречь. В случае классич. механики можно перейти к пределу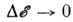 
и записать M. р. Г. в виде
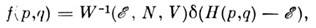
- дельта-функция Дирака. Статистич. вес связан с энтропией 
соотношением
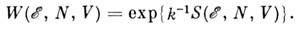
Дата добавления: 2018-06-27; просмотров: 382; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!