Волновые процессы. Волновое уравнение. Монохроматическая волна. Дисперсия волн. Фазовая и групповая скорости. Плотность потока, и поток энергии. Вектор Умова.
Общие представления о колебательных и волновых процессах. Колебания. Гармонические и негармонические колебания. Сложение гармонических колебаний.
Любой физический процесс отличающийся некоторой степенью повторяемости называется колебанием. Гармоническим колебанием называются колебания, время повторений которого постоянна, другие колебания называются ангармоническими или негармоническими. Фурье в свое время доказал, что любое негармоническое колебание можно разложить в ряд гармонических колебаний:
Гармонический осциллятор. Движение частицы вблизи устойчивого состояния равновесия. Примеры гармонического осциллятора. Свободные и вынужденные колебания.
Гармоническое колебание:
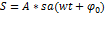, где A-амплитуда колебаний; w= 
, где T- период; 
, 
циклическая частота ( 
Система, где происходит гармонические колебания называют гармоническим осциллятором. В гармоническом осцилляторе должна быть причина 
, возвращающая систему в состояние устойчивого равновесия. Эта причина должна быть прямо пропорциональна отклонению системы от состояния равновесия. Данную причину называют квазиупругой.
Состояние устойчивого равновесия называется состояние, при котором система 
принимает минимальное значение.
Отчасти для некоторых систем 
Примеры гармонических осцилляторов:
1. Математический маятник
2. Физический маятник
3. Пружинный маятник
|
|
|
Примеры гармонических осцилляторов. Математический, пружинный и физический маятники. Колебательный контур.
1. Математический маятник:
t=0, s=A, v=0, φ→0, s=x, 
, 
φ→ 
=> 
, 
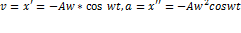
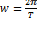
2. Физический маятник
, E-угловое ускорение
E= 
, E= 
; M=r*mg*sinφ 
φ->0=>sinφ=φ
s=A*coswt, -rmgφ=I 
φ=A*coswt -rmgφ=- 
φI
=- w= 
r= 
– расстояние от оси до ц.м.
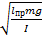w= 
, w= 
T=2π 
Для мат. Точки:
I=m 
, 
3.Пружинный маятник
ma=kx, a= 
, a=-x 
, w= 
T= 
4. Колебательный контур
Конденсатор
, C=E 
, 
L-индуктивность
, 
, E= 
, I= 
( 
= 
, I’= 
( 
L 
, w= 
q= 
, T=2π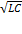 
, 
Цепь переменного тока. Векторная диаграмма. Импеданс. Резонанс.
Электрический ток, возникающий под действием э. д. с, которая изменяется по синусоидальному закону, называют переменным. По существу, переменный ток — это вынужденные колебания тока в электрических цепях.
Амплитудой переменного тока называется наибольшее значение, положительное или отрицательное, принимаемое переменным током.
Периодом называется время, в течение которого происходит полное колебание тока в проводнике.
Частота - величина, обратная периоду.
Фазой называется угол 
или 
, стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
|
|
|
, 
, R=ρ 
Закон Ома для участка цепей: IR=U, U= 
Закон Ома для замкнутых цепей:E=I(R+r)
Для последовательных:
Для параллельных:
Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений, либо их амплитудных величин.
Векторная диаграмма
При расчете электрических цепей переменного тока пользуются весьма простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов. Обоснование векторной диаграммы
Предположим, что ток задан уравнением
i = Imsin(ωt +Ψ)
Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем векторIm, длина которого в определённом масштабе Mi выражает амплитуду тока Im:
Im = Im/Mi
Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе Ψ (рис. 12.10).
Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени:i0 = ImsinΨ.
|
|
|
Представим себе, что вектор Im вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом ωt +Ψ ,
Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора Im на вертикальную ось в этот момент времени.
Следующая статья сложение и вычитания векторов векторной диаграммы. Например, для t = t1
i1 = Imsin(ωt1 +Ψ)
в общем случае
i = Imsin(ωt +Ψ)
Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж в начальном положении.
Импеданс
Импедансом называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени: если время t в выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.
Для катушки индуктивности импеданс равен 
.
Здесь:
- j — мнимая единица;
- ω — циклическая частота;
- U(ω), I(ω) — амплитуды напряжения и тока гармонического сигнала на частоте ω;
- ϕu(ω), ϕi(ω) — фазы напряжения и тока гармонического сигнала на частоте ω;
|
|
|
Резонанс
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того, как они соединены различают резонанс напряженийирезонанс токов.
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений возникает в последовательной RLC-цепи.
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжениеисточника, что опасно для цепи.
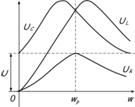
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
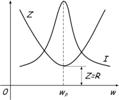
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
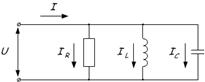
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.
Выразим резонансную частоту
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к авариям.
Волновые процессы. Волновое уравнение. Монохроматическая волна. Дисперсия волн. Фазовая и групповая скорости. Плотность потока, и поток энергии. Вектор Умова.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия без переноса самого вещества.
Типы волн: волны на поверхности жидкости, упругие и электромагнитные волны.
Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике. В общем случае волна, распространяющаяся в пространстве, описывается уравнением: 
, где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны.
Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид: 
, где 
– волновое число, 
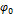– начальная фаза, 
– амплитуда колебаний (const).
Плоская бегущая монохроматическая волна является частным случаем сферической волны. 
; 
, где r – радиус вектор, 
, 
, 
– нормаль к поверхности.
Дисперсия волн — зависимость фазовой скорости гармонических волн в среде от частоты их колебаний; наблюдается для волн любой природы. Дисперсия волн определяется физическими свойствами той среды, в которой распространяются волны. Наличие дисперсии волн приводит к искажению формы сигналов при распространении их в среде. Это объясняется тем, что гармонические волны разных частот, на которые может быть разложен сигнал, распространяются с различной скоростью. Дисперсия света наблюдается в виде разложения белого света в спектр, например, при прохождении света сквозь стеклянную призму.
Фазовая скорость — скорость перемещения точки, обладающей постоянной фазой колебательного движения в пространстве, вдоль заданного направления.
Групповая скорость — это величина, характеризующая скорость распространения «группы волн» — т.е. более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром). Обычно интерпретируется как скорость перемещения максимума амплитудной огибающей квазимонохроматического волнового пакета (или цуга волн).
Поток энергии — это количество энергии, переносимое через некоторую произвольную площадку в единицу времени. Вектор плотности потока энергии: 
, где 
- энергия, переносимая за время 
через площадку 
, перпендикулярную к направлению переноса энергии. Направление вектора 
совпадает с направлением распространения энергии волны.
Вектор Умова-Пойтинга - это вектор, который показывает, куда и сколько энергии переносит электромагнитная волна. Выражается по формуле: 
, где 
- плотность энергии, 
- фазовая скорость волны, направление совпадает с направлением распространения волны.
Дата добавления: 2018-06-27; просмотров: 801; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!