ПРЕДМЕТ МАТЕМАТИКИ В ЕЕ ДИАЛОГИЧЕСКОМ ПОЗНАНИИ В СРЕДНЕЙ ШКОЛЕ
Крушкина А.Н., Буйченок Р.А.,
студентки 5 курса УО «ВГУ им. П.М. Машерова», г. Витебск, Республика Беларусь
Научный руководитель – Семенов Е.Е., профессор
Под предметом математики будем понимать логически мыслимые формы (ЛМФ) и логически мыслимые отношения (ЛМО) [1, с. 3]. Раскроем понятия ЛМФ и ЛМО, их особенности в алгебре и геометрии.
Пример 1. Рассмотрим произвольную трапецию ABCD.
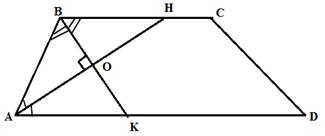
Предложенный рисунок представляет материалозованность этого понятия. В нем наглядно отражены первичные свойства этой ЛМФ.
Трапеция – это четырехугольник, две противолежащие стороны параллельны, а две другие стороны не параллельны. Таким образом, в этой материализации отражаем свойство этой фигуры. Опираясь на эти первичные свойства, мы выявляем новые ЛМО.
Вводим понятие оснований трапеции и боковых сторон трапеции, диагоналей трапеции. Логическим путем выявляем другие ЛМФ, являющиеся следствиями первичных свойств. Свойства, логически вытекающие из первичных, образуют производное содержание понятия трапеции.
Среди свойств, входящих в производное содержание понятия, можно показать следующие:
· сумма прилежащих углов к боковой стороне равна 1800.
· биссектрисы двух углов, прилежащих к боковой стороне трапеции, пересекаются под прямым углом.
Выявление этих свойств означает выявление ЛМО, которые не указаны в определении.
Познание математики состоит в конструировании ЛМФ и выявлении в них ЛМО.
|
|
|
Понятие ЛМФ отличается от понятия фигуры в геометрии. Фигура – это любое множество точек. Если не указаны ЛМО между этими точками, то ее нельзя считать ЛМФ. На основе полученных ЛМФ можем получать новые ЛМФ и выражать в них ЛМО. Если отражаем не математические ситуации на математическом языке, то мы их представляем в материализованном виде, но не в материальном и указываем некоторые свойства, которые отражены в этой теперь уже материализованной ситуации. И, используя имеющиеся ЛМФ, выявляя для них ЛМО, мы можем использовать их как приложение к реальной действительности.
Поскольку теорию математического моделирования можно рассматривать как логическое конструирование фактов, связанных между собой, то и конструирование логических форм можно рассматривать как разновидность математического моделирования.
Аналогичная материализованность в алгебре осуществляется через язык символики. К нему можно отнести буквенные обозначения (греческий и латинский алфавиты) и другие символические знаки. Например, в геометрии вводятся следующие обозначения:
|| 
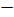параллельные прямые,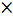 
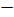пересекающиеся прямые,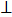 
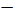перпендикулярные прямые,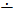 
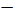скрещивающиеся прямые.
|
|
|
Пример 2. Пусть имеем переменную величину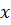 
, которая может принимать любое значение из множества действительных чисел. Пусть другие две переменные величины 
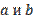принимают любые значения из множества действительных чисел, но считаются заданными. Пусть они связаны следующим образом: 
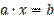. Ставим задачу: необходимо найти такие значения 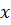, при которых равенство 
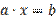, при заданных значениях 
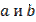обращается в верное числовое равенство. Такие значения 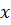будем называть корнями. Решить уравнение, значит найти все его корни или доказать, что их нет.
Мы получили ЛМФ, которая называется уравнением с неизвестной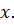 
Итак, имеем уравнение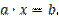 
Осуществляем поиск корней уравнения (этой ЛМФ).
I. Если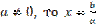 
(воспользовались теоремой о равносильности уравнений).
II. Если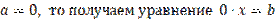 
. Имеем два случая.
a)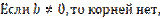 
b)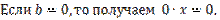 
Корнем уравнения является всякое действительное число.
Для того чтобы раскрыть понятие диалогического познания, раскроем понятие диалога. Под диалогом будем понимать:
ДИА- (гр. dia = через) — префикс, обозначающий проникновение, разделение, взаимосвязь, усиление, завершённость.
ЛОГ (гр. logos— слово, понятие; учение, мысль) — вторая составная часть сложных слов, соответствующая понятиям «тот, кто занимается наукой», «слово», «речь» [2, 3, с. 3].
|
|
|
Познание математики будет продуктивным, если в процессе этого познания внимание акцентируется на понятии предмета математики, а самопознание осуществляется диалогически – содержит в себе проникновение через слово, понятие, учение, мысль.
Литература:
1. Семенов Е.Е. Методология диалогического познания математики // Матэматыка: праблема выкладання. – 2009. – №1. – С. 3—6.
2. Семенов Е. Е. Методология диалогического познания математики // Матэматыка: праблема выкладання. – 2010. – №3. – С. 3—13.
3. Семенов Е. Е. Методология диалогического познания математики // Матэматыка: праблема выкладання. – 2011. – №4. – С. 3—12.
Дата добавления: 2018-05-09; просмотров: 222; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!