Взаимодействия заряженных частиц с веществом.

⇐ ПредыдущаяСтр 10 из 39Следующая ⇒

Прохождение заряженных частиц в веществе существенно отличается от рассмотренного выше прохождения нейтральных частиц. Для нейтральных частиц характерны редкие столкновения и большие пробеги без столкновений; для электронов, например, наоборот, из-за длинно действующих кулоновских сил характерны частые взаимодействия. Так, нейтрон с энергией 0,5 МэВ в процессе замедления до энергии 0,0625 МэВ в алюминии должен испытать около 30 столкновений, фотону для этого потребуется немногим более 10, а электрону необходимо испытать 10⁵ столкновений.

Взаимодействие заряженных частиц с веществом зависит как от характеристик вещества (плотность, атомный номер, ионизационный потенциал), так и от их типа, заряда, массы и энергии частицы. Быстрые заряженные частицы взаимодействуют с электронами и ядрами атомов. Столкновения частиц с ядрами очень редки, так как ядро занимает относительно малый объем в атоме, поэтому они мало влияют на торможение частиц веществом. В результате взаимодействия с быстрой заряженной частицей электрон атома получает дополнительную энергию и переходит на один из удаленных от ядра энергетических уровней или совсем покидает атом. В первом случае происходит возбуждение, во втором – ионизация атома. При прохождении вблизи атомного ядра быстрая частица испытывает торможение в его электрическом поле, что сопровождается испусканием квантов тормозного излучения.

Взаимодействия тяжелых заряженных частиц с веществом.

Упругое рассеяние.

Взаимодействие заряженной частицы с кулоновским полем приводит к рассеянию частицы, которое можно рассматривать как столкновение частицы с целым атомом. Если при этом атом не возбуждается и не ионизируется, то столкновение будет упругим.

Если масса налетающей частицы мала по сравнению с массой ядра, то, пренебрегая передачей энергии атому отдачи и рассматривая ядро как точечный заряд, дифференциальное микроскопическое поперечное сечение упругого рассеяния описывается формулой Резерфорда:

dσ_el (E^/, μ_s)/d μ_s =πZ_a² Z²e⁴/2E^/2Sin⁴(θ_s/2) (3.81),

в которой: Ze, Е^/ - заряд и кинетическая энергия налетающей частицы, Z_ае – заряд ядра, θ_s –угол рассеяния, отсчитываемый от первоначального направления движения частицы, μ_s=Cos θ_s.

Из приведенной формулы видно, что угловое распределение рассеянных частиц имеет сильную анизотропию. Например, для электронов отклонение на угол θ_s =1⁰в 10⁹ раз более вероятно, чем на θ_s =120⁰.

Формула (3.81) приближенная и не учитывает волновые свойства частиц. Квантовомеханическое рассмотрение в приближении Борна с учетом спинов и в предположении малости возмущения падающей плоской волны рассеивающим атомом привело к введению поправки Мотта, а учет экранирования ядерного потенциала атомными электронами проводится поправкой на экранирование Мольера. Указанные поправки, особенно заметные для легких частиц, описываются ниже при рассмотрении взаимодействия электронов с веществом.

Вычислив, исходя из законов сохранения энергии и импульса при упругом рассеянии, потерю энергии частицы ΔЕ(μ_s) при рассеянии на угол θ_s , умножив ее на число упругих столкновений с ядрами среды, находящимися в единице массы, и проинтегрировав по всем углам рассеяния θ_s, можно определить средние потери энергии частицы в массовых единицах в результате упругих рассеяний:

(-dЕ/dx)_el= 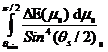= х

х[|lnSin(θ_min/2)| + (A²- MA - M²)/2(M+A)² (3.82).

В формуле (3.82): А – атомная масса ядер среды, N_a - число Авагадро, θ_min – минимальный угол рассеяния, определяемый эффектом экранирования заряда ядра электронной оболочкой, М – масса частицы.

Неупругое рассеяние

В предположении, что масса тяжелой частицы много больше массы электрона (M>>m), взаимодействие ее с электроном приводит к тому, что последний получает импульс в направлении, перпендикулярном к направлению полета частицы, а потеря энергии частицы равна кинетической энергии электрона. В результате произойдет возбуждение атомов мишени и их ионизация (см. § 1.3). Энергетические потери заряженной частицы в неупругих (возбуждение и ионизация) и упругих столкновениях с атомами принято относить к ионизационным потерям. На создание одной пары ионов в веществе все заряженные частицы тратят в среднем одинаковую энергию, из которой одна половина идет на ионизацию, а другая - на возбуждение и на упругие столкновения с молекулами. Например, заряженные частицы расходуют на образование одной ионной пары в воздухе энергию, равную примерно 34 эВ. Из этой энергии на ионизацию идет около 15 эВ, а остальные 19 эВ - на возбуждение и упругие столкновения.

Следует отметить, что в потерях энергии заряженной частицы доминирующую роль играют потери на ионизацию и возбуждение, вклад потерь при упругом рассеянии для тяжелых частиц пренебрежимо мал, он более заметен для электронов.

Если частица имеет энергию большую, чем энергия связи электрона в атоме, массовые ионизационные потери энергии для тяжелых заряженных частиц описываются формулой Бете-Блоха:

(-dЕ/dx)_ион= [ln (3.83),

где mс² – масса покоя электрона; с- скорость света; v - скорость частицы; β=v/c; I – средний ионизационный потенциал атомов вещества среды, через которую проходит частица (I =13,5*Z_a, ,эB), n – число электронов в единице массы, Z –заряд ионизирующей частицы.

Чаще эта формула записывается в виде:

( - dЕ / dx)_ион = 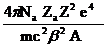[ln 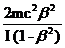- β²] (3.84),

где дополнительно к обозначениям (3.83): N_a – число Авагадро, Z_a и А – атомный номер и атомная масса среды, в которой распространяется частица. Из приведенных зависимостей ионизационных потерь от параметров частицы и свойств среды следует, что массовые потери энергии заряженной частицы на ионизацию пропорциональны квадрату заряда частицы Z, концентрации электронов в среде и не зависят от массы частицы М. Эти потери для всех частиц в области малых скоростей β<<1 (но больших по сравнению с «внутриатомными скоростями» электронов) изменяется как 1/β² , т.е. по мере замедления нерелятивистской частицы её потери на ионизацию резко увеличиваются. С ростом β они достигают минимума, поэтому умеренно релятивистскую частицу иногда называют «минимально ионизирующей». При дальнейшем росте β потери медленно (~ln β) растут.

Зависимость (-dE/dx) от свойств среды определяется отношением Z_а/A, близким к 1/2 для большинства веществ, что приводит к слабой их зависимости от материала. В этом состоит практичность выражать потери энергии в массовых единицах. Влияние среднего потенциала ионизации I, стоящего «под логарифмом», мало. Для однозарядной минимально ионизирующей частицы потери составляют от 1 до 2 МэВ см²/г.

Экспериментально было замечено, что необходимы поправки к формуле Бете-Блоха. Для вычисления средних удельных потерь энергии релятивистских тяжелых ионовследует использовать формулу Бете - Блоха с поправками: поправка на эффект плотности Мотта и Блоха, обусловленный поляризацией среды заряженной частицей - при умеренно релятивистских энергиях, и поправка Линдхарда - Соренсена на конечный размер ядра-снаряда - при высоких энергиях.

Если частица движется в веществе, состоящем из нескольких сортов атомов, то ионизационные потери энергии принято характеризовать эффективным порядковым номером Z_эфф. Он равен порядковому номеру однородного вещества, в котором удельные потери такие же, как и в неоднородном веществе. Он может быть не равным целому числу, как у элементов. Так, воздуху приписывается Z_эфф = 7, 64 .

Важной характеристикой прохождения тяжелых заряженных частиц в веществе является полный пробег частицы, то есть путь R, который заряженная частица проходит до остановки и полной потери кинетической энергии:

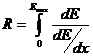(3.85).

Процесс ионизации происходит в две стадии. На первой стадии падающая частица непосредственно выбивает из атомов электроны. Это так называемая первичная ионизация. Достаточно энергичные из них (кэВ- и даже МэВ-ные), называемые δ-электронами, в свою очередь производят вторичную ионизацию. Полный пробег R δ-электрона в веществе, измеренный вдоль его траектории, может быть вычислен интегрированием формулы Бете-Блоха на длине пробега и приравниванием полученного интеграла и начальной энергии.

Взаимодействуя в основном с атомными электронами, тяжелые заряженные частицы мало отклоняются от направления своего первоначального движения, поэтому пробег тяжелой частицы R измеряют расстоянием по прямой от источника частиц до точки их остановки. Средний пробег R_α моноэнергетических α - частиц обычно рассчитывают по эмпирическим формулам. В воздухе при нормальных условиях:

R_α=а E_α^к (3.86),

где R_α - пробег в см; E_α - кинетическая энергия α - частиц в МэВ. Константы a=0,318, к = 1,5 для естественных α - излучателей (4<E_α<9МэВ) и a = 0,148, к = 1,8 для α - частиц с более высокими энергиями E_α≤200 МэВ

Отношение линейных пробегов в воздухе двух типов частиц с одинаковой начальной энергией, пропорционально отношению удельных потерь энергии частиц:

R₁/R₂= 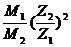(3.87),

где M и Z соответствующие массы и заряды частиц. Это соотношение позволяет, зная пробег одной из них, вычислять пробеги других типов частиц. А если вместо линейного пробега использовать массовый, выражаемый в (г/см²), то тогда этот пробег мало зависит от состава вещества, так как отношение A/Z для многих веществ изменяется мало, то и массовый пробег для этих веществ почти постоянен.

Дата добавления: 2018-05-13; просмотров: 1110; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!