Ионизационные потери энергии.

Ионизационные потери релятивистских электронов с энергией (Е^/>0,01 МэВ) описываются формулой:

 

      (- dЕ / dx)_ион= 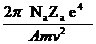 [ln  –

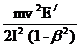  - (2 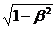-1+ β²) ln2 + 1- β²+ 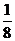(1- 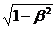)²] (3.94),

 

в которой  обозначения аналогичны приведенным выше для формул (3.83), (3.84) за исключением того, что v - скорость электрона.

Энергетическая зависимость ионизационных потерь сводится к их уменьшению с увеличением энергии электрона до кинетических энергий, равных удвоенной энергии покоя электрона, а затем медленному подъему примерно по логарифмическому закону.

Образование тормозного излучения и радиационные потери энергии.

При больших энергиях электроны начинают эффективно терять энергию за счет все большего и большего возрастания роли тормозного излучения. Радиационные потери наблюдаются при ускоренном движении свободной заряженной частицы в электрическом поле ядра. Пролетая вблизи ядра, заряженная частица отклоняется от своего первоначального направления под действием кулоновской силы, пропорциональной ее массе и ускорению. Свободный заряд, движущийся с ускорением, излучает электромагнитные волны, энергия которых пропорциональна Z²/M². Отсюда следует, что радиационные потери тяжелых заряженных частиц значительно меньше радиационных потерь электронов и позитронов.

Точный расчет дифференциальных микроскопических поперечных сечений образования тормозного излучения при прохождении электронов встречает большие трудности, поэтому используются различные приближения, при этом зависимость дифференциальных поперечных сечений от начальной энергии электрона Е^/, энергии образующегося кванта Е_γ определяется степенью экранирования поля ядра атомными электронами. Степень экранирования определяется величиной:

 

                γ=100Е_γmc²/[(E^/+mc²) (E+mc2)Z^1/3        (3.97),

 

где Е=Е^/ - Е_γ. Установлено 3 степени экранирования: γ<2 – неполное, 2< γ<15 – промежуточное и γ>15 – полное.

При γ>>1:

σ_рад(Е^/,Е,Е_γ) =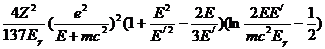

                                                                                                   (3.98)

при γ<2

σ_рад(Е^/,Е,Е_γ)= 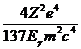[ 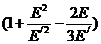ln183Z^-1/3+ 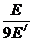] (3.99).

 

1/137, входящее в выражения, – постоянная тонкой структуры. Радиационные потери энергии электрона на единице пути можно рассчитать, интегрируя произведения энергии фотона на макроскопическое поперечное сечение образования тормозного излучения по энергиям фотонов. Они растут пропорционально кинетической энергии электронов Е^/ и могут быть оценены по следующим формулам:

при E^/ << mc²

 

(- dЕ / dx)_рад=(16E^/ Z_а r₀² N_а)  / А*137*3                     (3.100)

 

При  mc²<<E^/<<137 m_ec² Z^-1/3

 

(- dЕ / dx)_рад= (E^/ Z_а r₀² N_а  / 137А) (4ln(2E^// mc²) – 4/3   (3.101)

 

при E^/ >> 137 mc² Z^-1/3

 

(- dЕ / dx)_рад= (E^/ Z_а r₀² N_а  / 137А) (4ln(183/ Z^-1/3) +2/9  (3.102)

 

здесь обозначения такие же, как и в выше приведенных формулах.

Радиационные потери при больших энергиях электронов можно описать с помощью следующего простого соотношения:

 

  (-dE/dx)_рад = E^//L_r, или Е = Е₀ е^-x/Lr                         (3.103)

 

Величина L_r называется радиационной длиной. Радиационная длина - средняя толщина вещества, на которой энергия электрона уменьшается в е раз:

 

   1/L_r = 4(ħ/mc)²nZ(Z + 1)α ³ln(183/Z^1/3)                     (3.104)

 

Зависимость ионизационных и радиационных потерь от энергии электронов и атомного номера материала показана на рис.3.17.

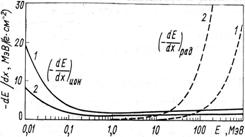
Рис.3.17. Массовые ионизационные и радиационные потери энергии электронов в воздухе (1) и свинце (2).

 

Учитывая слабую зависимость ионизационных потерь от энергии электронов и практически линейную зависимость потерь на радиацию от энергии электронов, была получена взаимосвязь удельных радиационных и ионизационных потерь энергии электронов, описываемая формулой Бете-Гайтлера:

                

                 (dЕ/dх)_рад/(dE/dx)_ион= ZE/800    (3.105),

 

где Е выражается в МэВ, Z - средний заряд ядер атомов среды.

Критическая энергия, при которой величина удельных радиационных потерь равна величине удельных ионизационных потерь, равна, например, для железа (Z=26) 31 МэВ, а для свинца (Z = 82) – 9,8 МэВ.

Масса электронов значительно меньше массы тяжелых заряженных частиц, что сказывается на характере их движения в веществе. При столкновении с атомными электронами и ядрами электроны значительно отклоняются от первоначального направления движения и движутся по извилистой траектории в отличие от прямолинейной для тяжелых заряженных частиц.

Характер ослабления плотности потока моноэнергетических электронов от плоского мононаправленного источника в среде демонстрирует рис. 3.18.

 

 

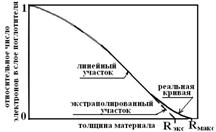Рис.3.18.Кривая поглощения электронов в среде.

 

Можно выделить два участка  на  представленной зависимости: практически линейный участок кривой ослабления и нелинейный в конце пробега. Основываясь на приведенной зависимости, для электронов вводится понятие максимального R_макс и экстраполированного R_экс пробега в веществе. Максимальный пробег электрона определяется толщиной слоя вещества, при которой ни один электрон не выйдет за его пределы. Экстраполированный или практический пробег находится экстраполяцией линейной части кривой ослабления потока электронов в веществе к нулю. Экстраполированные пробеги электронов с энергией Е (МэВ) в веществе, выраженные в (г/см²), можно оценить по формулам:

 

R_экс = 0,526 · Е - 0,094         для 0,5 <Е≤ 3 МэВ 

           

R_экс = 0,15 · Е - 0,0028            для 0,03 <Е ≤ 0,15 МэВ (3.106).

 

Выраженный таким образом пробег не зависит от материала поглотителя. Максимальный пробег можно принять примерно на 30% увеличенному экстраполированному пробегу.

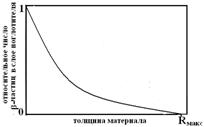Специфика ослабления в веществе плотности потока β-частиц (рис.3.19) в отличие от электронов обусловлена присутствием в спектре падающего на поглотитель излучения электронов с разными энергиями, определяемыми β-спектром излучения радионуклида.

 

 

Рис.3.18.Кривая поглощения β-частиц в среде.

 

 

Это приводит к практически экспоненциальному ослаблению плотности потока с ростом толщины поглотителя, приближаясь к нулю при некоторой толщине среды, равной максимальному пробегу R_макс. Исходя из этого при толщине поглотителя меньшей максимального пробега плотность потока β-частиц на глубине d, г/см², можно рассчитать по формуле:

 

                         φ (d)= φ₀ · exp (-μ_β d)            (3.107),

 

в которой φ₀ - плотность потока частиц при нулевой толщине, а μ_β – массовый коэффициент поглощения электронов, см²/г, который приближенно можно определить, зная максимальную энергию β-спектра  Е_βмакс по формуле μ_β≈22Е_βмакс.

       Максимальные пробеги β-частиц можно оценить, пользуясь приближенными формулами:

 

     для алюминия, мм R_макс ≈ 2,5 Е_βмакс             (3.108)

      для воздуха, м          R_макс ≈ 450Е_βмакс                     (3.109).

 

Максимальная энергия в выше приведенных формулах подставляется в МэВ.

 

Контрольные вопросы к § 3.5.

1. В чем специфика взаимодействия заряженных частиц с веществом?

2. Назовите основные процессы взаимодействия заряженных частиц с веществом.

3. Насколько велика анизотропия углового распределения упруго рассеивающейся заряженной частицы?

4. Как зависят ионизационные потери заряженной частицы от ее заряда и массы?

5. Как зависят ионизационные потери тяжелой заряженной частицы от свойств среды?

6. Что такое средний пробег тяжелой заряженной частицы?

7. В чем заключается разница в прохождении электронов и тяжелых частиц в веществе?

8. Как зависят радиационные потери от массы и заряда частицы?

9. Запишите соотношение между ионизационными и радиационными потерями для электронов.

10.Что такое максимальный и экстраполированный пробег электронов? 

11.В чем специфика ослабления в материале плотности потока β-частиц по сравнению с электронами?

12. Как оценить максимальные пробеги β-частиц в алюминии и воздухе, если известна максимальная энергия β-спектра?

 

---

Дата добавления: 2018-05-13; просмотров: 1272; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!