Кинематика рассеяния нейтронов

Важным моментом для расчета переноса нейтронов в веществе является изменение его энергии и направления движения при рассеянии на ядре, что позволяет определить дифференциальные эффективные поперечные сечения рассеяния нейтрона. Ответ на этот вопрос можно получить, рассматривая кинематику рассеяния нейтронов, причем представляется удобным решать эту задачу в лабораторной системе координат и в системе центра инерции. На рис.3.13 приведены схемы рассеяния нейтрона на ядре массой А в лабораторной системе координат и в системе центра инерции:

 

а                                                                   б

Рис.3.13. Схемы рассеяния нейтрона в лабораторной системе координат (а) и в системе центра инерции (б)

 

В соответствии с приведенными на рис. 3.13 обозначениями скоростей нейтрона и ядра запишем законы сохранения энергии и импульса в рассматриваемых системах, принимая массу нейтрона за единицу и обозначая энергию возбуждения ядра в результате рассеяния Е*:

 

в лабораторной системе координат            системе центра инерции

=                               (3.52)

=

При этом скорость центра инерции в лабораторной системе координат:

                                     (3.53)

Учитывая очевидное соотношение между скоростью налетающего нейтрона в системе центра инерции и в лабораторной системе координат

                                             (3.54),

 из закона сохранения энергии в системе центра инерции получим:

            v_c² = v^/_c ²- 2АЕ*/(А+1)           (3.55),

 

откуда следует, что при упругом рассеянии (Е*=0) скорость нейтрона в системе центра инерции, а, следовательно, и его кинетическая энергия не изменяются. Используя выражение (3.54), из (3.55) можно записать связь между скоростью рассеянного нейтрона в системе центра инерции и скоростью налетающего нейтрона в лабораторной системе координат:

 

       v_c² = А² v^{/ 2}/(А+1)² - 2АЕ*/(А+1)         (3.56).

 

Из диаграммы скоростей нейтрона в лабораторной системе координат и в системе центра инерции (рис.3.14) можно записать:

Рис. 3.14. Диаграмма скоростей нейтрона в разных системах координат

 

v²=v_c² +V_c²+2v_cV_c Сosθ_c (3.57),

 

а, переходя от скоростей нейтрона к его энергии, получим соотношение между энергией нейтрона до и после рассеяния:

 

. Е=Е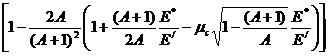^/  (3.58),

Беря проекции скоростей нейтрона на направление вектора на диаграмме скоростей нейтрона, получим соотношение между углами рассеяния нейтронов в рассматриваемых системах координат:

 

                  μ_s=(1+A μ_с)/ (1+2А μ_с+А²)^1/2            (3.59),

 

где μ_s , μ_с – косинусы углов рассеяния нейтрона в лабораторной системе координат и системе центра инерции соответственно.

Полученные соотношения (3.58) и (3.59) позволяют сделать важные для задач переноса нейтронов и защиты от них выводы о характере рассеяния нейтронов в разных материалах.

Соотношение (3.58) подтверждает сформулированное выше заключение о наличии энергетического порога сечения неупругого рассеяния. Этот процесс возможен, если энергия нейтронов удовлетворяет условию:

 

                              Е^/ > Е^*                       (3.60).

 

В противном случае происходит упругое рассеяние, для которого связь между энергиями нейтрона до и после рассеяния записывается в виде:

 

                          Е=Е^/                    (3.61).

 

Из формулы (3.61) следует, что при угле рассеяния θ_с =0⁰ (рассеяние прямо вперед) энергия нейтрона после рассеяния равна его первоначальной энергии, а при рассеянии на угол θ_с =180⁰ (рассеяние прямо назад) энергия рассеянного нейтрона минимальна и равна:

                        Е_мин= Е^/                          (3.62).

 

Величина α = (А-1)²/(А+1)², характеризующая максимальный сброс энергии нейтрона при однократном упругом рассеянии, широко используется в теории замедления нейтронов и показывает, что с ростом атомного номера материала А уменьшается максимальный сброс энергии нейтрона при однократном рассеянии; этим объясняется использование легких материалов (вода, углерод и т.д.) в качестве замедлителей нейтронов. Максимальный сброс энергии нейтрона наблюдается на ядре водорода (А=1); для него величина α=0.

Из формулы (3.59) видно, что при А>>1 μ_s = μ_с, таким образом, для средних и тяжелых материалов при изотропном угловом распределении рассеянных нейтронов в системе центра инерции их угловое распределение будет изотропным и в лабораторной системе координат. Напротив, для легких материалов будет наблюдаться анизотропия углового распределения в лабораторной системе координат, ярко выраженная для водорода, когда θ_s = θ_c/2, т.е. при рассеянии на водороде все нейтроны летят в полупространство с μ_s>0.

Для перехода от характеристик нейтронов, полученных в одной системе координат, к аналогичным в другой системе координат из кинематики можно записать следующие широко используемые формулы перехода:

 

         E=E_c+[(E+2μ_c(A+1) ]/(A+1)²

         μ_s= μ_{c +}                                        (3.63),

 

в которых энергии без нижнего индекса соответствуют их знаяениям в  лабораторной системе координат.

 

3.4.7. Специфика рассеяния тепловых нейтронов

При низких энергиях нейтронов (E<5 эВ) взаимодействие нейтронов с некоторыми материалами носит специфический характер, обусловленный переходом от ядерного взаимодействия к взаимодействию с молекулами или кристаллической решеткой вещества.

Когда дебройлевская длина волны нейтрона сравнима с расстоянием между плоскостями кристаллов, в кристаллических телах наблюдается дифракционное рассеяние нейтронов, которое можно отнести к когерентному рассеянию без изменения энергии. Нейтроны рассеиваются по направлениям, соответствующим росту амплитуд рассеянных когерентных волн. Характеристикой этого рассеяния является сечение когерентного рассеяния, которое с ростом энергии нейтрона переходит в сечение потенциального рассеяния на отдельном ядре при энергиях порядка 1 эВ. При энергии нейтронов ниже средней энергии теплового движения появляется возможность передачи энергии от кристаллической решетки нейтрону, что приводит к росту сечения когерентного рассеяния при увеличении температуры среды.

Если энергия сталкивающегося нейтрона меньше энергии связи атома в молекуле (единицы эВ), то атом не может быть выбит из молекулы, в итоге импульс при рассеянии передается всей молекуле. В итоге происходит рассеяние на связанном ядре, что дает сечение рассеяния на связанном ядре σ_in,n = σ_in (А+1)²/А², где σ_in –сечение рассеяния на свободном ядре. Видно, что этот эффект наиболее заметен для легких ядер и, например для водорода приводит к росту сечения рассеяния в 4 раза. Следует отметить, что при этом происходит возбуждение молекул, поэтому этот процесс можно отнести к неупругому рассеянию.

3.4.8. Дифференциальные микроскопические поперечные сечения рассеяния

Исходя из кинематики рассеяния нейтронов, формирование углового и энергетического распределения рассеянных нейтронов будет различаться для упругого и неупругого рассеяния. Следовательно, будет различаться и характер дифференциальных поперечных сечений этих процессов.

Упругое рассеяние. При упругом рассеянии существует однозначная связь между энергией и направлением движения рассеянного нейтрона.

Тогда, исходя из формулы (3.15), дифференциальное микроскопическое поперечное сечение упругого рассеяния на ядре массой А в системе центра инерции можно записать в виде:

 

 

dσ_el(Е^/→Е,μ_с)/dΩdE= δ(E– )

                                                                                                  (3.64).

Входящие в выражение (3.64) величины объяснены при описании формулы (3.15). При больших значениях А угловое распределение рассеянных нейтронов в системе центра инерции близко к изотропному и тогда формула (3.64) упрощается, так как индикатриса рассеяния g( 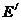,μ_c)=1. При этом становится равновероятным распределение рассеянных нейтронов по энергии в интервале от αЕ^/ до Е^/.

Таким образом, при изотропном угловом распределении рассеянных упруго нейтронов характеристики рассеянного нейтрона можно определить по формулам:

 

 Е= αЕ^/+ρ₁(1-α)E^/,     μ_c= -1+2 ρ₂ ,     φ=2π ρ₃                (3.65),

 

где ρ₁, ρ₂, ρ₃ - случайные числа, равномерно распределенные на отрезке. [0,1], а переход от μ_c к μ_s провести по формуле (3.59) или (3.63).

Учитывая тот факт, что угловое распределение рассеянных нейтронов в системе центра инерции более изотропно, чем в лабораторной системе координат, дифференциальные микроскопические сечения рассеяния нейтронов (в частности, индикатриса рассеяния) обычно в библиотеках констант представляется в системе центра инерции и для перехода к лабораторной системе координат используются матрицы перехода. Особенно это важно, когда индикатриса рассеяния представляется в виде разложения в ряд по полиномам Лежандра:

              g( 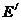,μ_c)=  (3.66),

где         g_l ( 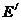)=2π .

Тогда для получения той же точности представления индикатрисы можно ограничиться меньшим числом членов ее разложения в ряд.

Неупругое рассеяние. Рассматривая дифференциальное микроскопическое поперечное сечение неупругого рассеяния, исходя из модели составного ядра, можно выделить две области по энергии нейтронов, специфичные для его поведения. При энергиях нейтронов, соответствующим энергиям изолированных низкоэнергетических уровней возбуждения ядра, спектр рассеянных нейтронов представляет собой набор дискретных энергий, а угловое распределение в первом приближении можно принять за изотропное, как в системе центра инерции, так и в лабораторной системе координат. Дифференциальное микроскопическое поперечное сечение неупругого рассеяния для этого диапазона энергий первичных нейтронов можно записать в виде:

                 σ_in( )/dΩdE=

(3.67),

 

где  - сечение неупругого рассеяния при энергии L-го возбужденного уровня ядра, Е_L^* - энергия L-го возбужденного уровня ядра.

C ростом энергии первичного нейтрона возбуждается все большее число уровней возбуждения ядра, перекрывающихся друг с другом, и энергетическое распределение рассеянных нейтронов переходит в непрерывное распределение. В итоге для этого энергетического диапазона дифференциальное микроскопическое поперечное сечение неупругого рассеяния запишется в виде:

dσ_in( )/dΩdE= σ_in(Е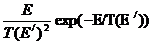^/) (3.68),

где Т - ядерная температура, зависящая от первоначальной энергии нейтрона и определяемая соотношением:

 

                              Т² ≈ Е^//а               (3.69),

 

с постоянной а, зависящей от атомного номера ядра и изменяющейся от 0,45 до 12 при изменении А от 27 до 231.

Следует отметить, что процесс неупругого рассеяния сопровождается фотонным излучением, обусловленным переходом возбужденного ядра в основное состояние. Спектр испускаемых фотонов зависит от энергетических уровней возбужденного ядра: при возбуждении низколежащих изолированных уровней испускаются один, два высокоэнергетичных фотона, при плотно расположенных высоких уровнях возбуждения число фотонов увеличивается и их спектр приближается к непрерывному. Максимальная энергия фотонов неупругого рассеяния не превышает, как правило, 4-5 МэВ.

Рассеяние на молекулах и кристаллической решетке.   При прохождении теплового нейтрона с энергией ниже примерно 5 эВ в среде нельзя пренебрегать его взаимодействием на атомном уровне и не учитывать влияния других атомов, и движения атома, на котором происходит взаимодействие; нельзя пренебрегать эффектом химических связей в молекулах и кристаллической структурой вещества. Эти процессы взаимодействия нейтронов при их термализации учитываются изменениями микроскопических поперечных сечений рассеяния нейтрона для некоторых материалов в диапазоне энергий нейтронов ниже 5 эВ, где эти процессы существенно влияют на распространение нейтронов. Полное микроскопическое поперечное сечение взаимодействия нейтрона складывается тогда из суммы двух частей: микроскопического поперечного сечения захвата нейтрона, представляемое в обычных библиотеках констант, и дополнительно рассчитываемыми микроскопическими поперечными сечениями когерентного и некогерентного упругого рассеяния и некогерентного неупругого рассеяния.

  Дифференциальное микроскопическое поперечное сечение когерентного упругого рассеяния на порошкообразных кристаллических материалах может быть представлено формулой:

 

                                                                                                 (3.70),

в которой: T - температура замедлителя (K), E_i - энергия Брегговских границ (эВ); s_i - коэффициенты, пропорциональные структурным факторам (эВ-барн), μ_si=1-2E_i/E -характеристический угол рассеяния для соответствующей совокупности плоскостей кристаллической решетки. Энергия Брегговских границ и структурные факторы рассчитываются из свойств кристаллической решетки и амплитуд рассеяния для различных атомов в ячейках кристаллической решетки.

Дифференциальное микроскопическое поперечное сечение некогерентного упругого рассеяния для материалов типа полиэтилен или гидрид циркония может описываться в виде:

 

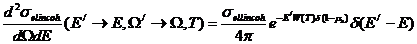
                                                                                                    (3.71)

 

где σ_elincoh - характеристическое предельное микроскопическое поперечное сечение (барн), W- интеграл Дебая-Уоллера, поделенный на атомную массу (1/эВ), а все другие переменные как в (3.70). При этом интегральное микроскопическое поперечное сечение равно:

 

     σ_elincoh =           (3.72) ,

 

что при низких энергиях нейтрона дает совпадение характеристического предельного поперечного сечения с полным.

Дифференциальное микроскопическое поперечное сечение некогерентного неупругого рассеяния тепловых нейтронов для замедляющей молекулы может быть представлено в виде:

 

                                                                                                   (3.73),

где n - типы атомов, а M_n – их количество в молекуле или ячейке кристаллической решетки (например, для H₂O, N = 1);

 β =(Е^/ – Е) / кТ – изменение энергии, α=(Е^/+Е - 2μ_s )/А₀ кТ –изменение импульса нейтрона, σ_in,n = σ_in (А_n+1)² / А_n² – микроскопическое поперечное сечение связанного атома типа n, а σ_in – аналогичное сечение неупругого рассеяния на свободном атоме типа n; A_n – масса атома типа n, А₀ – масса основного рассеивающего атома в молекуле. S(α,β,T) - функция рассеяния, которая может быть представлена либо в виде таблицы с различными законами интерполяции для основного атома, либо аналитически в виде модели идеального газа или приближения наикратчайшего времени столкновения.

При использовании модели идеального газа предполагается, что среда может быть аппроксимирована свободным газом, в котором в области масс ядер и энергий нейтронов, где существенны термализационные эффекты, микроскопическое поперечное сечение рассеяния при нулевой температуре слабо зависит от скорости нейтрона и температуры среды. В кинематике рассеяния нейтрона учитывается движение ядра мишени и S(α,β,T) для модели идеального газа имеет вид:

 

                     S(α,β,T) =              (3.74).

 

Расчет функции рассеяния проведен для ограниченного набора материалов (вода, графит, бериллий, полиэтилены и др.) и диапазона энергий нейтронов, где тепловые процессы значительны.

Для приближения наикратчайшего времени столкновения:

 

S(α,β,T) =

                  (3.75),

 

где T_эфф(T) - эффективная температура, а другие символы описаны выше.

 

3.4.9. Ядерные реакции.

Если энергетически возможно, то при прохождении нейтронов через вещество происходят реакции с образованием заряженных частиц. В основном они используются для регистрации нейтронов и практически не играют роли с точки зрения радиационной безопасности или защиты от нейтронов. Однако некоторые из них необходимо учитывать и при проектировании защиты. Рассмотрим некоторые из них.

Реакции с образованием протонов, (n,р) - реакции:

 

                                                       ¹_on + ^A_ZX 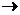^A_Z-1X+¹₁ p     (3.76),

одна из которых                ¹_on + ³₂Не 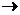³₁Н+¹₁p      (3.77)

              

широко применяется для регистрации нейтронов в счетчиках, наполненных ³Не (σ(n,p)= 5400 барн для тепловых нейтронов), а вторая

                                                        ¹_on + ¹⁴₇N  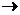¹⁴₆C+¹₁p    (3.78)

 

имеет сечение для тепловых нейтронов σ(n,p) = 1,75 барн и приводит к образованию естественного ¹⁴С (Т_1/2=5730 лет) в атмосфере Земли нейтронами космического происхождения.

Реакции с образованием α-частиц, (n, α ) - реакции:

 

                                                          ¹_on + ^A_ZX 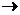^A_Z-1X+⁴₂Не   (3.79)

 

используются не только для регистрации тепловых нейтронов, например,

                                                        ¹_on + ¹⁰₅В 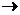⁷₃Li+⁴₂Не  (3.80),

 

имеющая микроскопическое поперечное сечение для тепловых нейтронах σ(n,α)= 3840 барн и широко применяемая для регистрации тепловых нейтронов в различных борных счетчиках и ионизационных камерах, но и как выступающие в качестве конкурирующих радиационному захвату в защитных материалах.

  При проектировании защиты важны реакции (n,γ), ведущие к образованию радиоактивных нуклидов – продуктов активации в оборудовании. Примером такой реакции может служить реакция захвата нейтрона ⁵⁹Co(n,γ)⁶⁰Co с образованием долгоживущего радионуклида, испускающего фотоны с энергиями 1,17 и 1,33 МэВ.

 

3.4.10. Полные эффективные микроскопические поперечные сечения взаимодействия нейтронов с веществом.

Рассматривая поведение полногомикроскопического поперечного  сечения взаимодействия нейтронов разных энергий с веществом можно отметить, что в отличие от сечений взаимодействия фотонов с веществом не представляется возможным простыми формулами описать эти сечения, как в зависимости от атомного номера материала, так и от энергии нейтрона. Однако на основе изложенного выше можно проследить некоторые закономерности, позволяющие понять специфику взаимодействия нейтронов с разными материалами для разных энергетических групп нейтронов.

В области тепловых и медленных нейтронов для материалов слабо поглощающих нейтроны полное микроскопическое поперечное сечение практически постоянно и определяется сечением потенциального рассеяния, которое не зависит от энергии (равно ≈7πА^2/3) и растет с атомным номером материала рассеивателя (рис.3.15).

Рис.3.15. Зависимость полных микроскопических поперечных сечений взаимодействия нейтронов для разных ядер от энергии в области тепловых и медленных нейтронов.

 

Для элементов, заметно поглощающих нейтроны, основной вклад в полное микроскопическое сечение дает сечение поглощения, которое с ростом энергии уменьшается обратно пропорционально скорости нейтрона, т.е. ~1/ 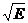. Следует отметить, что для некоторых материалов сложного состава (вода, полиэтилен, окись бериллия, гидрид циркония и др.) существенную роль при энергиях нейтронов ниже 5 эВ играет когерентное и некогерентное рассеяние нейтронов на молекулах и кристаллической решетке, что оказывает существенное влияние на характер распространения низкоэнергетичных нейтронов в этих средах.

При увеличении энергии нейтронов практически для всех ядер наблюдается резонансная структура полного микроскопического поперечного сечения, обусловленная при небольших энергиях редко расположенными уровнями возбуждения ядра, все более часто повторяющимися с ростом энергии (рис.3.16).

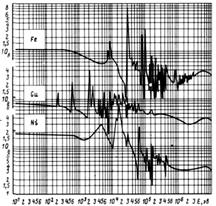
Рис.3.16. Зависимость полных микроскопических поперечных сечений взаимодействия промежуточных и быстрых нейтронов с различными ядрами от энергии нейтронов.

 

В этой области энергий на постоянное сечение потенциального рассеяния накладываются резонансы упругого резонансного рассеяния и радиационного захвата, описываемые формулой Брейта-Вигнера. Для тепловых нейтронов преобладающим является радиационный захват, но затем с ростом энергии, так как нейтронная ширина резонанса Г_n растет пропорционально скорости нейтрона, а радиационная Г_γ уменьшается как 1/v, то на постоянное сечение потенциального рассеяния накладываются резонансы упругого резонансного рассеяния. Это характерно для промежуточной области энергий нейтронов, часто называемой резонансной.

В зависимости от атомного номера для легких ядер резонансная структура сечения рассеяния проявляется только при энергиях выше 100 кэВ, для средних – несколько кэВ, для нескольких тяжелых ядер она наблюдается уже при энергиях ниже 0,1 кэВ.

С ростом энергии нейтронов уровни энергии составного ядра начинают перекрываться (у тяжелых ядер начиная с ~ 10 кэВ и выше). В результате составное ядро образуется с одинаковой вероятностью при любой энергии нейтронов, резонансная картина пропадает, и сечение упругого рассеяния монотонно убывает с ростом энергии нейтронов.

При энергии нейтронов выше примерно 0,5 МэВ становится возможным процесс неупругого рассеяния нейтронов, особенно заметный для тяжелых ядер, микроскопическое поперечное сечение которого растет с ростом энергии нейтрона, переходя к σ_t =2π(R+ )² , где R - радиус ядра, а - дебройлевская длина волны нейтрона. Главная особенность быстрой области энергий нейтронов состоит в практическом отсутствии радиационного захвата, и полное микроскопическое сечение взаимодействия полностью определяется сечениями упругого и неупругого рассеяния. При энергии нейтронов Е>8 МэВ сечение рассеяния на тяжелых ядрах снижается из-за конкуренции реакций (n,2n) и (n, f).

 

Контрольные вопросы к § 3.4.

1. В чем заключается разница между прямым взаимодействием нейтронов и через механизм составного ядра?

2. Чем объясняется резонансная структура поперечного сечения образования составного ядра?

3. Как меняется частота резонансов и их амплитуда с ростом энергии нейтронов?

4. Что описывается формулой Брейта-Вигнера?

5. Чем отличаются поперечные сечения упругого и неупругого рассеяния нейтронов?

6. Чем отличаются скорости нейтрона до и после упругого рассеяния в системе центра инерции?

7. Чему равна минимальная энергия нейтрона после упругого рассеяния на ядре массой А?

8. Показать, что микроскопическое поперечное сечение неупругого рассеяния имеет энергетический порог.

9. В чем состоит специфика рассеяния тепловых нейтронов?

10. В чем заключается разница в описании дифференциального микроскопического поперечного сечения неупругого рассеяния для энергий нейтронов вблизи порога реакции и при высоких энергиях нейтронов?

11.Объясните зависимость полного микроскопического поперечного сечения взаимодействия нейтронов с веществом от их энергии.

12.Чему равна вероятность нейтрона с энергией Е^/ , изотропно упруго рассеявшегося на ядре массой А, иметь энергию Е после рассеяния?

 

---

Дата добавления: 2018-05-13; просмотров: 1497; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!