Эффективные поперечные сечения взаимодействия.

⇐ ПредыдущаяСтр 5 из 39Следующая ⇒

Для количественной оценки вероятности того или иного типа взаимодействия излучения с веществом введено понятие эффективного поперечного сечения взаимодействия. Эффективные поперечные сечения могут быть микроскопическими и макроскопическими, интегральными и дифференциальными.

Микроскопические и макроскопические эффективные поперечные сечения взаимодействия.

Микроскопическое эффективное поперечное сечение взаимодействиярассматривает взаимодействие излучения на уровне одного атома или ядра. Определим его физический смысл на примере взаимодействия частиц с ядрами среды. Пусть на тонкий плоский однородный слой неперекрывающихся ядер вещества толщиной в 1 ядро с плотностью ядер N_яд (ядер/см²) падает перпендикулярно однородный поток частиц, плотность потока которых равна φ (см^-2 с^-1) (рис.3.1).

Рис.3.1. Схема определения микроскопического эффективного поперечного сечения взаимодействия

Если при прохождении частицами слоя произошло N_i i-го типа взаимодействий на площади см² (взаим./см² ), то тогда вероятность i-го типавзаимодействий (доля частиц, испытавших такое взаимодействие из числа упавших на см² поверхности) равна: р = N_i / φ. Отсюда эта вероятность i-го типа взаимодействия, отнесенная к 1 ядру мишени р / N_яд называют эффективным поперечным микроскопическим сечением i-го типа взаимодействия и обозначают σ_i_.:

σ_i = N_i/ φ N_яд (3.2).

Фактически выражение (3.2) определяет число i-го типа взаимодействий, отнесенное к 1 ядру мишени и 1 падающей на слой частице. Если равенство (3.2) переписать в виде σ_i N_яд /1см²= р=N_i /φ, то становится очевидным, что стоящее справа выражение характеризует долю частиц, испытавших i-ый тип взаимодействия, а слева долю площади из 1см², участвующей во взаимодействии, т.е. вероятность того, что из площади мишени 1 см²площадь σ_i N_яд участвует в i-ом типе взаимодействия со сто процентной вероятностью. Если эту площадь разделить на N_яд, то тогда σ_i будет соответствовать площади ядра, участвующей в i-ом типе взаимодействия. Следовательно, микроскопическое эффективное поперечное сечение взаимодействия имеет размерность площади (потому и называется поперечным сечением) и лишь характеризует вероятность взаимодействия, но не равно ей. В системе СИ микроскопическое эффективное поперечное сечение взаимодействия измеряется в м², в ядерной физике для измерения сечений используется см²или, учитывая малость абсолютного значения сечений, специальная единица, называемая барн (б), 1б=10^-28м². Эффективное поперечное сечение i-го типа взаимодействия называют парциальным, в отличие от полного, представляющего сумму парциальных сечений всех возможных типов взаимодействия. Часто для краткости слово эффективное, как и поперечное опускают в названии сечения.

Считая, что отдельные типы взаимодействия независимы друг от друга, можно говорить об аддитивности парциальных микроскопических поперечных сечений взаимодействия по типу взаимодействий и тогда полное микроскопическое эффективное поперечное сечение взаимодействия на к-ом ядре или атоме:

(3.3),

где I – число возможных типов взаимодействия данного вида излучения с ядром или атомом среды.

Учитывая, что расстояния между ядрами или атомами значительно превосходят размеры ядер или атомов, взаимодействия в большинстве случаев можно рассматривать как независимые процессы на разных ядрах или атомах среды, через которую проходит излучение, и, таким образом, можно ввести понятие полного макроскопического эффективного поперечного сечения взаимодействия излучения с единицей объема или массы вещества, как сумму сечений отдельных ядер или атомов, находящихся в этом объеме или массе:

; (3.4).

В формулах (3.4): , число ядер к-го материала в единице объема (см³) или единице массы (г) соответственно, 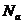= 6,02х10²³ (г моль)^-1 - число Авогадро, - атомная масса материала, - плотность материала (г/см³). Эти полные макроскопические поперечные сечения можно соответственно назвать линейными или массовыми и они обычно при указанных выше размерностях входящих величин измеряются в см^-1 или см²/г. Аналогичные соотношения можно записать и для парциальных макроскопических поперечных сечений i-го типа взаимодействия на к-ом материале, если в формулах (3.4) заменить на .

Используя тоже свойство аддитивности сечений, можно определить макроскопическое эффективное поперечное сечение взаимодействия вещества, представляющего гомогенную смесь различных материалов:

; (3.5),

где , - полные макроскопические эффективные сечения взаимодействия излучения с веществом смеси, , р^m_k - объемная и весовая доля к-го материала в смеси, , 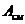- плотность и атомная масса смеси материалов.

Рассмотрим физический смысл введенных полных макроскопических поперечных сечений взаимодействия излучений с веществом на примере прохождения излучения через слой материала, на который подобно рис 3.1 падает однородный поток частиц, плотность потока которых равна φ₀ (см^-2 с^-1.). Если полное макроскопическое эффективное поперечное сечение взаимодействия излучения с веществом равно , то число взаимодействий этих частиц в элементе объема dv=1cм²dx вещества будет равно dv φ (x) , где φ (x) – плотность потока частиц на расстоянии x от передней поверхности вещества. Одновременно эта величина будет равна убыли частиц при прохождении слоя dx, т.е.

d φ (x) = dx φ (x). (3.6).

Из уравнения (3.6) следует закон ослабления нерассеянногоизлучения в веществе

φ (x)= φ₀ exp(- x) (3.7),

в котором в качестве характеристики ослабления излучения выступает полное макроскопическое эффективное поперечное сечение взаимодействия. С другой стороны из выражения (3.7) легко определяется вероятность частице пройти в веществе путь длиной х без взаимодействия, т.е.

р(х) = φ (x)/ φ₀ = exp(- x) (3.8),

которая позволяет определить среднюю длину пробега частицы до столкновения:

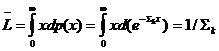(3.9)

Таким образом, величина, равная обратному значению полного макроскопического эффективного поперечного сечения взаимодействия определяет среднюю длину пробега частицы в данном веществе. Такие же величины для макроскопических парциальных поперечных сечений будут определять среднюю длину пробега частицы до соответствующего i-го взаимодействия.

Эффективные поперечные сечения взаимодействия зависят не только от вида излучения, типа взаимодействия и материала, но и от энергии частиц или квантов, участвующих во взаимодействии. Знание этих зависимостей в совокупности со знанием пространственно-энергетических распределений плотности потока частиц в веществе позволяет рассчитывать любые функционалы, характеризующие процессы, проходящие в веществе под действием излучения. Например, число столкновений N частиц с энергией Е, происходящих в элементе объема dV вещества, характеризуемого полным эффективным поперечным макроскопическим сечением взаимодействия (E), при плотности потока частиц в этом элементе объема φ(Е) равно:

N= (E) φ(Е)dV (3.10).

3.2.2. Дифференциальные и интегральные эффективные поперечные сечения взаимодействия

Введенные выше эффективные поперечные сечения взаимодействия излучений с веществом характеризуют возможность того или иного типа взаимодействия, но не определяют параметры излучения после взаимодействия. Поэтому они называются интегральными сечениями.

В отличие от них дифференциальные эффективные поперечные сечения взаимодействия, например, при рассеянии частицы определяют энергию рассеянной частицы и ее направление движения относительно направления движения первичной частицы. В случае, если в процессе взаимодействия образуется вторичное излучение, отличающееся от вида первичного, например, образуется фотон в реакции взаимодействия нейтрона с ядром, то дифференциальное эффективное поперечное сечение определяет не только вероятность такого события, но и дает сведения об угловом и энергетическом распределении образующегося вторичного излучения.

Таким образом, дифференциальное эффективное микроскопическое поперечное сечение рассеяния dσ_s( )/dEdΩ характеризует для данного вида излучения вероятность частице с энергией Е^/, летящей в направлении 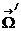испытать рассеяние, после которого она будет иметь энергию E на единичный интервал энергий и полетит в направлении в единичный телесный угол. Размерность дифференциального эффективного микроскопического поперечного рассеяния - м²эВ^-1ср^-1.

Обозначив через μ_s косинус угла рассеяния, т.е. косинус угла между векторам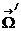и и , это сечение можно переписать в виде:

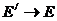dσ_s ( )/dEdΩ= σ_s (Е^/)p( )g ( 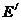,Е, μ_s) (3.11),

который описывает связь между эффективным дифференциальным и интегральным поперечными сечениями взаимодействия через вероятность при рассеянии поменять энергию с Е^/ на Е - p( 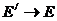) и вероятность изменить направление движения на угол θ_s, косинус которого равен μ_s_, - g ( 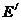, Е, μ_s).

Проинтегрировав обе части выражения (3.11) по всем возможным энергиям рассеянных частиц и всем направлениям их полета, получим при условии азимутальной симметрии рассеяния:

     μ_sdσ_s( )/dEdΩ =σ(Е^/)=

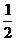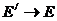     = σ (Е^/) μ_s p( )g ( 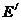,Е, μ_s)        (3.12)

условие нормировки для функций p( 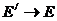) и g ( 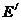,Е, μ_s):

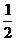
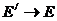   μ_s p( ) g ( 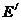,Е, μ_s)=1            (3.13)

При упругомрассеянии из законов сохранения энергии и импульса следует однозначная связь между энергией рассеянной частицы Е и углом рассеяния θ_s. В этом случае эффективное дифференциальное микроскопическое поперечное сечение упругого рассеяния приобретает следующий вид:

dσ_el( )/dEdΩ= σ_el (Е^/)g( 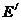,μ_s) δ(E – k(E^/, μ_s)) (3.14),

где δ(E – k(E^/, μ_s)) – дельта-функция по энергии, которая при интегрировании по энергии рассеянных частиц дифференциального эффективного поперечного сечения обращается в 1. Таким образом, при упругом рассеянии условие нормировки для вероятности частице с энергией Е^/ рассеяться на угол θ_s приводится к виду:



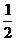
                    μ_s g ( 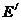, μ_s)=1            (3.15)

Следует отметить, что при изотропном угловом распределении рассеянных упруго частиц g ( 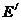, μ_s) не зависит от угла рассеяния и, следовательно, из (3.15) g ( 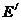, μ_s)=1. Отличие функции g ( 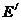, μ_s) от 1 характеризует отличие углового распределения рассеянных частиц от изотропного.

В общем случае функция g ( 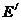,Е, μ_s) получила название индикатриса рассеяния, и ее знание позволяет определить дифференциальное эффективное поперечное сечение рассеяния.

В случае образования в процессе взаимодействия вторичного излучения, отличающегося от рассматриваемого, например, образование фотонов при захвате или неупругом рассеянии нейтрона на ядре энергетические и угловые характеристики этого вторичного излучения будут определяться дифференциальным микроскопическим поперечным сечением реакции, в результате которой это вторичное излучение возникает. Например, для реакции (n,γ) оно будет иметь вид:

dσ_n_,_γ( )/dE_γ dΩ_γ = dσ_n_,_γ (Е^/) p( )

                      g ( )                        (3.16).

При этом функция p( ) характеризует вероятность того, что при захвате нейтрона с энергией образуется n_γ фотонов с энергией , а функция g ( ) – есть вероятность образовавшимся фотонам полететь в единичный телесный угол в направлении относительно направления движения первичного нейтрона .

Знание дифференциальных сечений взаимодействия излучений с веществом необходимо для решения задач их переноса в веществе с учетом многократных столкновений с ядрами или атомами.

Многочисленные данные, как по интегральным, так и дифференциальным микроскопическим эффективным сечениям взаимодействия разных видов излучения с веществом опубликованы в виде справочников и таблиц. Для удобства пользования этими данными формируются библиотеки оцененных ядерных данных, постоянно обновляемые и пополняемые новой информацией по сечениям взаимодействия.

Контрольные вопросы к § 3.2

1. Какую площадь характеризует микроскопическое эффективное поперечное сечение взаимодействия?

2. Чем отличается полное эффективное поперечное сечение от парциального?

3. Укажите отличия в макроскопических эффективных поперечных сечениях, измеряемых в см^-1и см²/г.

4. Чему равно число столкновений в объеме dV вещества, имеющего полное эффективное поперечное макроскопическое сечение взаимодействия Σ, см^-1 при плотности потока падающего излучения 1 см^-2с^-1?

5. Как связаны между собой средняя длина пробега в веществе и полное эффективное поперечное макроскопическое сечение?

6. Запишите формулу для расчета числа рассеяний, происходящих в единице объема вещества, имеющего сечение рассеяния Σ_s при плотности потока частиц в этом объеме φ.

7. Какие параметры рассеянного излучения характеризует дифференциальное эффективное микроскопическое поперечное сечение рассеяния?

8. Чем обусловлено появление δ-функции в дифференциальном эффективном поперечном микроскопическом сечении при упругом рассеянии?

9. Что такое индикатриса рассеяния?

10.Чему равна индикатриса упругого рассеяния при изотропном угловом распределении рассеянных частиц?

Дата добавления: 2018-05-13; просмотров: 961; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!