Глава 2. Характеристики полей ионизирующих излучений
Дифференциальные и интегральные
характеристики полей излучений.
Поле излучений – пространственно-временное распределение ионизирующего излучения в рассматриваемой среде, а точнее – это совокупность нейтронов, фотонов или заряженных частиц в среде, характеризуемых распределением по энергии, времени, пространству и направлению движения.
Характеристики полей излучений подразделяются на 2 категории: потоковые и токовые.
Потоковые характеристики полей излучений.
Наиболее подробной характеристикой поля излучения является дифференциальная плотность потока частиц, описывающая пространственно-энергетическое, угловое и временное их распределение в среде.
Выделим элемент объема среды dV, положение которого в пространстве определяется вектором  (см. рис.2.1.).
(см. рис.2.1.).
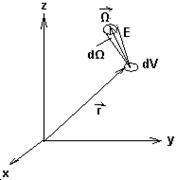
Рис.2.1. К определению дифференциальных характеристик поля излучения.
Рассмотрим частицы или фотоны, находящиеся в этом элементе объема в момент времени t, выделив среди них те, которые имеют энергию в диапазоне от Е до Е+dE и движутся в направлении  в элемент телесного угла dΩ. Если dN = n (
в элемент телесного угла dΩ. Если dN = n (  , E,
, E,  , t) dV dE dΩ – есть число частиц или фотонов в элементе объема dV в момент времени t с кинетической энергией в интервале от Е до Е+dЕ, движущихся в направлении
, t) dV dE dΩ – есть число частиц или фотонов в элементе объема dV в момент времени t с кинетической энергией в интервале от Е до Е+dЕ, движущихся в направлении  в элемент телесного угла dΩ , то тогда величина n (
в элемент телесного угла dΩ , то тогда величина n (  , E,
, E,  , t) – есть дифференциальная плотность частиц или пространственно-угловое и энергетическое распределение плотности частиц:
, t) – есть дифференциальная плотность частиц или пространственно-угловое и энергетическое распределение плотности частиц:
|
|
|
n (  , E,
, E,  , t )= dN / dV dE dΩ (2.1).
, t )= dN / dV dE dΩ (2.1).
Таким образом, дифференциальная плотность частицn (  , E,
, E,  , t ) – число частиц или фотонов, находящихся в момент времени t в единичном объеме, характеризуемом в пространстве вектором
, t ) – число частиц или фотонов, находящихся в момент времени t в единичном объеме, характеризуемом в пространстве вектором  , с кинетической энергией Е на единичный интервал энергий, движущихся в направлении
, с кинетической энергией Е на единичный интервал энергий, движущихся в направлении  в единичный телесный угол. Единицей измерения дифференциальной плотности частиц и системе СИ - м-3 Дж-1 ср-1. В радиационной физике более часто используются единицы: см-3 эВ-1 ср- 1 или см-3 МэВ-1 ср-1.
в единичный телесный угол. Единицей измерения дифференциальной плотности частиц и системе СИ - м-3 Дж-1 ср-1. В радиационной физике более часто используются единицы: см-3 эВ-1 ср- 1 или см-3 МэВ-1 ср-1.
Дифференциальная плотность частиц используется в основном в реакторной физике; в дозиметрии и защите от излучений и во многих прикладных задачах в качестве дифференциальной характеристики поля используется дифференциальная плотность потока частиц или фотонов.
Дифференциальная плотность потока частиц φ (  , E,
, E,  , t) – число частиц или фотонов с энергией Е на единичный интервал энергий, движущихся в направлении
, t) – число частиц или фотонов с энергией Е на единичный интервал энергий, движущихся в направлении  в единичный телесный угол и пересекающих в момент времени t за единицу времени помещенную в точке
в единичный телесный угол и пересекающих в момент времени t за единицу времени помещенную в точке  площадку единичной площади, нормаль к которой совпадает с направлением
площадку единичной площади, нормаль к которой совпадает с направлением  . Единицей измерения дифференциальной плотности потока частиц и системе СИ –
. Единицей измерения дифференциальной плотности потока частиц и системе СИ –
|
|
|
м-2 Дж-1 ср-1 с-1. В радиационной физике более часто используются единицы: см-2эВ-1 ср-1с-1 или см-2 МэВ-1 ср-1с-1.
Очевидна связь между введенными дифференциальными плотностью частиц и плотностью потока частиц, так как из частиц с энергией Е в единицу времени пересекут единичную площадку, расположенную перпендикулярно вектору  , лишь те, скорость которых равна v=
, лишь те, скорость которых равна v= 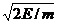 , где m- масса частицы:
, где m- масса частицы:
φ (  , E,
, E,  , t )= v n (
, t )= v n (  , E,
, E,  , t ) (2.2).
, t ) (2.2).
Для определения энергетических характеристик поля излучения вводится дифференциальная плотность потока энергии частиц или фотонов, связанная с плотностью потока частиц соотношением:
J (  , E,
, E,  , t )=E φ (
, t )=E φ (  , E,
, E,  , t ) (2.3).
, t ) (2.3).
Дифференциальные характеристики полей излучений в общем случае являются функциями 7 переменных: трех пространственных координат (x,y,z) или (r,θ,φ); двух угловых переменных (θ,φ), энергии частицы Е и времени t. В случае стационарных по времени задач, наиболее часто решаемых в физике защиты, дозиметрии и радиационной безопасности, временная зависимость не рассматривается и тогда введенные дифференциальные характеристики не зависят от времени t. В дальнейшем будем рассматривать характеристики стационарных полей излучений.
|
|
|
Наряду с дифференциальными характеристиками поля для решения многих практических задач достаточно знания интегральных характеристик, в частности:
пространственно-энергетического распределения плотности потока частиц:
φ (  , E )= ∫ φ (
, E )= ∫ φ (  , E,
, E,  ) d Ω (2.4),
) d Ω (2.4),
либо пространственно-углового распределения плотности потока частиц:
φ (  ,
,  )= ∫ φ (
)= ∫ φ (  , E,
, E,  ) d Е (2.5).
) d Е (2.5).
Наиболее интегральной и часто используемой величиной является пространственное распределение плотности потока частиц, часто называемое просто плотность потока частиц:
φ (  )= ∫ ∫ φ (
)= ∫ ∫ φ (  , E,
, E,  ) d Ω d Е (2.6).
) d Ω d Е (2.6).
Ее единицей в системе СИ является м-2 с-1, предпочтительней - см-2 с-1.
При интегрировании по энергии и углам дифференциальной плотности потока энергии частиц или фотонов получаем пространственное распределение плотности потока энергии или плотность потока энергии частиц, которую часто называют интенсивностью излучения:
J (  )= ∫ ∫ J (
)= ∫ ∫ J (  , E,
, E,  ) dΩ dЕ = ∫ ∫ E φ (
) dΩ dЕ = ∫ ∫ E φ (  , E,
, E,  ) dΩ dЕ (2.7).
) dΩ dЕ (2.7).
Определим физический смысл плотности потока частиц на примере ее определения в некоторой точке пространства, характеризуемой вектором  , на основе понятия элементарной сферы. Пусть dN1 - число частиц, пересекающих элементарную дисковую площадку dS1, центр которой расположен в точке
, на основе понятия элементарной сферы. Пусть dN1 - число частиц, пересекающих элементарную дисковую площадку dS1, центр которой расположен в точке  , перпендикулярную вектору
, перпендикулярную вектору  1, и летящих в телесный угол ΔΩ1 (рис.2.2). Тогда пространственно – угловое распределение плотности потока частиц в точке
1, и летящих в телесный угол ΔΩ1 (рис.2.2). Тогда пространственно – угловое распределение плотности потока частиц в точке  , летящих в этом направлении будет равно
, летящих в этом направлении будет равно
|
|
|
φ1 (  ,
,  1) = dN1 / dS1 ΔΩ1.
1) = dN1 / dS1 ΔΩ1.
 Рис.2.2. К определению плотности потока частиц.
Рис.2.2. К определению плотности потока частиц.
Из аналогичных рассуждений пространственно-угловое распределение плотности потока частиц в точке  , летящих в направлении
, летящих в направлении  2 будет равно φ2 (
2 будет равно φ2 (  ,
,  2) = dN2 / dS2 ΔΩ2, летящих в направлении
2) = dN2 / dS2 ΔΩ2, летящих в направлении  3 будет равна φ3 (
3 будет равна φ3 (  ,
,  3) = dN3 / dS3 ΔΩ3 и т.д. Следует отметить, что при определении дифференциальной или интегральной плотности потока частиц площадка dS всегда должна быть направлена перпендикулярно направлению
3) = dN3 / dS3 ΔΩ3 и т.д. Следует отметить, что при определении дифференциальной или интегральной плотности потока частиц площадка dS всегда должна быть направлена перпендикулярно направлению  движения частиц.
движения частиц.
Плотность потока частиц в точке  по определению равна:
по определению равна:
Φ (  )=∫ φ(
)=∫ φ(  ,
,  )dΩ =
)dΩ = 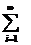 φi (
φi (  ,
,  i) ΔΩi =
i) ΔΩi =
= 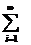 dN1 /dS1+dN2/dS2+dN3/dS3+...+dNк/dSк+..
dN1 /dS1+dN2/dS2+dN3/dS3+...+dNк/dSк+..
Учитывая, что dS1=dS2=dS3= dSк=dS, получаем
φ (  )=
)= 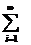 (dN1+ dN2+ dN3+.. dNк+..) / dS=
(dN1+ dN2+ dN3+.. dNк+..) / dS= 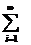 dNi / dS .
dNi / dS .
Таким образом, плотность потока частиц можно определить как число частиц, проникающих в объем расположенной в точке  элементарной сферы, отнесенное к площади поперечного сечения этой сферы. Следовательно, если в поле излучения ввести сферический невозмущающий это поле детектор, имеющий независимую от энергии и направления полета частиц чувствительность, то он будет регистрировать плотность потока частиц.
элементарной сферы, отнесенное к площади поперечного сечения этой сферы. Следовательно, если в поле излучения ввести сферический невозмущающий это поле детектор, имеющий независимую от энергии и направления полета частиц чувствительность, то он будет регистрировать плотность потока частиц.
В некоторых задачах радиационной безопасности, например, при изучении радиационной стойкости материалов в мощных полях ионизирующих излучений, особенно в случае изменения их характеристик со временем, используется понятие флюенс частиц, как интеграл по некоторому временному промежутку от Т1 до Т2 от плотности потока частиц:
Φ (  ) =
) = 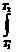 φ (
φ (  , t) dt (2.8).
, t) dt (2.8).
Единицей флюенса частиц в системе СИ является м-2, более часто используется см-2.
Введенные дифференциальные и интегральные характеристики полей излучений являются скалярными величинами и называются потоковыми.
Наряду с ними существует большой класс токовыххарактеристик полей излучений.
Дата добавления: 2018-05-13; просмотров: 875; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
