Краткие теоретические сведения

Показателями надежности восстанавливаемой АИС являются:

1) К_г(t)- функция готовности;

2) К_г- коэффициент готовности;

3) Т - среднее время между отказами в обслуживании (наработка на отказ).

Функционирование восстанавливаемой АИС можно описать с помощью структурной схемы функционирования резервированной системы с замещением кратности mпри числе обслуживающего персонала n=m.

Структурная схема и граф состояний системы изображены на рис. 8.1 и 8.2 соответственно.

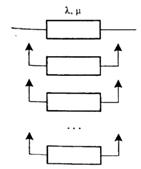
Рис. 8.1. Структурная схема системы

Рис. 8.2. Граф состояний системы

В состоянии nвсе каналы обслуживания заняты и очередной заявке будет отказано в обслуживании. Тогда p_n(t) - вероятность отказа системы, а (1-p_n(t)) - функция готовности. Коэффициент готовности определяется по формуле:

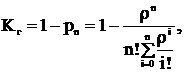
где .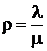

Отсюда следует, что определение числа обслуживающего персонала сводится к решению трансцендентного уравнения при различных значениях К_г и r.

Представим уравнение для коэффициента простоя в следующем виде:

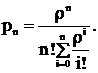(8.1)

Лабораторные задания и методические указания по их выполнению

Первое лабораторное задание

Определить количество обсуживающего персонала n, обеспечивающего заданное значение P.

Пример выполнения задания

Пусть интенсивность потока заявок l=5,1 час^-1, интенсивность обслуживания заявки µ=1,5 час^-1. Определим количество обслуживающего персонала, обеспечивающего К_г=0,8; 0,9; 0,95; 0,997.

В строках #1-#2файла в системе Deriveзададим составляющие трансцендентного уравнения (8.1), в строке #3- сумму выражения #2 (кнопка FindSum). В строке #4 записано конечное уравнение, полученное путем ввода выражения p=#1/#3 (рис. 8.3). В строке #5 приведено трансцендентное уравнение, полученное в результате подстановки в уравнение (8.1) численных значений исходных данных r=l/µ=5,1/1,5=3,4 и p=0,2 (p=1-К_г=1-0,8=0,2) с помощью кнопки VariableSubstitution.

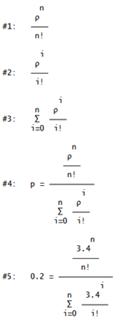
Рис. 8.3. Получение трансцендентного уравнения

В строках #6 и #7 (рис. 8.4) происходит вызов функции NSOLVE решения алгебраических уравнений численным методом и показан результат решения для p=0,2 соответственно.

Рис. 8.4.Решение алгебраических уравнений численным методом

Аналогично в строках #8-#16 (рис. 8.5-8.6) осуществляется решение алгебраических уравнений численным методом и показаны результаты для p=0,1; 0,05; 0,003.

Рис. 8.5. Решение алгебраических уравнений численным методом для p=0,1 и p=0,05

Рис. 8.6. Решение алгебраических уравнений численным методом для p=0,003.

Сведем полученные результаты в таблицу, округляя значение n до ближайшего целого в сторону увеличения.

Таблица 8.1

Результаты определения числа обслуживающего персонала

К_г	0,8	0,9	0,95	0,997
n	5	6	7	10

Полученные результаты будут иметь смысл лишь в том случае, если длительность переходных процессов мала. В противном случае результаты могут быть существенно завышены.

Второе лабораторное задание

Определить длительность переходных процессов в восстанавливаемой АИС.

Пример выполнения задания

Исследуем длительность переходных процессов на основании анализа функции готовности К_г(t). В строке #17 происходит настройка системы на ввод переменных с индексами (рис. 8.7). В строках #18-#20 задается система дифференциальных уравнений, в строке #21 происходит вызов утилиты для решения систем дифференциальных уравнений. В строке #22 вызывается функция RK([#18,#19,#20], [t,p0,p1,p2], [0,1,0,0], 0.1, 50) для решения системы дифференциальных уравнений методом Рунге-Кутты с шагом 0,1 и числом точек, равным 50. Затем в строке #23 осуществляется подстановка значений l=5,1 час^-1 и µ=1,5 час^-1, задаются начальные условия p₀(0)=1,p₁(0)=p₂(0)=0 (VariableSubstitution) и производится расчет (кнопка Approximate).

Результаты решения системы уравнений приведены в строке #24 (на рис. 8.8 показаны результаты в диапазоне t=1,7-2,7).

Рис.8.7. Исследование длительности переходных процессов на основании анализа функции готовности К_г(t)

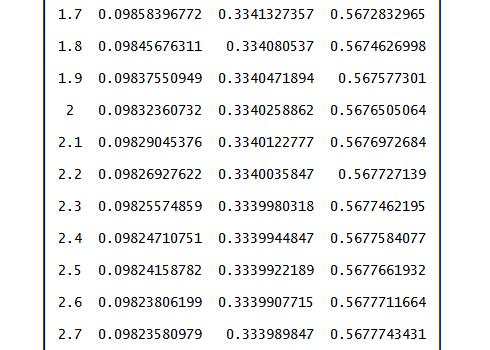
Рис.8.8. Результаты решения системы уравнений

Из рис.8.8 видно, что длительность переходного процесса составляет примерно 2,4 часа, вычисленного с точностью до четвертого знака после запятой. Так как длительность переходных процессов мала, то данные таблицы 8.1 можно считать достоверными.

Третье лабораторное задание

Определить функцию готовности восстанавливаемой АИС.

Пример выполнения задания

Вычислим функцию готовности, воспользовавшись выражением К_г(t)=1-p_n(t). Для получения решения в аналитическом виде воспользуемся преобразованием Лапласа (рис. 8.9).

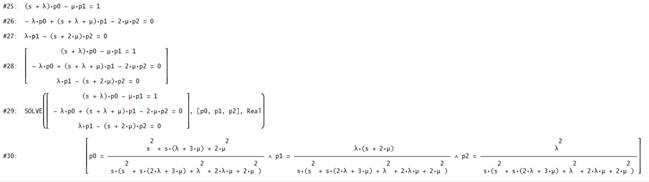
Рис. 8.9. Вычисление функции готовности

В строках #25-#27 представлены уравнения в преобразованиях Лапласа. В строке #28отображается система уравнений, полученная после нажатия кнопки AuthorMatrix. Решение системы получено с помощью функции SOLVE (строка #29) и представлено в строке #30 (кнопка Approximate).

Из общего решения выделено выражение для преобразования Лапласа коэффициента простоя p₂(s) (рис. 8.10). В строке #32 выполнена подстановка значений с помощью кнопки Sub. Результат расчета показан в строке #33.

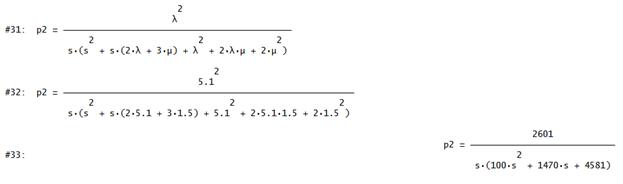
Рис. 8.10. Выражение для коэффициента простоя p₂(s)

С помощью математической системы MathCAD получим выражение для функции простоя путем обратного преобразования Лапласа (рис.8.11), затем построим графики функций простоя и готовности системы.

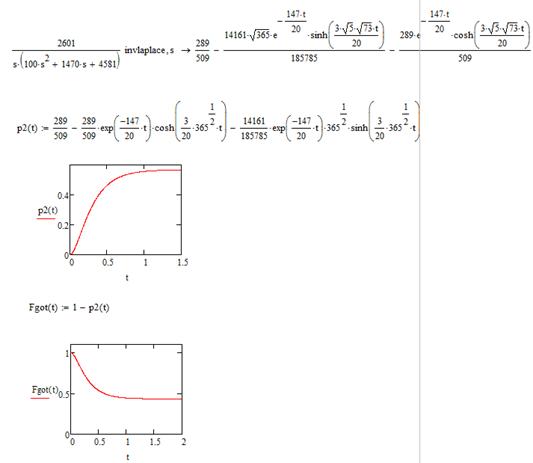
Рис. 8.11. Графики функций простоя и готовности системы

Дата добавления: 2018-05-12; просмотров: 216; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 11 12 13 14 15 161718 19 20 Следующая ⇒

Мы поможем в написании ваших работ!