Перевод чисел из двоичной системы счисления в десятичную
Пример 2.2.1Перевести ранее найденные двоичные числа 1011112 (4710) и 0,010001112 (0,2810), а также 101011,11111012 (43,97810) в десятичные.
Решение. Пронумеруем разряды числа справа налево, начиная с нулевого. Вычислим сумму произведений степеней основания системы счисления и цифр числа. Получим:
1·25 + 0·24 + 1·23 + 1·22 + 1·21 + 1·20 = 32 + 8 + 4 + 2 + 1 = 4710
0,010001112 = 0·2-1 + 1·2-2 + 0·2-3 + 0·2-4 + 0·2-5 + 1·2-6 + 1·2-7 + 1·2-8 = 0,25 + 0,015625 +
+ 0,0078125 + 0,00390625 = 0,277310
101011,11111012 = 1·25 + 0·24 + 1·23 + 0·22 + 1·21 + 1·20 + 1·2-1 + 1·2-2 + 1·2-3 + 1·2-4 + 1·2-5 + 0·2-6 +
+1 2-7= 32 + 8 + 2 + 1 +  = 4310
= 4310
Представление в компьютере отрицательных чисел
Пример 2.3.1Возьмите первое исходное число (4) со знаком минус: -46 и представьте его в форме значения со знаком и в форме обратного дополнительного кода.
Решение. Форма значения со знаком:старший (левый) разряд отмечается как знаковый и содержит информацию о знаке числа. Остальные разряды отводятся под абсолютную величину числа.
1 – число отрицательное: –4610 = 1010 11102;
0 – число положительное: 4610 = 0010 11102.
Форма обратного дополнительного кода.Перевод производится по следующему алгоритму:
- инвертировать все разряды числа, кроме знакового разряда;
- прибавить единицу к полученному коду;
- восстановить единицу в знаковом разряде.
Таким образом, преобразование заданного числа:
-4610 = 1010 11102 = 101 0001+1 = 101 0010 = 1101 00102.
Основные свойства дополнительного кода:
- Дополнительный код положительного числа – само число.
- Преобразование дополнительного кода по приведенному алгоритму перевода приводит к первоначальному виду числа в знаковой форме.
Арифметические операции в двоичной системе счисления
Пример 2.4.1Возьмем первое (46) и второе (91) исходные числа, записанные в двоичной системе счисления и вычислим их сумму.
Решение.Операция сложения выполняется так же, как и в десятичной системе.
Заметим, что при двоичном сложении 1+1 возникает перенос единицы в старший разряд, как в десятичной арифметике: 0+0=0, 0+1=1, 1+1=10.
Найдем сумму исходных чисел:
| + |
1 0 1 1 0 1 1 (9110)
1 0 0 0 1 0 0 1 (13710)
Пример 2.4.2 Возьмем первое (46) и второе (91) исходные числа, записанные в десятичной системе счисления и уменьшим их в m-раз, округлив до целого, так чтобы они находились в диапазоне от [5,20].
46/3 = 15,3 ≈ 15,
91/5 = 18,2 ≈ 18.
Переведем эти числа в двоичную систему счисления, и вычислим их произведение.
Решение.Правила умножения: 0∙0=0, 0∙1=0, 1∙0=0, 1∙1=1. Умножение двоичных чисел производится в столбик, аналогично умножению десятичных чисел, которое сводится к серии повторных сложений. Если цифра в нулевой позиции множителя равна 1, то множимое переписывается под соответствующими разрядами, умножение на последующие единицы приводит к сдвигу слагаемого влево на одну позицию. Если цифра множителя равна 0, то следующее слагаемое смещается на две позиции влево.

Ответ: 1510 ∙ 1810 = 27010 = 1 0000 11102;
1 0000 11102 = 1∙28 + 1∙23 + 1∙22 + 1∙21 = 256 + 8 + 4 + 2 = 27010
Пример 2.4.3 Возьмем первое (46) и второе (91) исходные числа, записанные в десятичной системе счисления. Переведем эти числа в двоичную систему счисления, и вычислим их разность.
Решение.Правила вычитания: 0-0=0, 1-0=1, 1-1=0, 10-1=1 (единица берется из старшего разряда). Операцию вычитания будем заменять операцией сложения:
91 – 46 = 91 + (-46).
Правила вычитания в двоичной системе:Алгоритм операции вычитания путем сложения дополнительных кодов:
1) преобразовать отрицательное число из формы со знаком в дополнительный код;
2) выполнить операцию двоичного сложения над всеми разрядами, включая знаковый, игнорируя единицу переноса из самого высокого разряда;
3) при равенстве единице знакового разряда суммы, что означает получение отрицательного результата в форме дополнительного кода, необходимо перевести результат в знаковую форму, используя второе свойство дополнений.
46 – 91 = 46 + (-91)
1) -9110 = 11 011 011 = 0 100 100 + 1 = 0 100 101 = 10 100 101
| 2) |
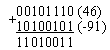
3) 11 010 011 = 0 101 100 + 1 = 10 101 101 = -4510
Пример 2.4.4 Возьмем первое (46) и второе (91) исходные числа, записанные в десятичной системе счисления. Переведем эти числа в двоичную систему счисления, и вычислим их разность.
Решение.91-46 = 91 + (-46)
1) -4610 = 10101110 = 10101110 + 1 = 1010010 = 11010010
| 2) |
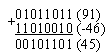
Пример 2.4.5Выполнить деление числа 27010 на 1510 (или в двоичной системе счисления 1 0000 11102 на 11112).
Решение.При выполнении операции деления несколько раз производится операция вычитания. Поэтому предварительно следует найти дополнительный код делителя. Дополнительный код числа 1111→11110001. Деление выполняется путем повторного вычитания и сдвига. Поскольку по правилам деления каждое промежуточное делимое должно быть больше делителя, выбираем в качестве первого делимого число 1000, т.е. первые пять разрядов добавляем слева три нуля, дополняя делимое до 8 разрядов. Затем производится его сложение с дополнительным кодом делимого и заносится в результат единица. Если следующее делимое после сноса очередной цифры будет меньше делителя, то в результат заносится нуль и в делимое сносится еще одна цифра из исходного делимого.

Ответ: 000100102 = 1810
Дата добавления: 2018-05-12; просмотров: 855; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
