Перевод чисел из десятичной системы счисления в двоичную
Для перевода целых чисел из десятичной системы счисления в двоичную чаще всего применяют два метода: метод поэтапного деления на основание системы счисления и метод разностей.
Пример 2.1.1 Перевод целого десятичного числа.
1 способ.
Получите запись числа2023 (9) (в двоичной с.с. 11111100111) и числа1964(7) (в двоичной с.с. 1110101100) в соответствие с примером перевода первого числа 2023 показанного на рисунке 2.1. Проверьте правильность перевода, используя программу калькулятор (Пуск – Программы – Стандартные – Калькулятор).
2-способ.
Найдите запись исходного десятичного числа 47 – двух последних цифр номера зачетной книжки в двоичной системе счисления.
Решение.Воспользуемся методом поэтапного деления.
Метод поэтапного делениязаключается в последовательном выполнении следующих действий:
1. Исходное число делим на основание системы счисления с остатком в десятичной с.с.
2. Если частное от деления не равно 0, выполняем п.1.
3. Полученные остатки записываем последовательно от последнего к первому.
4. Полученная запись – искомое двоичное число.
То есть, для того, чтобы перевести десятичное число в двоичную систему счисления, делим его на 2 «уголком» и выписываем получившиеся остатки в обратном порядке.
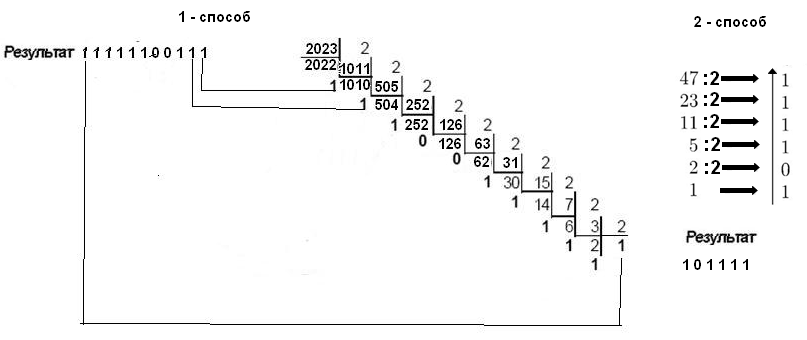
Рисунок 1 – Перевод десятичного числа в двоичную систему счисления
Пример 2.1.2Перевод десятичной дроби. Перевести пятое число 0,28 (8) в двоичную систему счисления с точностью до 10–8.
|
|
|
Решение.Воспользуемся правилом перевода десятичной дроби в двоичную систему.
0,28 × 2 = 0,56. Первая цифра двоичного числа после запятой – 0.
0,56 × 2 = 1,12. Вторая цифра двоичного числа – 1. Оставляем дробную часть: 0,12.
0,12 × 2 = 0,24. Третья цифра двоичного числа – 0.
0,24 × 2 = 0,48. Четвертая цифра двоичного числа – 0.
0,48 × 2 = 0,96. Пятая цифра двоичного числа – 0.
0,96 × 2 = 1,92 Шестая цифра двоичного числа – 1. Оставляем дробную часть: 0,92.
0,92 × 2 = 1,84. Седьмая цифра двоичного числа – 1. Оставляем дробную часть; 0,84.
0,84 × 2 = 1,68. Восьмая цифра двоичного числа – 1. Оставляем дробную часть: 0,68.
Требуемая точность достигнута.
Следовательно, 0,2810 = 0,010001112 с точностью до 10–8.
Пример 2.3.Перевод смешанных десятичных чисел. Перевести шестое число 43,978 (9) в двоичную систему счисления с точностью до 10–8.
Решение.Чтобы перевести смешанное число в другую систему счисления, нужно отдельно перевести целую и дробную части, а затем полученные результаты записать соответственно слева и справа от запятой.
Перевод целой части: Перевести десятичное число 43 в двоичную систему счисления.
Метод разностей.Для перевода чисел этим методом нам понадобится таблица степеней числа 2 (таблица 2).
|
|
|
Таблица 2 – Степени числа 2
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 2n | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | 65536 |
Какие степени «2» представлены в этом числе?
1) Ищем по таблице степеней двойки самое большее число, меньшее 43. Это 32.
2) Вычитаем 43-32=11
3) Для числа 11 ищем по таблице самое большее число, меньшее 11. Это 8.
4) Вычитаем 11-8=3.
5) Ищем по таблице степеней двойки самое большее число, меньшее 3. Это 2.
6) Вычитаем 3-2=1.
7) Для числа 1 остался единственный вариант это степень 20 = 1.
Теперь можем записать разложение числа 43 по степеням «2»:
4310 =1*25 + 0*24 + 1*23 + 0*22 + 1*21 + 1*20 = 1010112
Обратите внимание: если целое двоичное число заканчивается на 0, то соответствующее ему десятичное число будет четным; если двоичное число заканчивается на 1, то соответствующее ему десятичное число будет нечетным.
Перевод дробной части: Перевести десятичную дробь 0,978 в двоичную систему счисления с точностью до седьмого двоичного знака.
0,978 × 2 = 1,956. Первая цифра двоичного числа после запятой – 1.
0,956 × 2 = 1,912. Вторая цифра двоичного числа – 1.
0,912 × 2 = 1,824. Третья цифра двоичного числа – 1.
0,824 × 2 = 1,648. Четвертая цифра двоичного числа – 1.
|
|
|
0,648 × 2 = 1,296. Пятая цифра двоичного числа – 1.
0,296 × 2 =0,592. Шестая цифра двоичного числа – 0.
0,592× 2 = 1,184. Седьмая цифра двоичного числа – 1.
Требуемая точность достигнута.
Следовательно, 0,97810 = 0,11111012 с точностью до 10–7.
Ответ: смешанное число 43,97810 = 101011,11111012.
Дата добавления: 2018-05-12; просмотров: 3088; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
