Таблицы истинности логических выражений
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.
Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.
Алгоритм построения таблицы истинности:
1) подсчитать количество переменных (n) в логическом выражении;
| (18) |
m = 2n,
где n – количество логических переменных.
3) подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице истинности, которое равно сумме количества переменных и количества логических операций;
4) написать названия столбцов таблицы истинности в соответствии с последовательностью выполнения логических операций (с учетом скобок и приоритетов);
5) заполнить столбцы входных переменных наборами значений;
6) провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.
Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю – единицами;
|
|
|
б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц, начиная с группы нулей;
в) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
Пример 4.5.1 Построим таблицу истинности для выражения 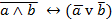 .
.
Решение. Количество строк в таблице истинности – 22 =4.
Количество столбцов: 2 + 6=8
Построим таблицу истинности. Названия столбцов – имена логических переменных и логические операции, расположенные с учетом их приоритета:
| a | b | 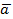
| 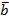
| 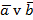
| a Ù b | 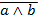
| 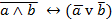
|
Начинаем заполнять таблицу истинности:
1. Заполним первый столбец. Делим столбец на 2, половину заполняем 0, половину 1, начиная с 0.
| a | b | 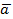
| 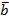
| 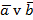
| a Ù b | 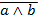
| 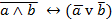
|
| 0 | |||||||
| 0 | |||||||
| 1 | |||||||
| 1 |
2. Второй столбец делим на четыре и заполняем, чередуя 0 и 1, начиная с 0.
|
|
|
| a | b | 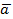
| 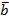
| 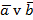
| a Ù b | 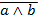
| 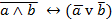
|
| 0 | 0 | ||||||
| 0 | 1 | ||||||
| 1 | 0 | ||||||
| 1 | 1 |
3. Для заполнения третьего столбца, выполняем инверсию к переменной а.
| a | b | 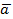
| 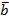
| 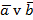
| a Ù b | 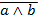
| 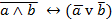
|
| 0 | 0 | 1 | |||||
| 0 | 1 | 1 | |||||
| 1 | 0 | 0 | |||||
| 1 | 1 | 0 |
4. Заполняем четвертый столбец, выполняя инверсию к переменной b.
| a | b | 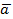
| 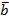
| 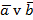
| a Ù b | 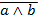
| 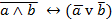
|
| 0 | 0 | 1 | 1 | ||||
| 0 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 1 | ||||
| 1 | 1 | 0 | 0 |
5. Все последующие столбцы, заполняем, выполняя логические операции:
| a | b | 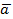
| 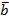
| 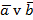
| a Ù b | 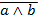
| 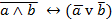
|
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
В последнем столбце таблицы получим значение функции. Как видно, при любых значениях входящих в нее логических переменных, её значение равно 1, то есть функция является тождественно-истинной.
|
|
|
Пример 4.5.2Какое из приведенных названий животных удовлетворяет логическому условию:
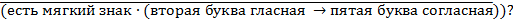
1) медведь 2) выхухоль 3) муравьед 4) обезьяна
Решение:рассмотрим порядок выполнения логических операций. В первую очередь будет выполняться действие в скобках (импликация), затем – конъюнкция и третье действие – инверсия (поскольку она задана для всего логического выражения). Таким образом, чтобы получить значение «истина», необходимо, чтобы после выполнения второго действия (конъюнкции) значение логического выражения было ложным.
Последовательно рассмотрим все возможные варианты:
1) Ответ 1: медведь.
Вторая буква гласная (1), пятая – гласная (0). Получаем: 1®0=0.
Есть мягкий знак – (1). Следовательно, 1∙0=0.
Выполнив инверсию, 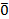 , получим 1.
, получим 1.
Ответ верный.
Рассмотрим оставшиеся варианты.
2) Ответ 2: выхухоль.
Вторая буква гласная (1), пятая – согласная (1). Получаем: 1®1=1.
Есть мягкий знак – (1). Следовательно, 1∙1=1.
Выполнив инверсию, 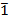 , получим 0.
, получим 0.
Ответ неверный.
3) Ответ 3: муравьед.
Вторая буква гласная (1), пятая – согласная (1). Получаем: 1®1=1.
Есть мягкий знак – (1). Следовательно, 1∙1=1.
Выполнив инверсию, 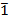 , получим 0.
, получим 0.
|
|
|
Ответ неверный.
4) Ответ 4: обезьяна.
Вторая буква согласная (0), пятая – не относится ни к какой из этих категорий, поэтому определить истинность логического высказывания не представляется возможным.
Ответ неверный.
На основании вышеизложенного, правильным является ответ 1 – медведь.
Попробуем решить эту задачу, используя таблицу истинности. Введем условные обозначения. Пусть
А – 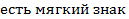 ;
;
B – 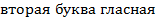
С – 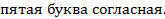
Запишем высказывание, используя обозначение логических операций:
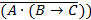
Построим таблицу истинности для каждого варианта ответа, с учетом приоритета логических операций:
| A | B | C | 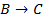
| 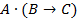
| 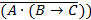
| |
| медведь | 1 | 1 | 0 | 0 | 0 | 1 |
| выхухоль | 1 | 1 | 1 | 1 | 1 | 0 |
| муравьед | 1 | 1 | 1 | 1 | 1 | 0 |
| обезьяна | 1 | 0 | – | – | – | – |
Как видно из таблицы истинности, правильным является первый ответ – медведь.
ЗАДАЧИ
1. Какое имя соответствует высказыванию:
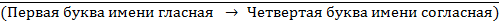 ?
?
1) ЕЛЕНА 2) ВАДИМ 3) АНТОН 4) ФЕДОР
2. Какое имя соответствует высказыванию:
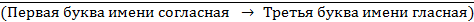 ?
?
1) ЮЛИЯ 2) ПЕТР 3) АЛЕКСЕЙ 4) КСЕНИЯ
3. Для какого символьного выражения неверно высказывание:
Первая буква гласная → 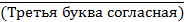 ?
?
1) abedc 2) becde 3) babas 4) abcab
4. Для какого символьного выражения верно высказывание:
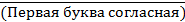 Ù
Ù 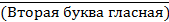 ?
?
1) abcde 2) bcade 3) babas 4) cabab
5. Для какого из указанных значений числа X истинно высказывание:
((X < 5)→(X < 3)) Ù ((X < 2)→(X < 1))?
1) 1 2) 2 3) 3 4) 4
6. Для какого из указанных значений числа X истинно высказывание:
((X > 3)Ú(X < 3)) →(X < 1)?
1) 1 2) 2 3) 3 4) 4
7. Для какого из указанных значений числа X истинно высказывание:
X > 1 Ù ((X < 5)→(X < 3))?
1) 1 2) 2 3) 3 4) 4
8. Для какого из указанных значений числа X истинно высказывание:
(X > 2)Ú(X > 5)→(X < 3)?
1) 5 2) 2 3) 3 4) 4
9. Для какого значения числа Z высказывание ((Z > 2)Ú(Z > 4)) →(Z > 3) будет ложным?
1) 1 2) 2 3) 3 4) 4
10. Для какого значения Y высказывание (Y<5)Ù((Y>1)→ (Y > 5)) будет истинным?
1) 1 2) 2 3) 3 4) 4
11. Укажите, какое логическое выражение равносильно выражению 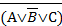 ?
?
1) 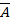 ÚBÚ
ÚBÚ 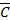 2) AÙ
2) AÙ 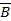 ÙC 3)
ÙC 3) 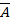 Ú
Ú 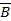 Ú
Ú 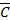 4)
4) 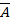 ÙBÙ
ÙBÙ 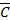
12. Укажите, какое логическое выражение равносильно выражению (AÙB)ÙC?
1) A Ú B Ú C 2) (A Ú B) Ù C 3) (A Ú B) Ù C 4) A Ù B Ù C
13. Укажите, какое логическое выражение равносильно выражению (А Ù B)?
1) A Ú B 2) A Ú B 3) B Ù A 4) A Ù B
14. Укажите, какое логическое выражение равносильно выражению (А Ú B)?
1) A Ú B 2) A Ù B 3) A Ú B 4) A Ù B
15. Укажите, какое логическое выражение эквивалентно выражению (A Ú B) Ù C?
1) (A Ú B) Ú C 2) A Ù B Ù C 3) (A → B)Ú C 4) (A Ú B)Ú C
16. Укажите, какое логическое выражение эквивалентно выражению A Ù (B Ù C)?
1) A Ù B Ù C 2) A Ú B Ú C 3) A Ù (B Ú C) 4) (A Ú B) Ù C
17. Укажите, какое логическое выражение эквивалентно выражению (A Ú B) Ù C?
1) (A Ú B) Ù C 2) (A Ù B) Ù C 3) (A Ù B) Ù C 4) (A Ú B) Ù C
18. Укажите, какое логическое выражение эквивалентно выражению (A Ú B) Ù C?
1) A Ú B Ù C 2) (A Ù B) Ù C 3) (A Ú C) Ú B 4) (A Ú C) Ù B
19. Укажите, какое логическое выражение эквивалентно выражению (A Ù B) Ù C?
1) (A Ù B) Ù C 2) (A Ú B) Ú C 3) (A Ù B) Ú C 4) (A Ú B) Ù C
20. Укажите, какое логическое выражение эквивалентно выражению (A Ú B) → C?
1) A Ù B Ù C 2) A Ú B Ú C 3) (A Ú B) Ú C 4) A Ú B Ú C
21. Укажите, при каких значениях переменных x и y ложно логическое выражение
не ((x ≤ 5) и (y <> 2)) и (x + y > 3)
1) x = 5, y = 2 2) x = 4, y = 1 3) x = 6, y = 2 4) x = 6, y = -2 5) x = 2, y = 2
22. Укажите, при каких значениях переменных x и y истинно логическое выражение
не ((x ≤ 5) и (y <> 2)) и (x + y > 3)
1) x = 4, y = 1 2) x = 1, y = -4 3) x = 6, y = 2 4) x = -1, y = 4 5) x = 5, y = 3
23. Укажите, при каких значениях переменных x и y истинно логическое выражение
(не (x ≤ 5) или (y = 2)) и не (x + y ≤ 3)
1). x = 6, y = 2 2). x = 4, y = 1 3). x = 1, y = -4 4). x = 5, y = 3 5). x = -1, y = 4
24. Укажите, при каких значениях переменных x и y ложно логическое выражение
(не (x ≤ 5) или (y = 2)) и не (x + y ≤ 3)
1) x = 5, y = 2 2) x = 2, y = 2 3) x = 6, y = 2 4) x = 4, y = 1 5) x = 6, y = -2
25. Укажите, при каких значениях переменных x и y ложно логическое выражение
не (x ≤ y + 2 - x) и не ((x + 2 > 4) и (x ≤ 2 – y))
1) x = 3, y = 1 2) x = 2, y = -2 3) x = 3, y = 3 4) x = 2, y = 0 5) x = 4, y = -2
26. Укажите, при каких значениях переменных x и y истинно логическое выражение
не (x > y + 2 - x) или не (x + 2 ≤ 4) и не (x > 2 – y)
1) x = 4, y = -2 2) x = 2, y = -2 3) x = 3, y = 1 4) x = 2, y = 0 5) x = 3, y = 3
27. Укажите, при каких значениях переменных x и y ложно логическое выражение
не ((y = x - 2) или не (x + y < 4 - x) и (2 * x – 3 * y ≥ 0))
1) x = 0, y = 0 2) x = 3, y = 2 3) x = 2, y = -1 4) x = -2, y = 1 5) x = -3, y = -1
28. Укажите, при каких значениях переменных x и y ложно логическое выражение
(y <> x - 2) и ((x + y < 4 - x) или не (2 * x – 3 * y ≥ 0))
1) x = -3, y = -1 2) x = 2, y = -1 3) x = 3, y = 2 4) x = -2, y = 1 5) x = 0, y = 0
29. Укажите, при каких значениях переменных x и y ложно логическое выражение
(x + 2 * y ≥ 3) и не (x +5 ≤ y) или (x < y - x)
1) x = -2, y = 2 2) x = 1, y = 3 3) x = 3, y = 2 4) x = -1, y = -2 5) x = 4, y = 2
30. Укажите, при каких значениях переменных x и y истинно логическое выражение
(не (x + 2 * y ≥ 3) или (x +5 ≤ y)) и (x ≥ y - x)
1) x = 1, y = 3 2) x = 3, y = 2 3) x = 4, y = 2 4) x = -2, y = 2 5) x = -1, y = -2
31. Сколько различных решений имеет уравнение
(K Ù L Ù M) Ú (L Ù M Ù N) = 1
где K, L, M, N – логические переменные?
В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.
32. Укажите значения переменных K, L, M, N, при которых логическое выражение
(K Ú M) → (L Ú M Ú N)
ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.
33. Корень X логического уравнения 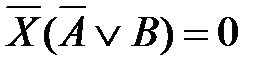 равен
равен
1) 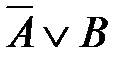 2)
2) 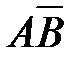 3)
3) 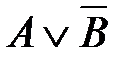 4)
4) 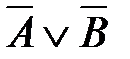 5)
5) 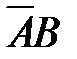
34. Корень X логического уравнения 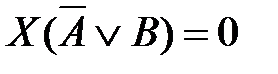 равен
равен
1) 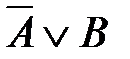 2)
2) 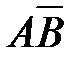 3)
3) 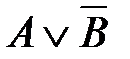 4)
4) 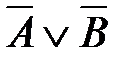 5)
5) 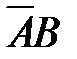
35. Корень X логического уравнения 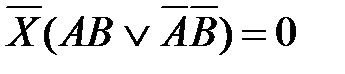 равен
равен
1) 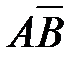 2)
2)  3)
3) 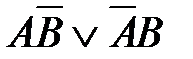 4)
4) 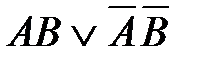 5)
5) 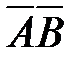
36. Корень X логического уравнения 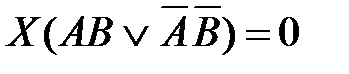 равен
равен
1) 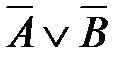 2)
2)  3)
3) 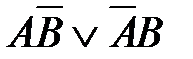 4)
4) 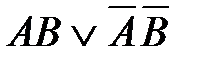 5)
5) 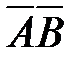
37. Корень X логического уравнения 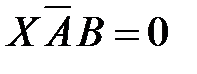 равен
равен
1) 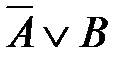 2)
2)  3)
3) 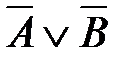 4)
4) 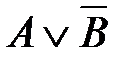 5)
5) 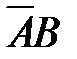
38. Корень X логического уравнения 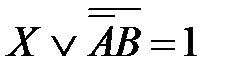 равен
равен
1) 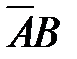 2)
2) 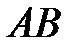 3)
3) 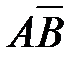 4)
4) 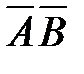 5)
5) 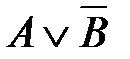
39. Корень X логического уравнения 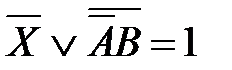 равен
равен
1) 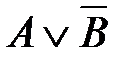 2)
2) 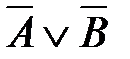 3)
3) 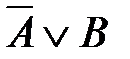 4)
4)  5)
5) 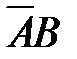
40. Корень X логического уравнения 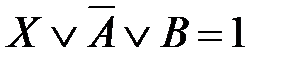 равен
равен
1) 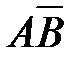 2)
2) 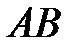 3)
3) 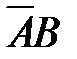 4)
4) 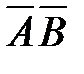 5)
5) 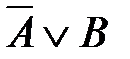
41. Корень X логического уравнения 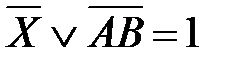 равен
равен
1) 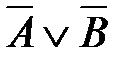 2)
2)  3)
3) 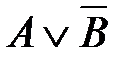 4)
4) 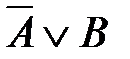 5)
5) 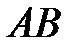
42. Корень X логического уравнения 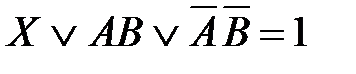 равен
равен
1) 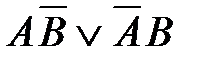 2)
2) 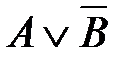 3)
3) 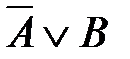 4)
4) 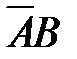 5)
5) 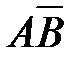
43. Упростите логические выражения:
1) 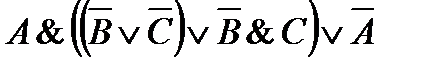
2) 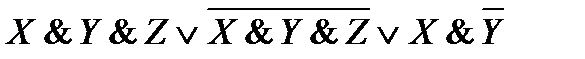
3) 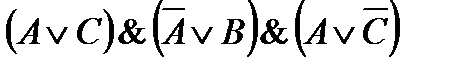
4) 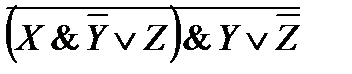
5) 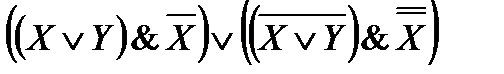
6) 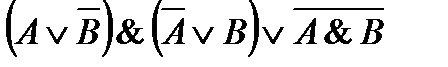
7) 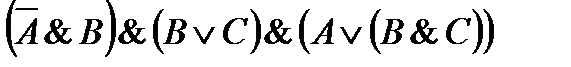
8) 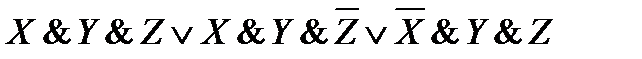
9) 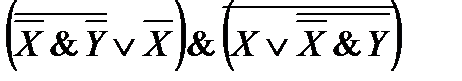
10) 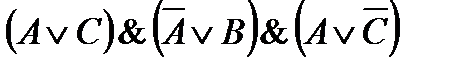
11) 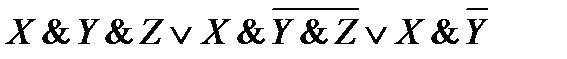
12) 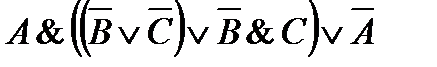
13) 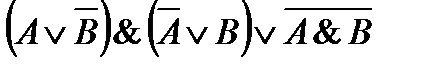
14) 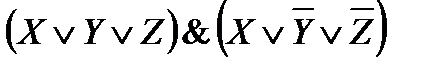
15) 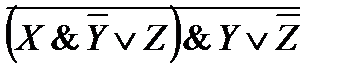
16) 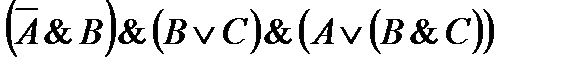
17) 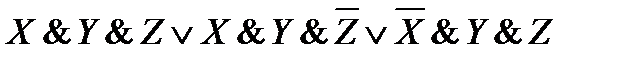
18) 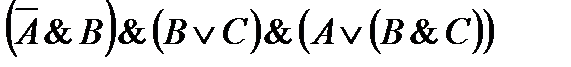
19) 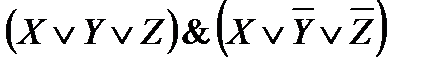
20) 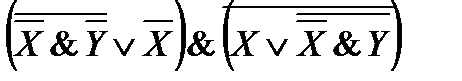
21) (A→ B & C) & (C→B & A) & (B→ C & A)
22) 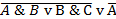
23) 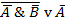
24) 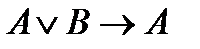
25) 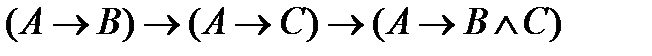
26) 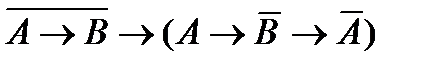
44. Установите, являются ли данные высказывания равносильными:
1) 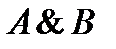 и
и 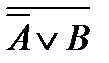
2) 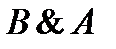 и
и 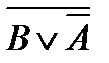
3) 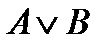 и
и 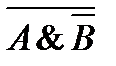
4) 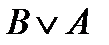 и
и 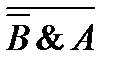
5) 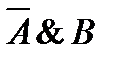 и
и 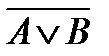
6) 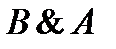 и
и 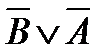
7) 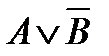 и
и 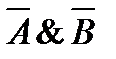
8) 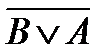 и
и 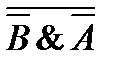
9) 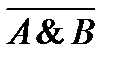 и
и 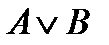
10) 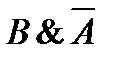 и
и 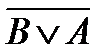
45. Постройте таблицу истинности логического выражения:
1) 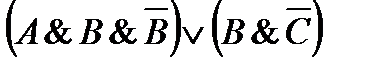 6)
6) 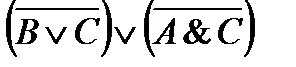
2) 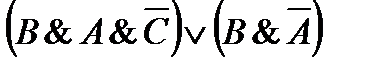 7)
7) 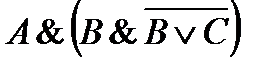
3) 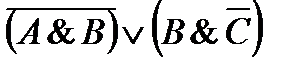 8)
8) 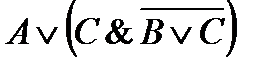
4) 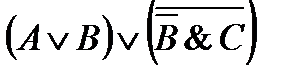 9)
9) 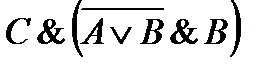
5) 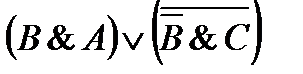 10)
10) 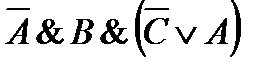
46. Укажите максимальное количество комбинаций значений логических переменных A, B и C при которых логическое выражение истинно:
1) 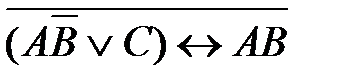 2)
2) 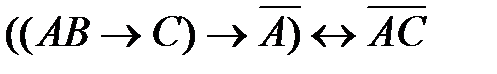 3)
3) 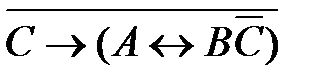
4) 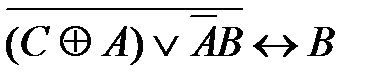 5)
5) 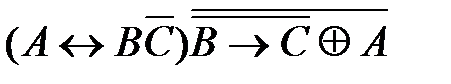
47. Укажите максимальное количество комбинаций логических переменных A, B и C при которых логическое выражение ложно:
1) 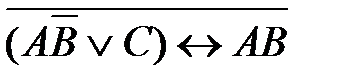 2)
2) 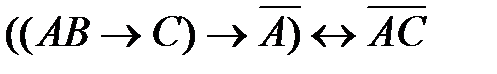 3)
3) 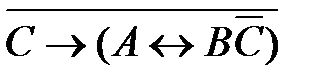
4) 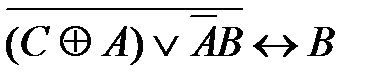 5)
5) 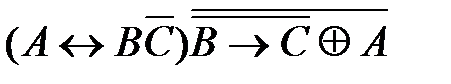
48. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 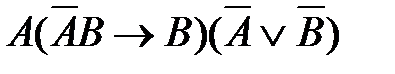 2)
2) 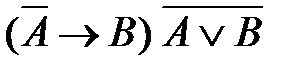 3)
3) 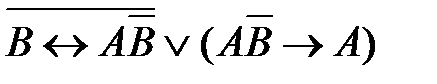
4) 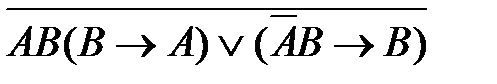 5)
5) 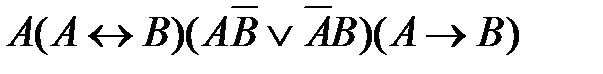
49. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 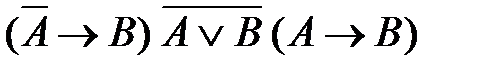 2)
2) 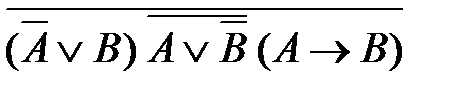
3) 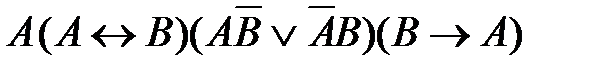 4)
4) 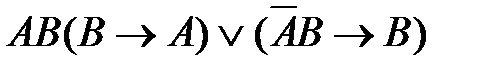
5) 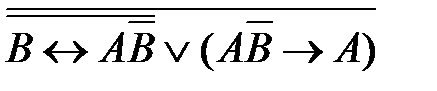
50. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 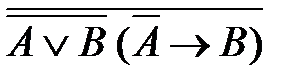 2)
2) 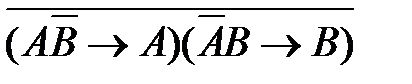 3)
3) 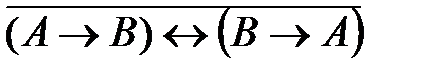
4) 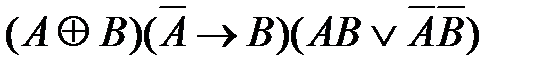 5)
5) 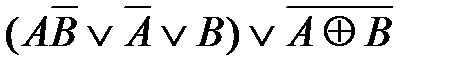
51. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 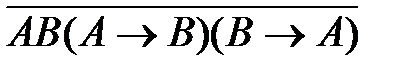 2)
2) 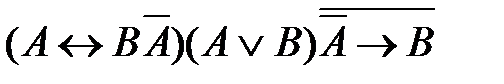
3) 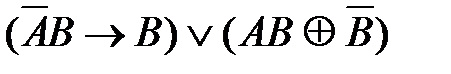 4)
4) 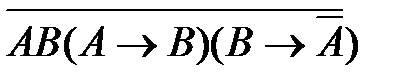
5) 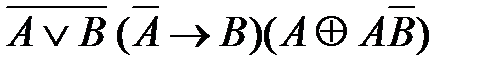
52. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 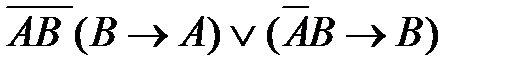 2)
2) 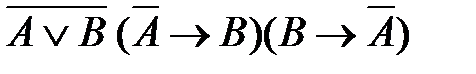 3)
3) 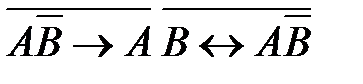
4) 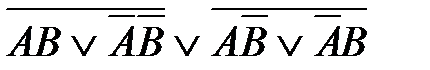 5)
5) 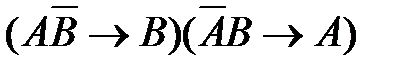
53. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 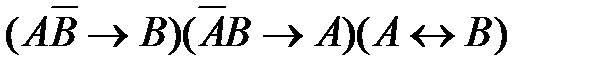 2)
2) 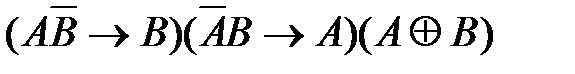
3) 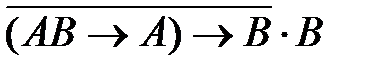 4)
4) 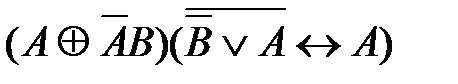 5)
5) 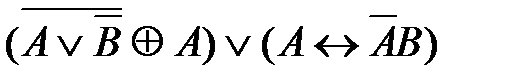
54. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 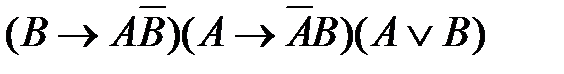 2)
2) 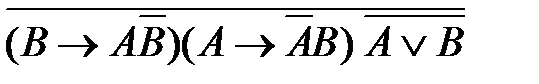
3) 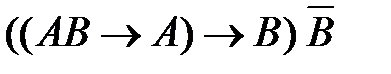 4)
4) 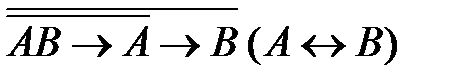
5) 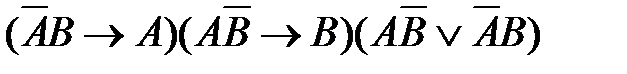
55. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 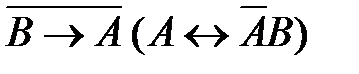 2)
2) 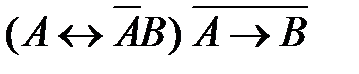 3)
3) 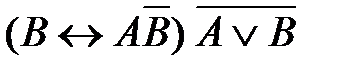
4) 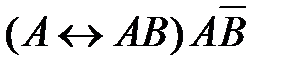 5)
5) 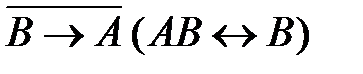
56. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 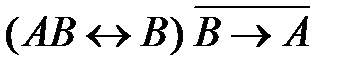 2)
2) 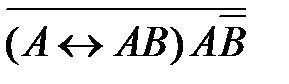 3)
3) 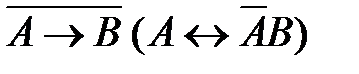
4) 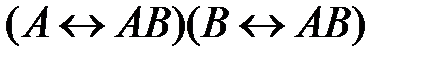 5)
5) 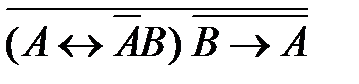
57. Укажите логическое выражение, которое не является ни тождественно истинным, ни тождественно ложным:
1) 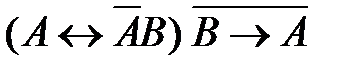 2)
2) 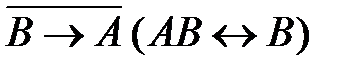 3)
3) 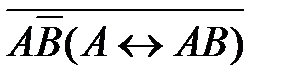
4) 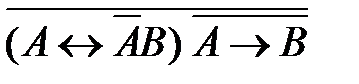 5)
5) 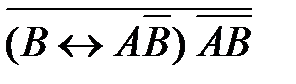
58. Данной таблице истинности:
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
соответствует логическая функция F(A,B,C):
1) 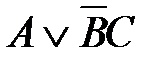 2)
2) 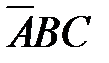 3)
3) 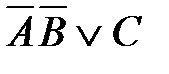 4)
4) 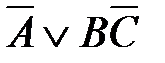 5)
5) 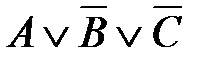
59. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
соответствует логическая функция F(A,B,C):
1) 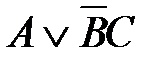 2)
2) 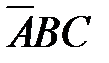 3)
3) 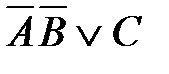 4)
4) 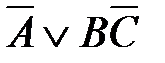 5)
5) 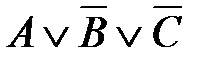
60. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
соответствует логическая функция F(A,B,C):
1) 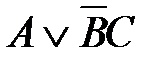 2)
2) 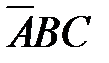 3)
3) 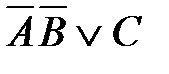 4)
4) 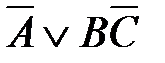 5)
5) 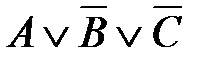
61. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
соответствует логическая функция F(A,B,C):
1) 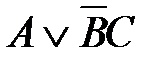 2)
2) 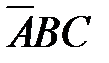 3)
3) 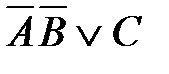 4)
4) 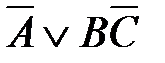 5)
5) 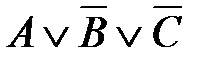
62. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
соответствует логическая функция F(A,B,C):
1) 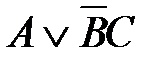 2)
2) 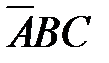 3)
3) 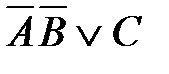 4)
4) 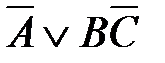 5)
5) 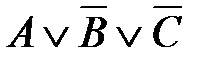
63. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
соответствует логическая функция F(A,B,C):
1) 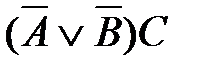 2)
2) 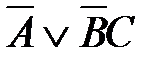 3)
3) 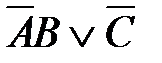 4)
4) 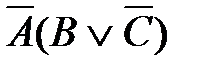 5)
5) 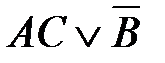
64. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
соответствует логическая функция F(A,B,C):
1) 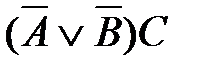 2)
2) 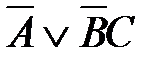 3)
3) 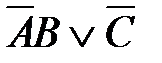 4)
4) 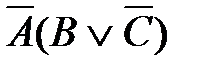 5)
5) 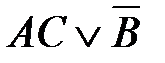
65. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
соответствует логическая функция F(A,B,C):
1) 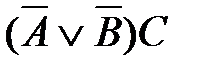 2)
2) 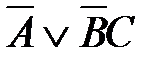 3)
3) 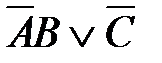 4)
4) 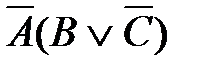 5)
5) 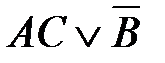
66. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
соответствует логическая функция F(A,B,C):
1) 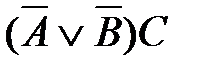 2)
2) 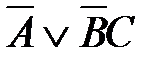 3)
3) 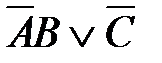 4)
4) 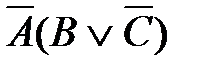 5)
5) 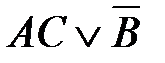
67. Данной таблице истинности
| A | B | C | F(A,B,C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
соответствует логическая функция F(A,B,C):
1) 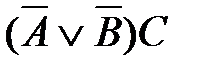 2)
2) 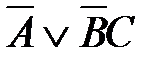 3)
3) 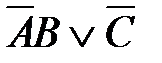 4)
4) 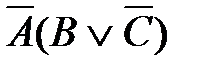 5)
5) 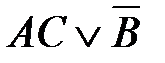
68. Корень X логического уравнения 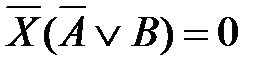 равен:
равен:
1) 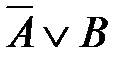 2)
2) 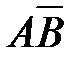 3)
3) 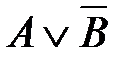 4)
4) 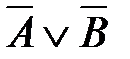 5)
5) 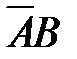
69. Корень X логического уравнения 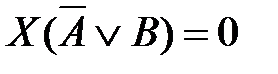 равен:
равен:
1) 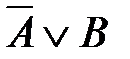 2)
2) 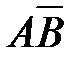 3)
3) 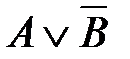 4)
4) 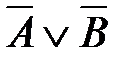 5)
5) 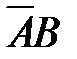
70. Корень X логического уравнения 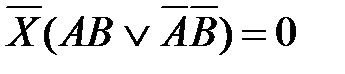 равен:
равен:
1) 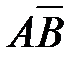 2)
2)  3)
3) 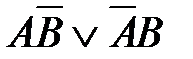 4)
4) 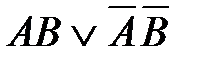 5)
5) 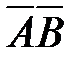
71. Корень X логического уравнения 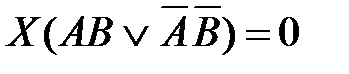 равен:
равен:
1) 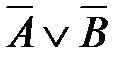 2)
2)  3)
3) 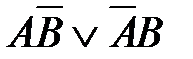 4)
4) 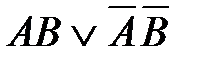 5)
5) 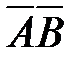
72. Корень X логического уравнения 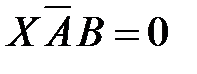 равен:
равен:
1) 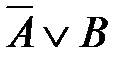 2)
2)  3)
3) 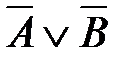 4)
4) 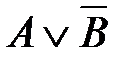 5)
5) 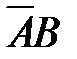
73. Корень X логического уравнения 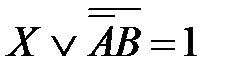 равен:
равен:
1) 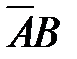 2)
2) 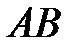 3)
3) 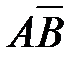 4)
4) 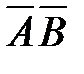 5)
5) 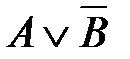
74. Корень X логического уравнения 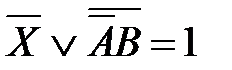 равен:
равен:
1) 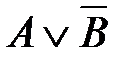 2)
2) 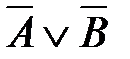 3)
3) 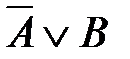 4)
4)  5)
5) 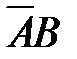
75. Корень X логического уравнения 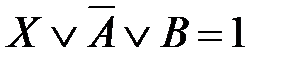 равен:
равен:
1) 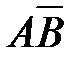 2)
2) 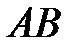 3)
3) 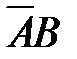 4)
4) 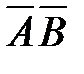 5)
5) 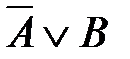
76. Корень X логического уравнения 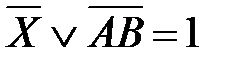 равен:
равен:
1) 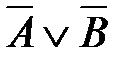 2)
2)  3)
3) 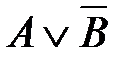 4)
4) 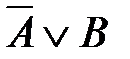 5)
5) 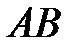
77. Корень X логического уравнения 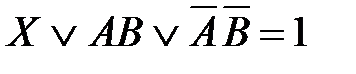 равен
равен
1) 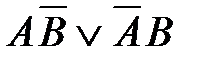 2)
2) 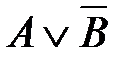 3)
3) 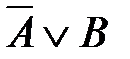 4)
4) 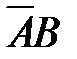 5)
5) 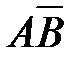
78. Укажите минимальное количество операций отрицания, конъюнкции и дизъюнкции с помощью которых можно вычислить логическую функцию F (A, B, C):
1) 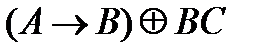 . 6)
. 6) 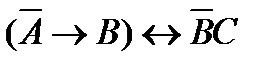
2) 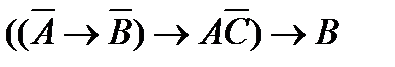 7)
7) 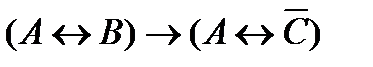
3) 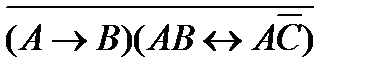 8)
8) 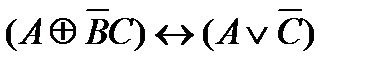
4) 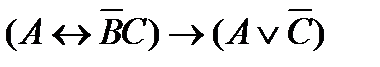 9)
9) 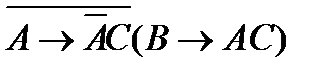
5) 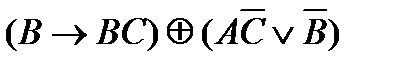 10)
10) 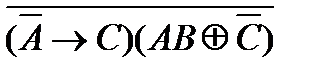
Дата добавления: 2018-05-12; просмотров: 2289; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
