Количество информации и вероятность
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ:
ТЕОРИЯ, УПРАЖНЕНИЯ, ЗАДАЧИ
Уфа 2012
Утверждено Редакционно-издательским советом УГНТУ
в качестве учебно - методического пособия
Каданцев М.Н., Михайловская И.М.
Представление информации: теория, упражнения, задачи: учебное методическое пособие. – Уфа: Изд-во УГНТУ, 2012. – 118 с.
Учебно-методическое пособие предназначено для студентов всех специальностей и форм обучения, изучающих курс информатики. Оно включает в себя описание различных форм представления информации, краткие теоретические сведения по соответствующим главам пособия, примеры и задачи.
Пособие состоит из 5 глав, соответствующих основным аспектам изучения разделов: измерение информации, системы счисления, кодирование информации, основы представления логической информации.
Приведена контрольная работа по системам счисления и кодированию информации.
Материалы пособия могут быть использованы для проведения практических занятий при изучении раздела «Теоретические основы информатики».
Для подготовки к занятиям рекомендуется использовать литературу из списка, приведенного в конце пособия и конспекты лекций.
| © Уфимский государственный нефтяной технический университет, 2012 | |
| © Каданцев М.Н., Михайловская И.М. |
Оглавление
|
|
|
Введение………………………………………………………………………….…..4
1. Измерение информации…………………………………………………………5
1.1. Содержательный подход………………………………………………….….5
1.2. Объемный подход…………………………………………………………….6
Задачи……………………………………………………………………….…8
1.3. Количество информации и вероятность…………………………………....10
Задачи………………………………………………………………………...15
2. Системы счисления…………………………………………………………….18
2.1. Перевод чисел из десятичной системы счисления в двоичную……….…19
2.2. Перевод числа из двоичной системы счисления в десятичную……….…22
2.3. Представление в компьютере отрицательных чисел………………….….22
2.4. Арифметические операции в двоичной системе счисления………….…..23
2.5. Восьмеричная и шестнадцатеричная системы счисления………………..25
3. Кодирование данных…………………………………………………………...27
3.1. Кодирование текстовой информации……………………………………..27
Задачи………………………………………………………………………..29
3.2. Кодирование графической информации………………………………….32
|
|
|
Задачи………………………………………………………………………..35
3.3. Кодирование звуковой информации………………………………………37
Задачи………………………………………………………………………..41
4. Основы логики………………………………………………………………….45
4.1. Высказывания……………………………………………………………….45
4.2. Алгебра логики……………………………………………………………...47
4.2.1. Логические операция ИНВЕРСИЯ………………………………..……….48
4.2.2 Логическая операция КОНЪЮНКЦИЯ…………………………………...49
4.2.3 Логическая операция ДИЗЪЮНКЦИЯ……………………………………50
4.2.4 Логическая операция ИСКЛЮЧАЮЩАЯ ДИЗЪЮНКЦИЯ……………50
4.2.5 Логическая операция ИМПЛИКАЦИЯ……………………………………51
4.2.6 Логическая операция ЭКВИВАЛЕНЦИЯ………………………………….52
Задачи…………………………………………………………………………………………………………..54
4.3. Логические формулы………………………………………………………………………………………….57
4.4. Упрощение логических формул……………………………………………………………………………...58
4.5 Таблицы истинности логических выражений……………………………………………………………….61
Задачи…………………………………………………………………………………………………………..65
4.6 Решение логических задач средствами алгебры логики…………………………………………………....76
|
|
|
4.6.1. Решение логических задач методом рассуждений………………………………………………………….76
4.6.2. Решение логических задач табличным методом………………………………………………………….....78
4.6.3. Решение логических задач с помощью логических выражений…………………………………………...81
Задачи…………………………………………………………………………………………………………..83
4.7. Алгебра логики и двоичное кодирование……………………………………………………………………92
4.7.1 Логические элементы компьютера…………………………………………………………………………...92
4.7.1.1 Схема И………………………………………………………………………………………………………...93
4.7.1.2 Схема ИЛИ...…………………………………………………………………………………………………...93
4.7.1.3 Схема НЕ…………………………………………………………………………………………………….....93
4.7.1.4 Схема И-НЕ…………………………………………………………………………………………………….94
4.7.1.5 Схема ИЛИ-НЕ………………………………………………………………………………………………...94
4.7.2. Переключательная схема……………………………………………………………………………………...94
Задачи…………………………………………………………………………………………………………100
5. Контрольная работа. Системы счисления. Кодирование данных………………………………………...103
|
|
|
5.1. Варианты заданий контрольной работы……………………………………………………………………104
Приложение А Таблицы сложения и умножения в позиционных системах счисления………………...113
Приложение Б Таблица символов ASCII…………………………………………………………………...114
Приложение В Таблицы символов CP866………………………………………………..………………...115
Список литературы……………………………………………………………………………………………………116
Введение
Человек участвует во множестве информационных процессов, которые он пытается в дальнейшем реализовать с помощью компьютерных технологий. Он способен:
- находить, различать и воспринимать естественную и искусственную информацию;
- анализировать, обобщать и классифицировать полученную информацию;
- накапливать и производить качественную и количественную информацию;
- трансформировать переработанную информацию в команды, управляющие предписания и целенаправленную последовательность действий.
Благодаря этим свойствам человек создает искусственную информацию и может выполнять определенные функции. Они лежат в основе разрабатываемых им вычислительных и информационных технологий, обеспечивающих в соответствующих системах реализацию вычислительных и информационных процессов. Наиболее значимыми считают такие информационные процессы, как получение, сбор, передача, преобразование, сохранение, обработка и использование информации. Во всех перечисленных информационных процессах используются различные формы представления информации, рассмотрению которых и посвящено данное методическое пособие.
Изучение курса информатики начинается с основ информационных процессов. В учебном пособии в доступной форме изложены основные темы по разделу теоретических основ курса информатики, которые сопровождаются примерами выполнения упражнений и задач, что, несомненно, должно облегчить процесс самостоятельного освоения материала.
Измерение информации
Определить понятие «количество информации» довольно сложно. В решении этой проблемы существуют два основных подхода. Исторически они возникли почти одновременно. В конце 40-х годов XX века один из основоположников кибернетики американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.
Содержательный подход
Количество информации, заключенное в сообщении, определяется объемом знаний, который несет это сообщение получающему его человеку. Сообщение содержит информацию для человека, если заключенные в нем сведения являются для этого человека новыми и понятными и, следовательно, пополняют его знания.
При содержательном подходе возможна качественная оценка информации: полезная, безразличная, важная, вредная... Одну и ту же информацию разные люди могут оценить по-разному, поэтому имеет место такой подход, как неизмеряемость информации в быту (информация как новизна для получателя).
Прежде, чем измерять значение какой-либо физической величины, надо ввести единицу измерения. У информации тоже есть такая единица – бит, но смысл ее различен при измерении информации в рамках разных подходов к определению понятия «информация».
Вы получили некоторое сообщение, например, прочитали статью в журнале. В этом сообщении содержится какое-то количество новых для Вас сведений. Как оценить, сколько информации Вы получили? Другими словами, как измерить информацию? Можно ли сказать, что чем больше статья, тем больше информации она содержит?
Разные люди, получившие одно и то же сообщение, по-разному оценивают его новизну и информационную емкость. Это происходит оттого, что знания людей о событиях, явлениях, о которых идет речь в сообщении, до получения сообщения были различными. Поэтому те, кто знал об этом мало, сочтут, что получили много информации, те же, кто знал больше, могут сказать, что информации не получили вовсе. Таким образом, количество информации в сообщении, зависит от того, насколько ново это сообщение для получателя.
Количество информации в одном и том же сообщении должно определяться отдельно для каждого получателя, т.е. иметь субъективный характер. Но субъективные вещи не поддаются сравнению и анализу, для их измерения трудно выбрать одну общую для всех единицу измерения. Поэтому, с точки зрения новизны, мы не можем однозначно и объективно оценить количество информации, содержащейся даже в простом сообщении. Что же тогда говорить об измерении количества информации, содержащейся в научном открытии, новом музыкальном стиле, новой теории общественного развития. Поэтому, когда информация рассматривается как новизна сообщения для получателя, вопрос об измерении количества информации не ставится.
Объемный подход
Объемный (алфавитный) подход к измерению информации позволяет определить количество информации, заключенной в тексте. Алфавитный подход является объективным, т.е. он не зависит от субъекта (человека), воспринимающего текст.
Он основан на подсчете числа символов в сообщении, т.е. связан только с длиной сообщения и не учитывает его содержания.
Длина сообщения зависит от числа знаков, употребляемых для записи сообщения. Например, слово «мир» в русском алфавите записывается тремя знаками, в английском – пятью (Peace), а в КОИ-8 (код обмена информацией 8 битный) – сорока битами.
Множество символов, используемых при записи текста, называется алфавитом. Количество символов алфавита называется мощностью (размером) алфавита.
Один символ алфавита мощностью 256 (28) несет в тексте 8 бит информации. Такое количество информации называется байт. Алфавит из 256 символов используется для представления текстов в компьютере: 1 байт = 8 бит.
В двоичной системе счисления знаки 0 и 1 будем называть битами. В компьютере бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе, определяется количеством требуемых для такой записи двоичных символов, целым количеством бит (в отличие от вероятностного подхода).
Для удобства использования введены более крупные, чем бит, единицы количества информации. Так, двоичное слово из восьми знаков содержит один байт информации. 1024 байта образуют килобайт (Кбайт), 1024 килобайта – мегабайт (Мбайт), а 1024 мегабайта – гигабайт (Гбайт).
Между вероятностным и объемным количеством информации неоднозначное соотношение. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускает его в объемном. Если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то это количество не обязательно совпадает, при этом кибернетическое количество информации не может быть больше объемного.
Пример 1.2.1 Книга, набранная с помощью компьютера, содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге?
Решение: Мощность компьютерного алфавита равна 256. Один символ несет 1 байт информации. Значит, страница содержит 40 х 60 = 2400 байт информации. Объем всей информации в книге (в разных единицах):
2 400 х 150 = 360 000 байт.
360 000/1024 = 351,5625 Кбайт.
351,5625/1024 = 0,34332275 Мбайт.
ЗАДАЧИ
1. Некоторыйалфавит состоит из 8 букв. Какое количество информации несет одна буква этого алфавита?
2. Сообщение, записанное буквами из 64-х символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
3. Информационное сообщение объемом 1,5 Кбайта содержит 3 072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
4. Объем сообщения, содержащего 2 048 символов, составил 1/512 часть Мбайта. Каков размер алфавита, с помощью которого записано сообщение?
5. Сколько символов содержит сообщение, записанное с помощью 16-ти символьного алфавита, если объем его составил 1/16 часть Мбайта?
6. Сколько килобайт в сообщении, содержащем 12 288 бит?
7. Сколько килобайт составит сообщение из 384 символов 16-ти символьного алфавита?
8. Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержат 5 страниц текста?
9. Сообщение нанимает 3 страницы по 25 строк. В каждой строке записано по 60 символов. Сколько символов в использованном алфавите, если все сообщение содержит 1125 байт?
10. Для записи сообщения использовался 64-х символьный алфавит. Каждая страница содержит 30 строк. Все сообщение содержит 8 775 байт информации и занимает 6 страниц. Сколько символов в строке?
11. Сообщение занимает 2 страницы и содержит 1/16 Кбайта информации. На каждой странице записано 256 символов. Какова мощность использованного алфавита?
12. Сколько двоичных разрядов потребуется для хранения и записи 1 бита, 5 бит, 16 бит?
13. ДНК человека можно представить как некоторое слово четырехбуквенного алфавита, где буквы соответствуют нуклеотидам. Определить, какое количество информации содержит ДНК, если она состоит примерно из 1,5×1023 нуклеотидов.
14. Сообщение, записанное буквами 64-символьного алфавита, содержит 20 символов. Какой объем информации оно содержит?
15. На книжном стеллаже 16 полок. Книга может быть поставлена на любую из них. Сколько информации содержит сообщение о том, где находится книга?
16. Страница книги состоит из 50 строк по 50 символов в строке. Чему равен информационный объем данной книги, если в ней 345 страниц (Ответ привести в Мб).
17. Сколько страниц машинописного текста (60 символов, 40 строк) содержится в текстовом файле объемом 500 Kб?
18. Подсчитайте информационный объем сообщения «Закончилась сессия!» (с точки зрения технического подхода, то есть, не учитывая смысл сообщения). Выразите этот объем в битах, байтах, килобайтах.
19. Для записи текста используются только строчные буквы русского алфавита и «пробел» для разделения слов. Какой информационный объем имеет текст, состоящий из 2 000 символов (одна печатная страница)?
20. Вычислить информационный объем текста размером в 2 000 символов, в записи которого использован алфавит компьютерного представления текстов мощностью 256.
21. Необходимо вычислить количество информации, содержащейся на одной странице набранного на компьютере текста. Текст состоит из 50 строк по 60 символов. Вычислить количество информации на 10 страницах.
22. Объем информационного сообщения 12 288 бит. Сколько это будет в байтах, Килобайтах, Мегабайтах?
23. Мощность некоторого алфавита равна 64 символам. Какой объем информации содержится в тексте, содержащем 100 символов?
24. Изображение на экране содержит 128 х 64 точек. Каждая точка может иметь один из 256 оттенков. Каков минимальный объем памяти, необходимый для хранения этого изображения?
25. Сообщение объемом информации 0,25 Кбайт содержит по 128 символов на каждой из 4 страниц. Чему равна мощность использованного алфавита?
26. Определить количество байт, переданных по каналу с пропускной способностью 100 Мбит/с за 4 секунды.
27. Сообщение занимает 3 страницы по 25 строк. Каждая строка содержит 60 знаков. Информационный объем сообщения – 1125 байт. Какое количество символов использовано для записи данного сообщения?
28. Какое количество информации, необходимо для кодирования оценок «неудовлетворительно», «удовлетворительно», «хорошо» и «отлично»?
29. Два сообщения содержат одинаковое количество символов. Количество информации в первом тексте в 1,5 раза больше, чем во втором. Известно, что число символов в каждом алфавите не превышает 10 и на каждый символ приходится целое число бит. Определите мощность второго алфавита.
30. Требуется закодировать информацию объемом 1 000 бит с помощью алфавита, содержащего 16 знаков. Определить минимальную длину закодированного сообщения.
Количество информации и вероятность
Измерение информации в теории информации определяется как снятая неопределенность.
Получение информации (ее увеличение) одновременно означает увеличение знания, что, в свою очередь, означает уменьшение незнания или информационной неопределенности. Говорят, что сообщение, которое уменьшает неопределенность, существовавшую до его получения, в 2 раза, несет 1 бит информации. По сути, 1 бит информации соответствует выбору одного из двух равновероятных сообщений.
Книга лежит на одной из двух полок – верхней или нижней. Сообщение о том, что книга лежит на верхней полке, уменьшает неопределенность ровно вдвое и несет 1 бит информации. Сообщение о том, как упала монета после броска – «орлом» или «решкой», несет один бит информации.
Приближенно можно считать, что количество информации в сообщении о каком-либо событии совпадает с количеством вопросов, которые необходимо задать, ответ на которые может быть лишь «Да» или «Нет», чтобы получить ту же информацию.
Вероятностный подход был разработан в 1948 году основоположником теории информации Клодом Шенноном. Как было отмечено выше, информация – это снятая неопределенность. Степень неопределенности принято характеризовать с помощью понятия «вероятность».
Вероятность – величина, которая может принимать значения в диапазоне от 0 до 1. Она есть мера возможности наступления какого-либо события, которое может иметь место в одних случаях и не иметь места в других. Если событие никогда не может произойти, его вероятность считается равной 0. Если событие происходит всегда, его вероятность равна 1.
Чем больше вероятность события, тем больше уверенность в том, что оно произойдет, и тем меньше информации содержит сообщение об этом событии. Если вероятность события мала, то сообщение о том, что оно случилось, очень информативно.
| (1) |
| (1) |
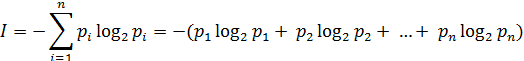
где n – число возможных состояний;
p1, ..., pn – вероятности отдельных состояний;
log2 – функция логарифма по основанию 2.
Знак минус перед суммой позволяет получить положительное значение для I, поскольку значение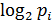 
всегда отрицательно.
1 бит – количество информации, посредством которого выделяется одно из двух равновероятных состояний объекта.
При оценке количества дискретной информации часто используется формула Хартли(2):
| (2) |
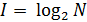
где N – число возможных равновероятных состояний;
log2 – функция логарифма по основанию 2.
Формула Хартли применяется в случае, когда вероятности состояний, в которых может находиться объект, одинаковые.
В качестве примера определим количество информации одного знака при двоичном кодировании (т.е. при использовании алфавита, состоящего из двух знаков 0 и 1). Если считать, что со знаками 0 и 1 в двоичном алфавите связаны одинаковые вероятности их появления, то
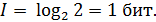
Таким образом, количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.
Рассмотрим несколько примеров.
Пример 1.3.1При бросании монеты сообщение о результате жребия (например, выпал «орел») несет 1 бит информации, поскольку количество возможных вариантов результата равно 2 («орел» или «решка»). Оба эти варианта равновероятны. Ответ может быть получен из решения уравнения:
2x = 2,
откуда следует:
х = 1 бит.
Вывод: сообщение об одном из двух равновероятных событий несет 1 бит информации.
Пример 1.3.2 В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)? Поскольку вынимание любого из 32 шаров равновероятно, то количество информации об одном выпавшем номере находится из уравнения:
2х = 32
32 = 25
Следовательно, х = 5 бит.
Ответ не зависит от того, шар с каким номером достали из барабана.
Пример 1.3.3 При игре в кости используется кубик с шестью гранями. Сколько бит информации получает игрок при каждом бросании кубика? Выпадение любой грани кубика равновероятно. Поэтому количество информации одного результата бросания находится из уравнения:
2х = 6
Решение этого уравнения:
х = 2,585 бит.
Пример 1.3.4 В коробке имеется 50 шаров. Из них 40 белых и 10 черных. Очевидно, вероятность того, что при вытаскивании «не глядя» попадется белый шар больше, чем вероятность попадания черного. Проверим это на практике.
Решение. Пусть рч – вероятность достать черный шар, рб – вероятность достать белый шар. Тогда:
рч = 10/50 = 0,2;
р6 = 40/50 = 0,8.
Отсюда видно, что вероятность достать белый шар в 4 раз больше, чем черный.
Определим количество информации в сообщениях о том, что достали белый шар или – черный шар:
iб = log 2 (l/0,8) = log 2 (l,25) = 0,321928;
iч = log 2 (l/0,2) = log 2 5 = 2,321928.
Пример 1.3.5 В пруду живут 8000 карасей, 2000 щук и 40 000 пескарей. Самая большая вероятность для рыбака – поймать в этом пруду пескаря, на втором месте – карася, на третьем – щуку. Проверим данные гипотезы с помощью вычислений.
Решение. Всего в пруду обитают 50000 рыб. Из предыдущих примеров можно догадаться, что вероятность попадания на удочку каждого из видов рыб равна его доле в общем количестве. Отсюда:
рк = 8000/50000 = 0,16;
рщ = 2000/50000 = 0,04;
рп = 40000/50000 = 0,8.
Из рассмотренных примеров можно сделать вывод: если N – это общее число возможных исходов какого-то процесса (доставание шара, получение оценки, ловля рыбы), и из них интересующее нас событие (вынимание белого шара, получение пятерки, попадание щуки) может произойти К раз, то вероятность этого события равна K/N.
Вероятностный метод применим и для алфавитного подхода к измерению информации, заключенной в тексте. Известно, что разные символы (буквы алфавита, знаки препинания и др.) встречаются в тексте с разной частотой и, следовательно, имеют разную вероятность. Значит, измерять информационный вес каждого символа в тексте так, как это делалось раньше (в предположении равновероятности), нельзя.
Пример 1.3.6 В алфавите племени МУМУ 4 буквы (А, У, М, К), один знак препинания (точка) и пробел, который служит для разделения слов. Подсчитали, что в популярном романе «Мумука» содержится всего 10000 знаков, из них: букв А – 4000, букв У – 1000, букв М – 2000, букв К – 1500, точек – 500, пробелов – 1000. Какой объем информации содержит книга?
Решение.Поскольку объем книги достаточно большой, то можно допустить, что вычисленная по ней частота встречаемости в тексте каждого из символов алфавита характерна для любого текста языке МУМУ. Подсчитаем частоту встречаемости каждого символа во всем тексте книги (т.е. вероятность) и информационные веса символов:
буква А: 4000/10000 = 0,4; iA=log 2 (1/0,4) = 1,321928;
буква У: 1000/10000 = 0,1; iУ=log 2 (1/0,1) = 3,1928;
буква М: 2000/10000 = 0,2; iМ=log 2 (1/0,2) = 2,321928;
буква К: 1500/10000 = 0,15; iК=log 2 (1/0,15) = 2,736966;
точка: 500/10000 = 0,05; iточка=log 2 (1/0,05) = 4,321928;
пробел: 1000/10000 = 0,1; iпробел=log 2 (1/0,1) = 3,321928.
Общий объем информации в книге вычислим как суму произведений информационного веса каждого символа на число повторений этого символа в книге:
I = iА х nА + iУ х nУ + iМ х nМ + iК х nК + iточка х nточка + iпробел х nпробел =
=1,321928 х 4000 + 3,1928 х 1000 + 2,321928 х 2000 + 2,736966 х 1500 + 4,321928 х 500 +
+ 3,321928 х 100 = 22841,84 бита.
Пример 1.3.7Определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака “пробел” для разделения слов.
По формуле Хартли (2): I = log234 ~ 5 бит
Однако, в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. В таблице 1.3.1 приведена вероятность частоты употребления различных знаков русского алфавита, полученная на основе анализа очень больших по объему текстов.
Воспользуемся для подсчета I формулой Шеннона (1): H ~ 4.72 бит. Полученное значение I, как и можно было предположить, меньше вычисленного ранее. Величина I, вычисляемая по этой формуле, является максимальным количеством информации, которое могло бы приходиться на один знак.
Таблица 1 – Частотность букв русского языка
| i | Символ | P(i) | i | Символ | P(i) | I | Символ | P(i) |
| 1 | _ | 0.175 | 12 | Л | 0.035 | 23 | Б | 0.014 |
| 2 | О | 0.090 | 13 | К | 0.028 | 24 | Г | 0.012 |
| 3 | Е | 0.072 | 14 | М | 0.026 | 25 | Ч | 0.012 |
| 4 | Ё | 0.072 | 15 | Д | 0.025 | 26 | Й | 0.010 |
| 5 | А | 0.062 | 16 | П | 0.023 | 27 | Х | 0.009 |
| 6 | И | 0.062 | 17 | У | 0.021 | 28 | Ж | 0.007 |
| 7 | T | 0.053 | 18 | Я | 0.018 | 29 | Ю | 0.006 |
| 8 | H | 0.053 | 19 | Ы | 0.016 | 30 | Ш | 0.006 |
| 9 | C | 0.045 | 20 | З | 0.016 | 31 | Ц | 0.004 |
| 10 | P | 0.040 | 21 | Ь | 0.014 | 32 | Щ | 0.003 |
| 11 | B | 0.038 | 22 | Ъ | 0.014 | 33 | Э | 0.003 |
| 34 | Ф | 0.002 |
ЗАДАЧИ
1. «Вы выходите на следующей остановке?» – спросили пассажира автобуса. «Нет», – ответил он. Сколько информации содержит ответ?
2. Какой объем информации содержит сообщение, уменьшающее неопределенность знаний в 4 раза?
3. Шар находится в одном из 64 ящичков. Сколько единиц информации будет содержать сообщение о том, где находится шар?
4. Вы подошли к светофору, когда горел красный свет. После этого загорелся желтый свет. Сколько информации вы при этом получили?
5. Группа студентов пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер 3. Сколько информации получили студенты из этого сообщения?
6. В корзине лежат 8 шаров. Все шары разного цвета. Сколько информации несет сообщение о том, что из корзины достали красный шар?
7. Была получена телеграмма: «Встречайте, вагон 7». Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?
8. В библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил студенту, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал студенту?
9. При угадывании целого числа в диапазоне от 1 до N было получено 7 бит информации. Чему равно N?
10. При угадывании целого числа в некотором диапазоне было получено 6 бит информации. Сколько чисел содержит этот диапазон?
11. Сообщение о том, что ваш друг живет на 10 этаже, несет 4 бита информации. Сколько этажей в доме?
12. Какое количество информации несет сообщение: «Встреча назначена на сентябрь».
13. В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?
14. В корзине лежат 32 клубка шерсти. Среди них 4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти?
15. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в корзине?
16. В ящике лежат перчатки (белые и черные). Среди них – 2 пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет 4 бита информации. Сколько всего пар перчаток было в ящике?
17. В группе 30 студентов. За контрольную работу по математике получено 6 пятерок, 15 четверок, 8 троек и 1 двойка. Какое количество информации в сообщении о том, что Иванов получил четверку?
18. Известно, что в ящике лежат 20 шаров. Из них 10 – черных, 5 – белых, 4 – желтых и 1 – красный. Какое количество информации несут сообщения о том, что из ящика случайным образом достали черный шар, белый шар, желтый шар, красный шар?
19. За семестр студент получил 100 оценок. Сообщение о том, что он получил четверку, несет 2 бита информации. Сколько четверок студент получил за четверть?
20. В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?
21. Сколько следует задать вопросов и как их следует формулировать, чтобы оценить сообщение о том, что вагон стоит на одном из 16 путей?
22. Шар находится в одной из 32 урн. Сколько единиц информации будет содержать сообщение о том, где он находится?
23. Система может принимать 128 различных равновероятных состояний. Каково количество информации в системе?
24. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)?
25. При игре в кости используется кубик с шестью гранями. Сколько бит информации получает игрок при каждом бросании кубика?
26. Частотный словарь русского языка – словарь вероятностей (частот) появления букв в произвольном тексте – приведен в таблице 1.3.1. Подсчитать количество информации, приходящейся на один символ, в следующем тексте:
Организационно-правовые формы предприятий в своей основе определяют форму их собственности, то есть, кому принадлежит предприятие, его основные фонды, оборотные средства, материальные и денежные ресурсы. В зависимости от формы собственности, в России в настоящее время различают три основные формы предпринимательской деятельности: частную, коллективную и контрактную.
Указание: составьте таблицу, аналогичную таблице 3.1.1, определив вероятность каждого символа в тексте как отношение количества одинаковых символов каждого значения ко всему числу символов в тексте. Затем по формуле Шеннона подсчитайте количество информации, приходящейся на один символ.
27. Подсчитать количество информации, приходящейся на один символ, в следующем тексте:
Общая технологическая схема изготовления сплавного транзистора напоминает схему изготовления диода, за исключением того, что в полупроводниковую пластинку производят вплавление двух навесок примесей с двух сторон. Вырезанные из монокристалла германия или кремния пластинки шлифуют и травят до необходимой толщины.
28. Подсчитать количество информации, приходящейся на один символ, в следующем тексте:
С конца пятнадцатого столетия в судьбах Восточной Европы совершается переворот глубокого исторического значения. На сцену истории Европы выступает новая крупная политическая сила – Московское государство. Объединив под своей властью всю северо-восточную Русь, Москва напряженно работает над закреплением добытых политических результатов и во внутренних, и во внешних отношениях.
29. Подсчитать количество информации, приходящейся на один символ, в следующем тексте:
Новые данные о физиологической потребности организма человека в пищевых веществах и энергии, а также выяснение закономерностей ассимиляции пищи в условиях нарушенного болезнью обмена веществ на всех этапах метаболического конвейера позволили максимально сбалансировать химический состав диет и их энергетическую ценность.
30. Подсчитать количество информации, приходящейся на один символ, в следующем тексте:
С любопытством стал я рассматривать сборище. Пугачев на первом месте сидел, облокотясь на стол и подпирая черную бороду своим широким кулаком. Черты лица его, правильные и довольно приятные, не изъявляли ничего свирепого. Все обходились между собою как товарищи и не оказывали никакого особенного предпочтения своему предводителю.
Системы счисления
Система счисления (с.с.) – способ представления чисел посредством цифровых знаков. Существуют два типа систем счисления: позиционные (например, десятичная) и непозиционные (например, римская). В современной практике используются только позиционные системы счисления, поэтому далее рассматриваем только их.
Всякая позиционная система счисления характеризуется основанием – количеством различных цифр, используемых для записи чисел. Значение каждой цифры, входящей в состав числа, зависит от её места (позиции) в ряду цифр, изображающих это число.
Десятичная система счисления, которая используется в повседневной практике, использует для записи чисел десять цифр (от 0 до 9).
Для составляющих ЭВМ элементов характерно два устойчивых состояния, поэтому в двоичной системе счисления используются только две цифры (0 и 1).
Восьмеричная и шестнадцатеричная системы счисления – вспомогательные. Применяются для записи машинных команд, некоторых констант и удобства программирования. Они удобны тем, что требуют для записи чисел соответственно в три и четыре раза меньше цифр, а перевод таких чисел в двоичную систему очень прост.
В восьмеричной системе счисления используется восемь цифр: 0, 1, 2, …, 7.
В шестнадцатеричной системе счисления для обозначения используется 16 различных цифр (0 – 15). А так как в десятичной системе имеется лишь 10 базовых цифр (0 – 9), то для обозначения остальных цифр берутся прописные латинские буквы: А=10, В=11, С=12, D=13, E=14, F=15.
В общем виде число А = anan-1…a0a-1a-2…a-m представляет сумму произведений степеней основания системы на коэффициенты, указанные в цифровых разрядах (3):
| (3) |
Вычисления в десятичной системе счисления являются наиболее удобными (для людей, но не для компьютеров). Поэтому для перевода числа из какой-либо позиционной системы в десятичную систему его представляют, используя приведённую выше позиционную запись числа (3), как сумму степеней основания q, которую затем подсчитывают.
ЗАДАЧИ
Целью решения задач является получение практических навыков работы с числами в позиционных системах счисления. Для выполнения заданий необходимо сначала получить исходные числа по следующим правилам:
1) первое число – ваш вариант задания (13) – порядковый номер в списке группы, увеличенный на любое число из диапазона от 33 до 99 (33). Получим формулу (4):
| (5) |
| (4) |
2) второе число – две последние цифры номера зачетной книжки (47), увеличенные на число в диапазоне от 33 до 99 (44). Получим формулу (5):
47 + 44 = 91.
3)третье число – сумма текущего календарного года и вашего варианта задания. Формула (6):
| (6) |
4) четвертое число – разница текущего календарного года и первого числа. Формула (7):
| (7) |
5) пятое число – частное от деления варианта задания на первое число. Формула (8):
| (8) |
6) шестое число – частное от деления третьего числа задания на первое число. Формула (9):
| (9) |
Дата добавления: 2018-05-12; просмотров: 2803; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!