Окремі випадки відносного руху
1 Відносний рух за інерцією
Якщо матеріальна точка|точка| рухається|суне| відносно|відносно| рухомої|жвавої,рухливої| системи відліку прямолінійно і рівномірно, то такий рух називається відносним рухом за інерцією.
отже 
2 Відносна рівновага
При спокої матеріальної точки|точки| відносно|відносно| рухомої|жвавої,рухливої| системи відліку її відносна швидкість і прискорення дорівнюють нулю, тобто
і 
, отже прискорення Коріоліса також|також| дорівнює нулю 
Умова відносної рівноваги має вигляд|вид|: 
3 Інерціальні системи відліку
Переносне прискорення в загальному|спільному| випадку обчислюється за формулою
,
де 
- прискорення точки|точки|, прийнятої за полюс (початок координат);
- кутова швидкість обертання рухомої|жвавої,рухливої| системи координат навколо|навкруг,довкола| вибраного полюса;
- кутове прискорення цього обертання (
);
- радіус-вектор руху точки|точки| відносно|відносно| полюса.
Якщо рухома|жвава,рухлива| система відліку рухається|суне| поступально, прямолінійно і рівномірно, то
, 
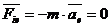і рівняння відносного руху мають вигляд|вид|: 
.
Рухома|жвава,рухлива| система відліку також|також| інерціальна|.
Лекція 5
Короткий зміст|вміст,утримання|: Внутрішні і зовнішні сили. Центр мас. Моменти інерції відносно|відносно| точки|точки| і осей. Теорема Штейнера.
Вступ|вступ| в динаміку системи
Механічною системою називається будь-яка система матеріальних точок|точок| і тіл.
|
|
|
Зовнішніми силами механічної системи називаються сили, з|із| якими на точки|точки| і тіла механічної системи діють точки|точки| і тіла, що не входять в дану систему.
Рівнодіюча|рівнодійна| всіх зовнішніх сил, прикладених до точки,|точки| позначається|значить| 
(від латинського exterior| - зовнішній).
Внутрішніми силами механічної системи називаються сили взаємодії між точками|точками| і тілами даної системи.
Рівнодіюча|рівнодійна| всіх внутрішніх сил, прикладених до точки,|точки| позначається|значить| 
(від латинського interior| - внутрішній).
Це розділення|поділ| є|з'являється,являється| умовним і залежить від того, яка механічна система розглядається|розглядує|.
Внутрішні сили системи володіють |слідуючими| властивостями:
Теорема. Головний вектор всіх внутрішніх сил системи (векторна сума) дорівнює нулю при будь-якому стані|достатку| системи. 
.
Доказ: Згідно однієї з аксіом динаміки, будь-які дві точки системи діють один на одного з|із| рівними по величині, але|та| протилежно направленими|спрямованими| силами. Векторна сума цих сил дорівнює нулю. Всі внутрішні сили є|з'являються,являються| великою кількістю таких парних сил. Тому сума всіх внутрішніх сил дорівнює нулю.
|
|
|
Теорема. Головний момент всіх внутрішніх сил системи (векторна сума) відносно|відносно| будь-якої точки|точки| або осі дорівнює нулю при будь-якому стані|достатку| системи. 
або 
.
Доказ: Будь-які дві точки системи діють один на одного з|із| рівними по величині, але|та| протилежно направленими|спрямованими| силами. Сума моментів цих сил відносно|відносно| будь-якої точки|точки| або осі дорівнює нулю. Всі внутрішні сили є|з'являються,являються| великою кількістю таких парних сил. Тому сума моментів всіх внутрішніх сил відносно|відносно| будь-якої точки|точки| або осі дорівнює нулю.
Диференціальні рівняння системи у векторній формі:
, 
Геометрія мас
Розглянемо|розглядуватимемо| механічну систему, яка складається з кінцевого|скінченного| числа 
матеріальних точок|точок| з|із| масами 
, а положення|становище| точок|точок| в просторі задається радіус-векторами 
.
Центром мас механічної системи називається геометрична точка|точка| С|із|, радіус-вектор якої 
визначається виразом|вираженням|
де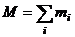 
- маса системи.
Якщо механічна система є суцільним тілом, то його розбивають на елементарні частинки|частки,часточки| з|із| нескінченно малими масами 
. Рисунок 5-1
|
|
|
Суми в межі переходять в інтеграли і центр мас визначається виразом:|вираженням|
Центр мас є|з'являється,являється| не матеріальною точкою|точкою|, а геометричною. Центр мас характеризує розподіл мас в системі.
Координати центру мас мають вигляд|вид|:
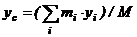
Для тіл типу|типа| тонкого листа|аркуша| (поверхня) і тонкого дроту (лінія) 
і 
, де 
- поверхнева|поверхова,зверхня| і лінійна щільність відповідно. Інтеграли обчислюються|обчисляють,вичисляють| по поверхні і лінії.
Моменти інерції
Для характеристики розподілу мас в тілах при розгляді обертальних рухів потрібно ввести|запроваджувати| поняття моментів інерції.
Момент інерції відносно|відносно| точки|точки|
Скалярна величина
або 
називається полярним моментом інерції відносно|відносно| точки О,
d – відстань від поточної точки|точки| до точки О.
Момент інерції відносно|відносно| осі
Скалярна величина 
або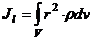 
називається моментом інерції відносно|відносно| осі l, r – відстань від точки|точки| до осі.
Моменти інерції однакових за формою однорідних тіл, виготовлених з|із| різних матеріалів, відрізняються один від одного. Характеристикою, не залежною від маси матеріалу, є|з'являється,являється| радіус інерції.
|
|
|
Величина 
називається радіусом інерції.
Момент інерції відносно|відносно| осі через радіус інерції відносно|відносно| цієї ж осі визначається виразом|вираженням| 
.
Моменти інерції відносно|відносно| осей координат
Відцентрові моменти інерції
Встановимо залежність між моментами інерції відносно|відносно| паралельних осей, одна з яких проходить через центр мас.
Теорема про моменти інерції відносно|відносно| паралельних осей (Теорема Штейнера)
Момент інерції системи відносно|відносно| будь-якої осі дорівнює моменту інерції відносно|відносно| паралельної осі, що проходить через центр мас, плюс добуток|добуток| маси системи на квадрат відстані між цими осями 
Доказ: Хай|нехай| є|наявний| дві декартові системи координат 
і 
, осі яких паралельні. Початок системи знаходиться|перебуває| в центрі мас системи. Доведемо теорему для осей 
і 
.
Рисунок 5-2
; 
Координати зв'язані між собою співвідношеннями:
, 
, 
, 
, 
.
Отже 
, що і потрібно було довести.
Головними осями інерції називаються осі, в яких відцентрові моменти інерції дорівнюють нулю.
Моменти інерції тіла відносно|відносно| головних осей інерції називаються головними моментами інерції тіла.
Тензор інерції і тензор інерції для головних осей:
Лекція 6
Короткий зміст|вміст,утримання|: Загальні|спільні| теореми динаміки системи і твердого тіла: Кількість руху системи. Теорема про зміну кількості руху системи. Закони збереження|зберігання| кількості руху. Теорема про рух центру мас. Момент кількості руху твердого тіла відносно|відносно| осі обертання при обертальному русі твердого тіла. Момент кількості руху системи. Теорема про зміну моменту кількості руху системи. Закони збереження|зберігання| моменту кількості руху. Кінетична енергія системи. Кінетична енергія твердого тіла. Теорема про зміну кінетичної енергії системи.
Загальні|спільні| теореми динаміки системи і твердого тіла
Кількість руху системи
Кількістю руху системи матеріальних точок|точок| 
називається векторна сума кількостей рухів окремих точок системи.
Одиницею вимірювання|виміру| кількості руху в СІ є|з'являється,являється| – 
Кількість руху системи можна виразити|виказувати,висловлювати| через масу системи і швидкість центру мас 
Дата добавления: 2018-05-12; просмотров: 377; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!