Теорема про прискорення точок плоскої фігури
Прискорення довільної точки твердого тіла, що бере участь в плоскому русі, можна знайти як геометричну суму прискорення полюса і прискорення даної крапки в обертальному русі навколо полюса.
Для доказу цього положення використовуємо теорему складання прискорень тічки в складеному русі. Приймемо за полюс точку 
. Рухому систему координат переміщатимемо поступально разом з полюсом (рисунок 6-7 а). Тоді відносним рухом буде обертання навколо полюса. Відомо, що кориолисово прискорення у разі переносної поступальної ходи рівне нулю, тому
.
Оскільки в поступальній ході прискорення всіх крапок однакові і рівні прискоренню полюса, маємо 
.
Прискорення крапки при русі по колу зручно представити у вигляді суми доцентровою і обертальною складових:
.
Отже
.
Напрями складових прискорення 
показані на рисунок 6-7а.
Нормальна (доцентрова) складова відносного прискорення визначається формулою
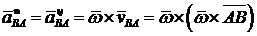
Величина його рівна 
Вектор 
направлений уздовж відрізання АВ до полюса А (центром обертання навколо 
є ).
Рисунок 6-7
Дотична (обертальна) складова відносного прискорення визначається формулою
.
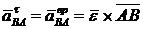Модуль цього прискорення знаходиться через кутове прискорення 
. Вектор 
направлений перпендикулярно до АВ у бік кутового прискорення (у бік кутової швидкості, якщо рух прискорений і в протилежну сторону обертання, якщо рух сповільнений).
Величина повного відносного прискорення визначається по теоремі Піфагора:
|
|
|
.
Вектор відносного прискорення будь-якої точки плоскої фігури відхилений від прямою, що сполучає дану крапку з полюсом на кут 
, визначуваний формулою
.
На рисунку 6-7б показано, що цей кут однаковий для всіх точок тіла.
Слідство з теореми про прискорення
Кінці векторів прискорень точок прямолінійного відрізку на плоскій фігурі лежать на одній прямій і ділять її на частини, пропорційні відстаням між точками.
Доказ цього затвердження слідує з рисунка:
.
Рисунок 6-8
Методи визначення прискорень точок тіла при плоскому його русі ідентичні відповідним методам визначення швидкостей.
Миттєвий центр прискорень
У будь-який момент часу в площині рухомої фігури існує одна єдина точка, прискорення якої рівне нулю. Ця точка називається миттєвим центром прискорень (МЦП).
Доказ виходить із способу визначення положення цієї точки. Приймемо за полюс точку А, припускаючи, що відоме її прискорення. Розкладаємо рух плоскої фігури на поступальне і обертальне. Користуючись теоремою складання прискорень, записуємо прискорення шуканої
Рисунок 6-9 точки і прирівнюємо його нулю.
Звідси слідує, що 
, т. є. відносне прискорення точки Q рівне прискоренню полюса А по величині і направлено в протилежну сторону.
|
|
|
Це можливо тільки в тому випадку, якщо кути нахилу відносного прискорення і прискорення полюса А до прямою, що сполучає точку Q, з полюсом А однакові.
, 
, 
.
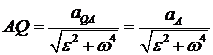Приклади знаходження МЦП.
Розглянемо способи знаходження положення МЦП.
Приклад
Відомі 
(рисунок 6-10 а).
Визначаємо кут 
. Відкладаємо кут у напрямі кутового прискорення (у бік обертання при прискореному обертанні і проти — при сповільненому), від напряму відомого прискорення точки і будуємо промінь. На побудованому промені відкладаємо відрізок довжиною AQ.
Рисунок 6-10
Короткий зміст|вміст,утримання|: Складний рух точки|точки| в загальному|спільному| випадку: абсолютна і відносна похідні, складання швидкостей, складання прискорень. Прискорення Коріоліса. Правило Жуковського.
Складний рух точки|точки| в загальному|спільному| випадку
Абсолютна і відносна похідні
При розгляді складного руху точки|точки| необхідно розглядати|розглядувати| зміну векторних величин з часом по відношенню до систем відліку, рухомих один відносно|відносно| одного.
Розглянемо|розглядуватимемо| довільний вектор 
в двох системах відліку: рухомою|жвавою,рухливою| і нерухомою. У рухомій|жвавій,рухливій| системі відліку тільки|лише| проекції вектора 
є|з'являються,являються| функціями часу, в нерухомій системі відліку окрім|крім| проекцій, функціями часу є|з'являються,являються| і одиничні|поодинокі| вектора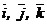 
(вони змінюють|зраджують| свій напрям|направлення| в просторі).
|
|
|
(9-1)
Рисунок 9-1
Введемо|запроваджуватимемо| позначення 
- абсолютна похідна – похідна в нерухомій системі відліку; 
- відносна похідна – похідна в рухомій|жвавій,рухливій| системі відліку.
Встановимо залежність між абсолютною і відносною похідними. Обчислимо|обчислятимемо,вичислятимемо| абсолютну похідну за часом від вектора використовуючи формулу (9-1). Отримаємо|одержуватимемо|
(9-2)
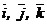Перші три доданки враховують зміну вектора при незмінних і тому складають відносну похідну, тобто
. (9-3)
Похідні за часом від одиничних|поодиноких| векторів визначимо за формулами Пуассона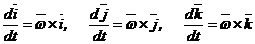 
де 
- кутова швидкість обертальної частини|частки| руху навколо|навкруг,довкола| точки|точки| О рухомої|жвавої,рухливої| системи відліку відносно|відносно| нерухомої.
|
|
|
Після|потім| підстановки отримуємо |одержуємо|
. (9-4)
Отримана|одержувати| формула залежності похідних вектора в двох системах відліку рухомих один відносно|відносно| другого (формула Бура).
Складання швидкостей
Хай|нехай| система відліку O1x1y1z1| - нерухома, а система відліку Oxyz| -рухома|жвава,рухлива|. Рух точки|точки| відносно|відносно| основної нерухомої системи відліку O1x1y1z1|називається абсолютним. Рух точки|точки| відносно|відносно| рухомої|жвавої,рухливої| системи відліку Oxyz|називається відносним. Переносним рухом точки|точки| називається рух, який вона здійснює|скоює,чинить| разом з рухомою|жвавою,рухливою| системою відліку, як точка|точка|, що жорстко скріпляється з|із| цією системою в даний момент часу. Відносні швидкість і прискорення позначають|значать| 
і 
, переносні - 
і 
, а абсолютні - 
і 
.
Рисунок 9-2
Рух рухомої|жвавої,рухливої| системи відліку відносно|відносно| нерухомої можна охарактеризувати швидкістю її поступальної ходи 
, наприклад, разом з точкою|точкою| О і вектором кутової швидкості її обертання навколо|навкруг,довкола| О.
Теорема. Швидкість абсолютного руху точки|точки| дорівнює векторній сумі переносної і відносної швидкостей: 
Доказ. Розглянемо|розглядуватимемо| рух точки|точки| 
. Положення|становище| точки|точки| відносно|відносно| нерухомої системи відліку визначається вектором 
, а відносно|відносно| рухомої|жвавої,рухливої| вектором 
. Положення|становище| точки|точки| 
відносно|відносно| нерухомої системи відліку визначається вектором 
. Для будь-якого моменту часу виконується тотожність 
.
Продиференціюємо його за часом (обчислимо|обчислятимемо,вичислятимемо| похідні в нерухомій системі відліку) і отримаємо|одержуватимемо|
(9-5)
За визначенням 
- абсолютна швидкість точки |точки| ,
- абсолютна швидкість точки|точки| . Для обчислення|підрахунку| 
застосуємо формулу Бура. Маємо 
. Відносна похідна 
- є|з'являється,являється| відносною швидкістю точки|точки| по відношенню до нерухомої системи відліку, а - кутова швидкість обертання рухомої|жвавої,рухливої| системи відліку.
Таким чином з|із| (9-5) отримуємо|одержуємо|
(9-6)
Швидкість 
є|з'являється,являється| швидкістю точки вільного твердого тіла, що скріпляється з|із| рухомою|жвавою,рухливою| системою координат, з|із| якою в даний момент співпадає|збігається| точка|точка| в русі тіла відносно|відносно| нерухомої системи відліку. Це є переносна швидкість точки|точки| .
Остаточно отримуємо|одержуємо|
, (9-7)
що і потрібно було довести.
Складання прискорень в загальному|спільному| випадку переносного руху
Теорема (кінематична теорема Коліоліса). Абсолютне прискорення точки|точки| є|з'являється,являється| векторною сумою трьох прискорень - переносного, відносного і Коріоліса. 
Доказ. Абсолютне прискорення точки|точки| визначимо обчисленням|підрахунком| повної|цілковитої| похідної за часом від абсолютної швидкості.
Для похідних від векторів 
і 
застосуємо формулу Бура. Отримаємо|одержуватимемо|
Враховуючи, що 
,
,,
,
отримаємо|одержуватимемо| для абсолютного прискорення
(9-8)
У цій формулі перші три доданки є|з'являються,являються| переносним прискоренням для точки|точки| 
.
Останній доданок називається прискоренням Коріоліса (іноді|інколи| його називають додатковим або поворотним прискоренням) і позначається|значить|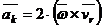 
.
У результаті формула (9-8) приймає вигляд|вид|
(9-9)
що і потрібно було довести.
Прискорення Коріоліса
Теорема (Правило Жуковського). Модуль прискорення Коріоліса дорівнює подвоєному добутку|добутку| кутової швидкості переносного обертання на модуль проекції відносної швидкості на площину|плоскість|, перпендикулярну осі переносного обертання; щоб|аби| отримати|одержувати| напрям|направлення| прискорення Коріоліса, необхідно вектор проекції відносної швидкості повернути|обернути| на 
навколо|навкруг,довкола| осі, паралельної осі переносного обертання у напрямі цього обертання.
ДИНАМІКА
Лекція 1
Короткий зміст|вміст,утримання|: Вступ|вступ| в динаміку. Аксіоми класичної механіки. Системи одиниць. Диференціальні рівняння руху точки|точки|. Основні завдання|задачі| динаміки. Основні види прямолінійного руху точки|точки|.
Вступ|вступ|
У динаміці вивчаються механічні рухи матеріальних об'єктів під дією сил. Простим матеріальним об'єктом є|з'являється,являється| матеріальна точка|точка|.
Матеріальна точка|точка| - це модель матеріального тіла будь-якої форми, розмірами якого можна нехтувати і прийняти за геометричну точку|точку|, що має певну масу.
Складніші матеріальні об'єкти – механічні системи і тверді тіла складаються з набору матеріальних точок|точок|.
Рух матеріальних об'єктів завжди відбувається|походить| в просторі відносно|відносно| певної системи відліку і в часі. Простір вважається|лічить| тривимірним|трьохмірним| евклідовим| простором, властивості якого не залежать від рухомих в ньому матеріальних об'єктів.
Час в класичній механіці не пов'язаний з простором і рухом матеріальних об'єктів. У всіх системах відліку рухомих один відносно|відносно| другого воно протікає однаково.
Аксіоми класичної механіки
Перша аксіома або закон інерції.
Матеріальна точка|точка|, на яку не діють сили або діє рівноважна система сил володіє здатністю|здібністю| зберігати свій стан|достаток| спокою або рівномірного і прямолінійного руху відносно інерційної| системи відліку.
Матеріальна точка|точка|, на яку діє рівноважна система сил називається ізольованою матеріальною точкою|точкою|.
Рівномірний і прямолінійний рух точки|точки| називається рухом за інерцією.
Дата добавления: 2018-05-12; просмотров: 926; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!