Друга аксіома або основний закон динаміки.
Прискорення матеріальної точки|точки| відносно|відносно| інерційної системи відліку пропорційно прикладеній до точки|точки| сили і направлено|спрямований| по цій силі.


Позитивний коефіцієнт пропорційності m, характеризує інертні властивості матеріальної точки|точки| і називається масою точки|точки|.
Рисунок 1-1
Маса не залежить від характеристик руху точки|точки| і від природи сил. Маса вважається|лічить| постійною величиною і залежить тільки|лише| від самої матеріальної точки|точки|.
Сила, прикладена до матеріальної точки|точки|, завжди має матеріальне джерело у вигляді інших матеріальних тіл, які діють на точку|точку| шляхом контакту при безпосередньому зіткненні з|із| нею або на відстані.|
 Третя аксіома або закон про рівність сил дії і протидії.
Третя аксіома або закон про рівність сил дії і протидії.
Сили взаємодії двох матеріальних точок|точок| рівні по величині і протилежні за напрямом|направленню|. 
Рисунок 1-2
Четверта аксіома або закон незалежної дії сил.
При одночасній дії на матеріальну точку декількох сил прискорення точки|точки| відносно|відносно| інерційної системи відліку від дії кожної окремої сили не залежить від наявності інших, прикладених до точки|точки|, сил і повне|цілковите| прискорення дорівнює векторній сумі прискорень від дії окремих сил.
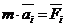

Аксіоми класичної механіки добре узгоджуються з|із| результатами дослідів.
Системи одиниць
|
|
|
1 кГ| = 9,8 Н 36 км/год = 10 м/сек 1 Т.е.м. = 9,8 кг
Диференціальні рівняння руху точки|точки|
Основне рівняння динаміки 
можна записати так  або так
або так 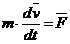
Проектуючи рівняння  на осі координат отримуємо|одержуємо|
на осі координат отримуємо|одержуємо|
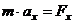


оскільки|тому що|  ,
,  ,
,  , то
, то



Окремі випадки:
а) Точка|точка| рухається|суне| в площині|плоскості|. Вибираємо в площині|плоскості| координати xOy|, отримуємо|одержуємо| 

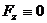
б) Точка|точка| рухається|суне| по прямій. Вибираємо на прямій координату Ox,| отримуємо|одержуємо| 

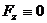
Основне рівняння динаміки  можна спроектувати на природні рухомі|жваві,рухливі| осі.
можна спроектувати на природні рухомі|жваві,рухливі| осі.






Ця форма рівнянь зручна для дослідження деяких випадків польоту снарядів і ракет.
Основні завдання|задачі| динаміки
Перше або пряме завдання|задача|:
Відома маса (m) точки|точки| і закон її руху, необхідно знайти силу, що діє на точку|точку|.



Обчислюємо|обчисляємо,вичисляємо| другі похідні за часом від координат точки, множимо|множимо| їх на масу і отримуємо|одержуємо| проекції сили на осі координат



Знаючи проекції сили на осі координат, визначуваний модуль сили і її направляючі|спрямовувати,скеровувати| косинуси:


Приклад|зразок|: Рух точки|точки| в площині|плоскості| xOy| визначається рівняннями:
|
|
|

 ;
;  ;
;  ;
;  час.
час.
Рішення|розв'язання,вирішення,розв'язування|:  ;
;
 ;
;
 ;
;  .
.
Рисунок 1-3
 - рівняння траєкторії в координатній формі (еліпс).
- рівняння траєкторії в координатній формі (еліпс).
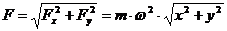
 ;
; 
Друге або зворотне завдання|задача|:
Відома маса точки|точки| і сила, що діє на точку|точку|, необхідно визначити закон руху цієї точки|точки|.
Розглянемо|розглядуватимемо| рішення цієї задачі в декартовій системі координат. Сила залежить від часу, координат точки, її швидкості та інших причин.
 ,
,  ,
,

З|із| теорії звичайних диференціальних рівнянь відомо, що вирішення одного диференціального рівняння другого порядку|ладу| містить|утримує| дві довільні постійні. Для випадку системи трьох звичайних диференціальних рівнянь другого порядку|ладу| є|наявний| шість довільних постійних: 
Кожна з координат  рухомої точки після|потім| інтеграції системи рівнянь залежить від часу і всіх шести довільних постійних, тобто
рухомої точки після|потім| інтеграції системи рівнянь залежить від часу і всіх шести довільних постійних, тобто



До цих рівнянь необхідно додати|добавляти| початкові умови:
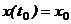 ,
, 

 ,
, 

Використовуючи ці початкові умови можна отримати|одержувати| шість алгебраїчних рівнянь для визначення шести довільних постійних  .
.
Основні види прямолінійного руху точки|точки|
|
|
|
Диференціальне рівняння прямолінійного руху точки|точки| уздовж|вздовж,уподовж| осі Ох має вигляд|вид|:
 . Початкові умови
. Початкові умови 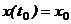
 .
.
Найбільш важливі|поважні| випадки
1 Сила постійна 


Маємо рух який рівномірно змінюється (рух з|із| постійним прискоренням)
2 Сила залежить від часу 



3 Сила залежить від координати або швидкості
Сила, залежна від координати -  , створює пружні тіла при їх деформації (наприклад, стисла або розтягнута пружина) -
, створює пружні тіла при їх деформації (наприклад, стисла або розтягнута пружина) - 
Сила, залежна від швидкості руху -  це сила опору (повітря, води і так далі).
це сила опору (повітря, води і так далі).
У цих випадках рішення задачі спрощується.
Лекція 2
Короткий зміст|вміст,утримання|: Вільні коливання без опору. Поняття про фазову площину|плоскість|. Вільні коливання в полі постійної сили. Паралельне включення|приєднання| пружних елементів. Послідовне включення|приєднання| пружних елементів. Вимушені|змушені| коливання без опору. Резонанс. Вільні коливання з|із| в'язким опором. Вимушені|змушені| коливання з|із| в'язким опором.
Вільні коливання без опору
Існують пристрої|устрої| (пружні елементи), які створюють силу, пропорційну|пропорціональну| їх подовженню|видовженню|.  . Цю силу називають оновлюючою або центральною силою. Коефіцієнт пропорційності називається жорсткістю пружного елементу.
. Цю силу називають оновлюючою або центральною силою. Коефіцієнт пропорційності називається жорсткістю пружного елементу.
|
|
|
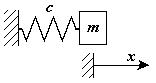
Диференціальне рівняння руху точки|точки| з|із| масою  , закріпленою на пружному елементі, має вигляд|вид|:
, закріпленою на пружному елементі, має вигляд|вид|:
 або
або  , де
, де 
Рисунок 2-1
Початкові умови мають вигляд|вид|: при 
 ,
,  .
.
Це диференціальне рівняння вільних коливань матеріальної точки|точки| без опору.
Характеристичне рівняння має вигляд|вид|: 
Коріння характеристичного рівняння дорівнює: 
Рішення|розв'язання,вирішення,розв'язування| має вигляд|вид|:


 ,
, 


 - амплітуда коливань;
- амплітуда коливань; 
де  - кругова або циклічна частота коливань (власна частота). Вимірюється в
- кругова або циклічна частота коливань (власна частота). Вимірюється в  .
.
 - фазовий кут|ріг,куток| (або просто фаза);
- фазовий кут|ріг,куток| (або просто фаза);
 - період коливань;
- період коливань;
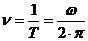 - частота коливань (1 кол|кілок|./cек=1 Гц)
- частота коливань (1 кол|кілок|./cек=1 Гц)
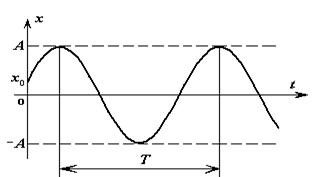
Рисунок 2-2
Рух матеріальної точки|точки| – це вільні гармонійні коливання з|із| постійною амплітудою. Амплітуда коливань залежить від початкових умов і кругової частоти.
Лекція 3
Короткий зміст|вміст,утримання|: Загальні|спільні| теореми динаміки точки|точки|. Кількість руху точки|точки|. Елементарний і повний|цілковитий| імпульс сили. Теорема про зміну кількості руху точки|точки|. Момент кількості руху точки|точки|. Робота сили. Потужність. Кінетична енергія точки|точки|. Теорема про зміну кінетичній енергії точки|точки|. Принцип Даламбера для матеріальної точки.|точки|
ЗАГАЛЬНІ|спільні| ТЕОРЕМИ ДИНАМІКИ ТОЧКИ|точки|
Для вирішення багатьох завдань|задач| динаміки замість безпосереднього інтегрування диференціальних рівнянь руху, виявляється|опиняється| ефективнішим користуватися так званими загальними|спільними| теоремами, які є|з'являються,являються| наслідком основного закону динаміки.
Кількість руху точки|точки|
Кількістю руху матеріальної точки|точки|  називається вектор, який дорівнює добутку|добутку| маси точки|точки|
називається вектор, який дорівнює добутку|добутку| маси точки|точки|  на її швидкість
на її швидкість  .
. 
Кількість руху точки|точки| у фізиці часто називають імпульсом матеріальної точки|точки|.
Проекції кількості руху точки|точки| на прямокутні декартові осі координат дорівнюють:
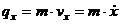 ,
,  ,
, 
Одиницею вимірювання|виміру| кількості руху в СІ є|з'являється,являється| – 
Елементарний і повний|цілковитий| імпульс сили
Дія сили 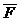 на матеріальну точку|точку| в перебігу часу
на матеріальну точку|точку| в перебігу часу  можна охарактеризувати елементарним імпульсом сили
можна охарактеризувати елементарним імпульсом сили  .
.
Повний|цілковитий| імпульс сили 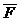 за час
за час  , або імпульс сили
, або імпульс сили  , визначається по формулі
, визначається по формулі  . (Повний|цілковитий| інтеграл за час
. (Повний|цілковитий| інтеграл за час  від елементарного імпульсу).
від елементарного імпульсу).
В окремому випадку, якщо сила 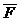 постійна і по величині і за напрямом|направленню| (
постійна і по величині і за напрямом|направленню| (  ),
),  .
.
Проекції імпульсу сили на прямокутні декартові осі координат дорівнюють:
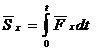


Одиницею вимірювання|виміру| імпульсу в СІ є|з'являється,являється| – 
Теорема про зміну кількості руху точки|точки|
Теорема. Похідна за часом від кількості руху точки|точки| дорівнює силі, що діє на точку|точку|.
Запишемо основний закон динаміки у вигляді|виді|  . Оскільки|тому що| маса постійна, то внесемо її під знак похідної.
. Оскільки|тому що| маса постійна, то внесемо її під знак похідної.
Тоді  , (*)
, (*)
що і потрібно було довести.
У проекціях на координатні осі рівняння (*) можна представити|уявляти| у вигляді|виді|:



Теорема імпульсів (у диференціальній формі). Диференціал від кількості руху точки|точки| дорівнює елементарному імпульсу сили, що діє на точку|точку|.
Помножимо ліву і праву частини|частки| рівняння (*) на  і отримаємо|одержуватимемо|
і отримаємо|одержуватимемо|
 (**)
(**)
У проекціях на координатні осі отримуємо|одержуємо|:
 ,
,
 ,
,
 .
.
Теорема імпульсів (в інтегральній формі). Зміна кількості руху точки|точки| за будь-який проміжок часу дорівнює імпульсу сили за цей же проміжок часу.
Інтегруючи обидві частини|частки| рівняння (**) за часом в межах від нуля до  отримуємо|одержуємо|:
отримуємо|одержуємо|:
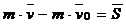
У проекціях на координатні осі отримуємо|одержуємо|:
 ,
,
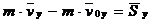 ,
,

Момент кількості руху точки|точки|
У деяких завданнях|задачах| в якості динамічної характеристики рухомої точки|точки| замість самої кількості руху розглядають|розглядують| його момент відносно|відносно| будь-якого центру або осі. Ці моменти визначаються також як і моменти сили.
Моментом кількості руху матеріальної точки|точки| відносно|відносно| деякого центру О називається вектор, який визначається рівністю 
Момент кількості руху точки|точки| називають також кінетичним моментом.
Момент кількості руху відносно|відносно| будь-якої осі  , що проходить через центр О, дорівнює проекції вектора кількості руху
, що проходить через центр О, дорівнює проекції вектора кількості руху  на цю вісь
на цю вісь  .
.
 Якщо кількість руху
Якщо кількість руху 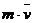 задана своїми проекціями
задана своїми проекціями  на осі координат і задані| координати
на осі координат і задані| координати  точки
точки  в просторі, то момент кількості руху
в просторі, то момент кількості руху  відносно початку координат обчислюється|обчисляє,вичисляє| таким чином:
відносно початку координат обчислюється|обчисляє,вичисляє| таким чином:
 Рисунок 3-1
Рисунок 3-1
Проекції моменту кількості руху на осі координат дорівнюють:
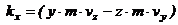


Одиницею вимірювання|виміру| кількості руху в СІ є|з'являється,являється| –  .
.
Теорема про зміну моменту кількості руху точки|точки|
Теорема. Похідна за часом від моменту кількості руху точки|точки|, взятої відносно|відносно| будь-якого|будь-якого| центру, дорівнює моменту сили, що діє на точку|точку| відносно|відносно| того ж центру.

Доказ: Візьмемо диференціал від рівняння моменту кількості руху за часом 

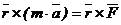 , отже
, отже  (*)
(*)
що і потрібно було довести.
Теорема. Похідна за часом від моменту кількості руху точки|точки|, узятої відносно|відносно| будь-якої осі, дорівнює моменту сили, що діє на точку|точку| відносно|відносно| тієї ж осі.
Для доказу досить спроектувати векторне рівняння (*) на цю вісь. Для осі  це виглядатиме так:
це виглядатиме так: 
Слідства з|із| теорем:
1. Якщо момент сили відносно|відносно| точки|точки| дорівнює нулю, то момент кількості руху відносно|відносно| цієї точки|точки| величина постійна.
 ,
, 

2. Якщо момент сили відносно|відносно| осі дорівнює нулю, то момент кількості руху відносно|відносно| цієї осі величина постійна.
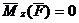 ,
, 
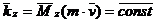
Робота сили. Потужність
Одна з основних характеристик сили, що оцінюють дію сили на тіло при деякому його переміщенні.
 Елементарна робота сили скалярна величина дорівнює добутку|добутку| елементарного переміщення на проекцію сили на це переміщення.
Елементарна робота сили скалярна величина дорівнює добутку|добутку| елементарного переміщення на проекцію сили на це переміщення.
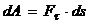 .
.  ,
,

Рисунок 3-1
Одиницею вимірювання|виміру| роботи в СІ є|з'являється,являється| – 
При  при
при 
Окремі випадки: 


Елементарне переміщення дорівнює диференціалу радіус-вектора точки додатку|застосування| сили.
Елементарна робота сили дорівнює скалярному добутку|добутку| сили на елементарне переміщення або на диференціал радіус-вектора точки додатку|застосування| сили.

Елементарна робота сили дорівнює скалярному добутку|добутку| елементарного імпульсу сили на швидкість точки|точки|.

Якщо сила  задана своїми проекціями (
задана своїми проекціями (  ) на осі координат і елементарне переміщення задано своїми проекціями (
) на осі координат і елементарне переміщення задано своїми проекціями ( 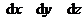 ) на осі координат, то елементарна робота сили дорівнює:
) на осі координат, то елементарна робота сили дорівнює:
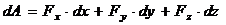 (аналітичний вираз|вираження| елементарної роботи).
(аналітичний вираз|вираження| елементарної роботи).
Робота сили на будь-якому кінцевому|скінченному| переміщенні 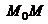 дорівнює узятому уздовж|вздовж,уподовж| цього переміщення інтегралу від елементарної роботи.
дорівнює узятому уздовж|вздовж,уподовж| цього переміщення інтегралу від елементарної роботи.

Потужністю сили називається величина, що визначає роботу, що здійснюється|скоює,чинить| силою|силоміць| в одиницю часу. У загальному|спільному| випадку потужність дорівнює першій похідній за часом від роботи.
 ,
, 
Потужність дорівнює скалярному добутку|добутку| сили на швидкість.
Одиницею вимірювання|виміру| потужності в СІ є|з'являється,являється| – 
У техніці за одиницю сили береться  .
.
Приклад|зразок|. Робота сили тяжіння
 Хай|нехай| точка М, на яку діє сила тяжіння Р, переміщається з|із| положення|становища|
Хай|нехай| точка М, на яку діє сила тяжіння Р, переміщається з|із| положення|становища|  в положення|становище|
в положення|становище|  . Виберемо осі координат так, щоб вісь
. Виберемо осі координат так, щоб вісь  була направлена|спрямована| вертикально вгору|угору|.
була направлена|спрямована| вертикально вгору|угору|.
Тоді,  ,
, 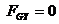 ,
,  і
і
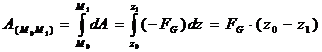
Робота сили тяжіння дорівнює взятому із|із| знаком плюс або мінус добутку|добутку| модуля сили на вертикальне переміщення точки її застосування.
Рисунок 3-2
Робота позитивна, якщо початкова точка вище кінцевої|скінченною|, і негативна|заперечна| - якщо початкова точка нижче кінцевої|скінченною|.
Кінетична енергія точки|точки|
Кінетичною енергією матеріальної точки|точки| (або її живою|жвавою| силою) називають половину добутку|добутку| маси точки|точки| на квадрат її швидкості.
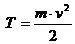
Теорема про зміну кінетичній енергії точки|точки|
Теорема. Диференціал кінетичної енергії точки|точки| дорівнює елементарній роботі сили, що діє на точку|точку|.

Доказ: Основний закон динаміки  .
.
Помножимо ліву і праву частини|частки| рівняння на  :
:  . Справа отримуємо|одержуємо|
. Справа отримуємо|одержуємо|  - елементарна робота.
- елементарна робота.
 - диференціал від кінетичної енергії.
- диференціал від кінетичної енергії.
 що і потрібно було довести.
що і потрібно було довести.
Теорема. Похідна за часом від кінетичної енергії точки|точки| дорівнює потужності, що підводиться до цієї точки|точки|.

Теорема. Зміна кінетичній енергії точки|точки| на будь-якому переміщенні дорівнює роботі сили, що діє на точку|точку| на цьому ж переміщенні.

Принцип Даламбера для матеріальної точки|точки|
Рівняння руху матеріальної точки|точки| відносно інерційної| системи відліку під дією прикладених активних сил і сил реакції зв'язків має вигляд|вид|:
 ,
,
 - рівнодіюча|рівнодійна| активних сил,
- рівнодіюча|рівнодійна| активних сил, 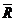 - рівнодіюча|рівнодійна| сил реакції зв'язків.
- рівнодіюча|рівнодійна| сил реакції зв'язків.
Силою|силоміць| інерції матеріальної точки|точки| називають добуток|добуток| маси точки|точки| на вектор прискорення, узяте із|із| зворотним знаком, тобто  .
.
Якщо використовувати поняття сили інерції, то основний закон динаміки приймає вигляд|вид|: 
Принцип Даламбера. При русі матеріальної точки|точки| активні сили і сили реакції зв'язків разом з силою інерції точки|точки| утворюють рівноважну систему сил.
Принцип Даламбера називають ще методом кінетостатики. Завдання|задачі| динаміки за допомогою цього методу зводяться до завдань|задач| статики.
Лекція 4
Короткий зміст|вміст,утримання|: Динаміка скованої матеріальної точки|точки|. Відносний рух матеріальної точки|точки|. Окремі випадки.
Динаміка скованої матеріальної точки|точки|
Скованою матеріальною точкою|точкою| називається точка|точка|, свобода руху якої обмежена.
Тіла, що обмежують свободу руху точки|точки| називаються зв'язками.
Хай|нехай| зв'язком є поверхня будь-якого тіла, по якій рухається|суне| точка|точка|. Тоді координати точки повинні задовольняти рівнянню цієї поверхні, яке називається рівнянням зв'язку.

Якщо точка|точка| вимушена|змушена| рухатися|сунути| по деякій лінії, то рівняннями зв'язку є|з'являються,являються| рівняння цієї лінії.
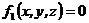 ,
, 
Таким чином, рух скованої матеріальної точки|точки| залежить не тільки|не лише,не те що| від прикладених до неї активних сил і початкових умов, але|та| так само від наявних зв'язків. При цьому значення початкових параметрів повинно задовольняти рівнянням зв'язків.
Зв'язки бувають двосторонні|двобічні| або такі, що утримують і односторонні|однобічні| або такі, що не утримують.
Зв'язок називається двостороннім,|двобічним| якщо обмеження, що накладаються на координати точки виражаються|виказують,висловлюють| у формі|у формі| рівності, що визначає криві або поверхні в просторі, на яких повинна знаходиться|перебуває| точка|точка|.

Приклад|зразок|
Матеріальна точка|точка| підвішена на стрижні|стержні| довжиною  .
.
Рівняння зв'язку має вигляд|вид|:

Рисунок 4-1
Зв'язок називається одностороннім,|однобічним| якщо обмеження, що накладаються на координати точки виражаються|виказують,висловлюють| у формі|у формі| нерівностей. Односторонній|однобічний| зв'язок перешкоджає переміщенню точки|точки| лише в одному напрямі|направленні| і допускає її переміщення в інших напрямах|направленнях|.
 Матеріальна точка|точка| підвішена на нитці довжиною
Матеріальна точка|точка| підвішена на нитці довжиною  .
.
Рівняння зв'язку має вигляд|вид|:

Рисунок 4-2
Принцип звільнення|визволення| від зв'язків
Зв'язок можна відкинути замінивши дію зв'язку силою|силоміць| реакції зв'язку.
 .
.
У проекціях на осі декартової системи координат це виглядатиме так:
 ,
,  ,
,  .
.
Відносний рух матеріальної точки|точки|
У багатьох завданнях|задачах| динаміки рух матеріальної точки|точки| розглядається|розглядує| відносно|відносно| системи відліку, яка рухається відносно інерціальної| системи відліку.
 Отримаємо|одержуватимемо| диференціальні рівняння руху матеріальної точки|точки| відносно|відносно| рухомої|жвавої,рухливої| системи відліку.
Отримаємо|одержуватимемо| диференціальні рівняння руху матеріальної точки|точки| відносно|відносно| рухомої|жвавої,рухливої| системи відліку.
 - інерціальна| система відліку,
- інерціальна| система відліку,
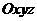 - рухома|жвава,рухлива| система відліку,
- рухома|жвава,рухлива| система відліку,
 ,
,
де  - сума активних сил,
- сума активних сил, 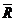 - сума сил реакції зв'язку.
- сума сил реакції зв'язку.
Згідно|згідно з| теоремі Коріоліса 
Перепишемо диференціальне рівняння таким чином:

Рисунок 4-3
Введемо|запроваджуватимемо| позначення:
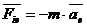 - переносна сила інерції,
- переносна сила інерції,
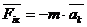 - коріолісова| сила інерції.
- коріолісова| сила інерції.
З урахуванням|з врахуванням| цих позначень ми отримуємо|одержуємо| динамічну теорему Коріоліса (рівняння відносного руху).
Матеріальна точка|точка| рухається|суне| відносно неінерціальної| системи відліку так само, як і відносно інерціальної|, тільки|лише| до прикладених активних сил і сил реакції зв'язків слід додати|добавляти| коріолісову| і переносну силу інерції.

Сили  і
і  є|з'являються,являються| поправками на неінерційність системи.
є|з'являються,являються| поправками на неінерційність системи.
У проекціях на рухомі|жваві,рухливі| осі
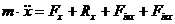


Дата добавления: 2018-05-12; просмотров: 885; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
