Объёмная плотность точечного заряда.




Рассмотрим систему из точеченого заряда 

Здесь возникает необходимость использовать 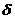 -функцию.
-функцию.

Тогда:



Это соответствует случаю, когда заряд помещён в начало координат, а плотность заряда ищется в точке, с радиус-вектором  .
. 
Если же заряд помещён не в начало отсчёта, то плотность заряда перепишется в следующем виде:

В случае системы точечных зарядов имеем:

Для изображения плотности точечного источника всегда используется 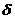 -функция.
-функция.
Закон сохранения заряда.
Запишем уравнение Максвелла:  . Подействуем на него оператором
. Подействуем на него оператором 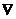 скалярно. Получаем:
скалярно. Получаем:

Но дивергенция всякого ротора равна нулю, поэтому в результате получаем:
 - уравнение непрерывности
- уравнение непрерывности
Проинтегрируем обе части этого уравнения по некоторому объёму:


 , где
, где 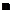 -единичный вектор нормали
-единичный вектор нормали
 определяет количество заряда выносимого через поверхность объёма. Если
определяет количество заряда выносимого через поверхность объёма. Если  - острый, то заряд выносится из объёма и
- острый, то заряд выносится из объёма и  -положителен. Если
-положителен. Если  тупой, то заряд приходит в объём и -
тупой, то заряд приходит в объём и -  имеет знак минус.
имеет знак минус.
Типы калибровок. Уравнения Даламбера для потенциалов

Перепишем уравнения Максвелла:


1.Калибровка Лоренца


Тогда уравнение первое уравнение Максвелла перепишется в следующем виде:

□  - оператор Даламбера
- оператор Даламбера
 □
□  - уравнение Даламбера
- уравнение Даламбера
Это уравнение есть – неоднородное дифференциальное уравнение в частных производных.
□- оператор гиперболического типа.
|
|
|
Для 4-го уравнения Максвелла имеем:


□ 
Все, имеющие физический смысл, результаты должны быть градиентно-инвариантыми:

В силу калибровки Лоренца получаем:
□ 
Т.е. функция 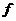 должна удовлетворять однородному уравнению Даламбера (его ещё называют волновым уравнением)
должна удовлетворять однородному уравнению Даламбера (его ещё называют волновым уравнением)
2.Калибровка Кулона
 - калибровка Кулона
- калибровка Кулона
Уравнение (А) перепишется в следующем виде:
 - уравнение Пуассона.
- уравнение Пуассона.
Если же  (в пустоте), то уравнение Пуассона принимает вид:
(в пустоте), то уравнение Пуассона принимает вид:
 -уравнение Лапласа.
-уравнение Лапласа.

получаем, что функция 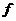 должна удовлетворять уравнению:
должна удовлетворять уравнению:

3.Калибровка поперечных волн

Полагаем 

 есть функция только координат.
есть функция только координат.

Значит функция 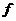 должна удовлетворять уравнению:
должна удовлетворять уравнению:



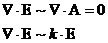 - здесь k – волновой вектор
- здесь k – волновой вектор
Уравнения Максвелла в среде без учёта пространственно-временной дисперсии. Переход от микро к макро




С помощью этих уравнений можно описывать электромагнитное поле в среде. В среде будем ставить индекс « 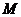 »=микро
»=микро
|
|
|

 включает в себя как связанные, так и свободные заряды в веществе. Каждой точке пространства ставится в соответствие функция
включает в себя как связанные, так и свободные заряды в веществе. Каждой точке пространства ставится в соответствие функция  . Это значит, что мы заменяем реальную среду моделью – сплошной средой, т.е. мы свойства разных точек «размазываем» по пространству. Существуют следующие способы описания сплошной среды на основе реальной среды:
. Это значит, что мы заменяем реальную среду моделью – сплошной средой, т.е. мы свойства разных точек «размазываем» по пространству. Существуют следующие способы описания сплошной среды на основе реальной среды:
1. Усреднение по некоторому физическому объёму  и времени
и времени  .
.
2. Статистическое усреднение. Считаем что у нас есть макроскопически-идентичный ансамбль систем(т.е. все внешние условия одинаковы). Здесь производятся измерения для отдельных ансамблей, а потом происходит усреднение. Этот способ более предпочтителен.
Усреднение будем обозначать символами «< >». Отметим, что усреднение коммутативно с дифференциальными операторами.
Итак, усредняем:
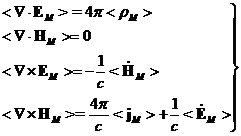


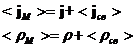
Среда под действием внешнего электромагнитного поля поляризуется, т.е. реагирует на внешнее воздействие. В случае, когда отсутствует пространственная дисперсия, поляризация характеризуется векторами электрической и магнитной поляризации  . Можно показать, что
. Можно показать, что  и
и 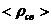 выражаются через
выражаются через  :
:
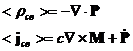

Введём обозначения: 

 ;
; 
|
|
|

Перенесём второе слагаемое из правой части в левую и объединим его с  :
:



Итак, уравнения Максвелла для среды имеют вид:

§30.* Теорема Стокса.
 - теорема Стокса
- теорема Стокса


 - Теорема Гаусса в операторной форме
- Теорема Гаусса в операторной форме
Например 



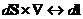 - теорема Стокса в операторной форме.
- теорема Стокса в операторной форме.
У. 7. Задача 14
14. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:
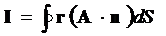 ,
, 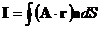
если объем, который охватывает замкнутая поверхность, равен V; A –постоянный вектор.
Решение. Умножим искомый интеграл на постоянный вектор р:


Так как вектор рпроизволен, то
 .
.
Аналогично показывается, что

§31*. Функциональные соотношения различных полей

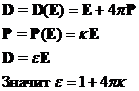

Здесь  - диэлектрическая проницаемость, а
- диэлектрическая проницаемость, а  - диэлектрическая восприимчивость.
- диэлектрическая восприимчивость.
 -разложение функции
-разложение функции 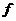 в ряд Маклорена.
в ряд Маклорена.
Если же  :
:

Возможно разложить  по векторам
по векторам  в ряд Маклорена:
в ряд Маклорена:

Первое слагаемое – это индукция, связанная с собственным дипольным моментом в отсутствие внешнего поля (собственная поляризация) – пироэлектрики.
|
|
|
Второе слагаемое – линейные среды.
Третье слагаемое – учёт нелинейности среды.
Среды, для которых нелинейные члены в разложении индукции по полю имеют вес, называются нелинейными.
Линейные среды
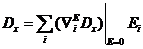
Введём обозначение:  , тогда
, тогда

Аналогично вводятся тензоры: 

Для ферромагнетиков  - учёт нелинейности.
- учёт нелинейности.
Неоднородные среды
Среды, для которых материальные характеристики (  ) являются функциями координат.
) являются функциями координат.

Т.е. характеристики трансляционно неинвариантны.
Введём понятие сплошной среды. Сплошная среда – это среда в каждой точке которой измерение материальных характеристик даёт не нулевой результат. Сплошная среда – это модель. В реальной среде имеются микро-пустоты, т.е. вещество локализовано в некоторых точках пространства. Чтобы перейти к сплошной среде, нужно усреднить микро-параметры по достаточно большому объёму.
Анизотропные среды

Анизотропные среды (свойства), это такие среды, свойства которых зависят от направления, в котором это свойство измеряется.
 Пусть в каком-то направлении исследуются оптические свойства среды. Затем мы повернули направление исследования, и оптические свойства изменились, т.е. оптические свойства зависят от угла поворота.
Пусть в каком-то направлении исследуются оптические свойства среды. Затем мы повернули направление исследования, и оптические свойства изменились, т.е. оптические свойства зависят от угла поворота.
Так как свойства меняются, то они неинвариантны относительно вращения. Этим свойством обладает всякая анизотропная среда.
Для тензоров 2-го ранга есть исключения:
Кубические системы описываются тензорами изотропного вида, т.е.

Монокристалл – есть однородная анизотропная среда.
§32*. Условия на границе раздела двух сред.
Рассмотрим поведение электромагнитного поля при переходе через границу раздела двух сред с различными материальными характеристиками. Используем теорему Остроградского-Гаусса и теорему Стокса:
Теорема Остроградского-Гаусса:

т.е. совершается следующий переход:

Теорема Стокса:


Запишем первое и четвёртое уравнения Максвелла в среде:

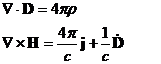
Имеется граница раздела – поверхность, отделяющая одну среду от другой.

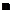 - нормаль к поверхности.
- нормаль к поверхности.


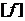 - скачок функции на границе раздела двух сред.
- скачок функции на границе раздела двух сред.
Рассмотрим цилиндр, образующие которого перпендикулярны поверхности  . По объёму
. По объёму  проинтегрируем первое и уравнение Максвелла:
проинтегрируем первое и уравнение Максвелла:

Воспользуемся теоремой Остроградского-Гаусса:


При  а следовательно и
а следовательно и 

В последнем равенстве мы воспользовались теоремой о среднем.
Аналогично:

Тогда:

Где ~h – боковая поверхность
В пределе, при 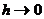 ,
, 

 - заряд на поверхности раздела двух сред
- заряд на поверхности раздела двух сред 


Пусть в пределе  , при этом
, при этом

Поверхностная плотность заряда: 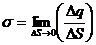
В результате получаем:

Если на поверхности нет свободных зарядов, то  и
и  , т.е.
, т.е. 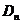 - непрерывна.
- непрерывна.
Аналогично рассмотрев второе уравнение Максвелла

Получим

Т.е. 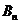 - всегда непрерывна, её скачок всегда равен нулю.
- всегда непрерывна, её скачок всегда равен нулю.
Теперь рассмотрим четвёртое уравнение Максвелла

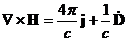

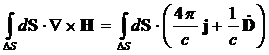 , причём
, причём 
Тогда по теореме Стокса:


Рассмотрим правую часть этого равенства:

Второе слагаемое, при 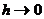 даёт 0.
даёт 0.
 - ток, протекающий через поверхность
- ток, протекающий через поверхность  , причём ток положителен в направлении нормали
, причём ток положителен в направлении нормали 
При  ,
, 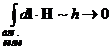
Воспользуемся теоремой о среднем:

Рассмотрим предельный переход при 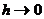 , тогда
, тогда 
 - поверхностный ток, текущий через
- поверхностный ток, текущий через 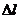 перпендикулярно чертежу.
перпендикулярно чертежу.

При  - ток, текущий по поверхности, в расчёте на длину.
- ток, текущий по поверхности, в расчёте на длину.

В результате получаем:

Если  , то
, то 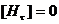 - непрерывна.
- непрерывна.
Аналогично для третьего уравнения Максвелла:

Имеем:

Т.е. тангенциальная составляющая электрического поля непрерывна.
Определим 
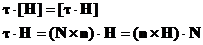
тогда 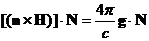
Ввиду произвольности  , это выражение эквивалентно выражению:
, это выражение эквивалентно выражению:


Дата добавления: 2018-05-12; просмотров: 881; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
