Малые колебания и свойства потенциальной энергии.
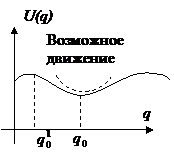
Рассмотрим систему с одной степенью свободы и исследуем функцию 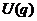 на экстремумы.
на экстремумы.
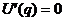 (отсюда получаем координаты точек равновесия для графика).
(отсюда получаем координаты точек равновесия для графика).
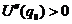
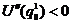
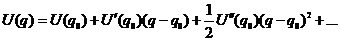 (21.1)
(21.1)
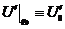 или
или 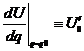 ;
; 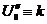 ;
; 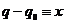
Итак: 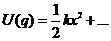 , т.к.
, т.к. 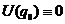 ,
, 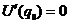 ,
, 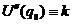 ,
, 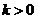 .
.
Отбросим в (21.1) слагаемые, начиная с третьего члена - получим параболический вид потенциальной энергии.
Если потенциальная энергия возрастает при удалении от положения равновесия, то в этом случае 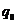 - точка устойчивого равновесия.
- точка устойчивого равновесия.
Рассмотрим точку 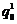
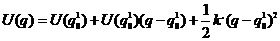
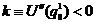 ,
, 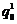 - точка неустойчивого равновесия.
- точка неустойчивого равновесия.
Колебания называются малыми, если в разложении последующие члены значительно меньше первых трёх:
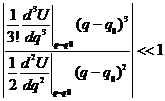
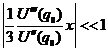
Колебания, удовлетворяющие этому условию, называются линейными (гармоническими). Учёт последующих членов приводит к нелинейности или ангармоничности колебаний.
[§19.] Колебания с одной степенью свободы. Характеристическое уравнение.
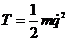 - кинетическая энергия.
- кинетическая энергия.
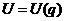 - потенциальная энергия.
- потенциальная энергия.
Введём 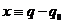 :
:
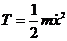 ,
, 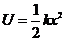
Функция Лагранжа: 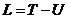
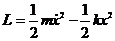
Уравнение движения : 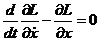
Получим: 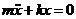 - простое линейное однородное дифференциальное уравнение второго порядка.
- простое линейное однородное дифференциальное уравнение второго порядка.
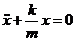
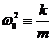
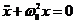 (22.1)
(22.1)
Для решения необходимы начальные условия:
1. 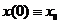
2. 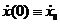
Пусть 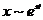 (временная зависимость через экспоненту).
(временная зависимость через экспоненту).
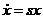
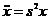
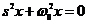
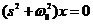
В общем случае 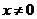 , тогда получим характеристическое уравнение:
, тогда получим характеристическое уравнение:
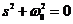
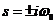
Имеем два корня, тогда общее решение можно записать в виде:
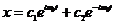
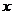 - должно быть вещественной величиной, следовательно
- должно быть вещественной величиной, следовательно 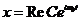 .
.
|
|
|
Вернемся к уравнению (22.1). Имеем решение 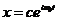
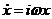 ,
,  .
.
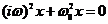
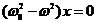
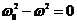 (22.2)
(22.2)
Уравнение (22.2) определяет частоты, возможные для данной системы - дисперсионное уравнение. Таким образом, получаем
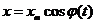
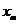 - амплитуда.
- амплитуда.
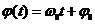 - фаза.
- фаза.
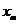 ,
,  - константы, определяемые из начальных условий.
- константы, определяемые из начальных условий.
Примеры колебаний:
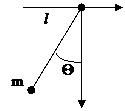
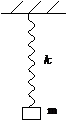
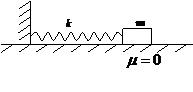
У. 4. Задачи 8-10
8. Выразить амплитуду 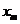 и начальную фазу
и начальную фазу 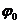 колебаний через
колебаний через 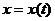 начальные значения x0, v0 координаты и скорости.
начальные значения x0, v0 координаты и скорости.
Ответ: 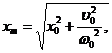
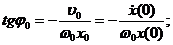
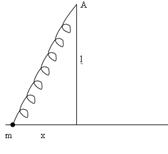 |
9.Найти частоту колебаний точки с массой m, способной двигаться по прямой и прикреплённой к пружине, другой конец которой закреплён в точке А на расстоянии l от прямой. Пружина, имея длину l, натянута с силой F.
Решение. Потенциальная энергия пружины (с точностью до малых величин высшего порядка) равна произведению силы F на удлинение δl пружины. при x<<l имеем:
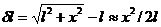 ,
,
так что U=Fx2/2l. Поскольку кинетическая энергия есть 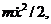 то
то
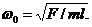
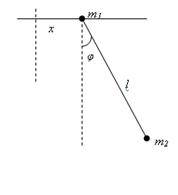
10. Найти частоту колебаний маятника, точка подвеса которого (с массой m1 в ней) способна совершать движение в горизонтальном направлении.
 |
|
|
|
Решение. При φ<<1 находим:
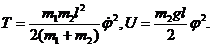
Отсюда
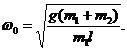
§20*. Колебания с n степенями свободы. Дисперсионное уравнение. Примеры 1-3.
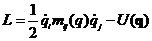 , где
, где 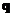 -
- 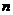 -мерный вектор.
-мерный вектор.
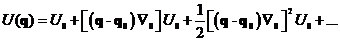
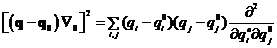
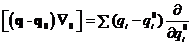
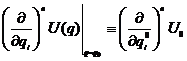
В точке 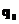 - экстремум(минимум):
- экстремум(минимум):
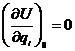
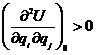 - условие минимума, оно понимается в смысле квадратичных форм, т.е. если умножить на вектор слева и на вектор справа, то образуется положительная скалярная величина:
- условие минимума, оно понимается в смысле квадратичных форм, т.е. если умножить на вектор слева и на вектор справа, то образуется положительная скалярная величина:
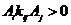 , для
, для 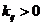
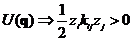 , где
, где 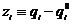

Тогда функция Лагранжа имеет вид:
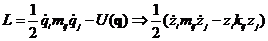
она описывает малые свободные гармонические колебания.
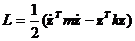
Уравнение движения для данной системы:
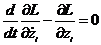
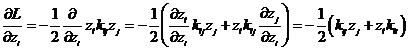
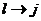
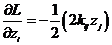
Аналогично можно получить:
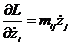
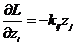
Подставим полученные формулы в уравнение движения, тогда получим:
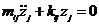
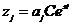
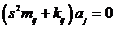 - система линейных однородных дифференциальных уравнений.
- система линейных однородных дифференциальных уравнений.
Эта система имеет нетривиальное решение, если:
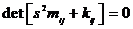 => характеристическое уравнение
=> характеристическое уравнение
Это матрицы 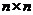 с действительными коэффициентами.
с действительными коэффициентами.
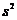 имеет
имеет 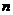 решений
решений 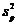 ,
, 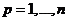
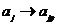 , где
, где 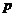 - номер корня.
- номер корня.
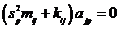
умножим это выражение на 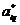 и просуммируем:
и просуммируем:
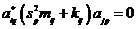 ,
, 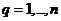
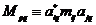
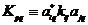
Получаем:
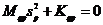 -матричное уравнение
-матричное уравнение
пусть 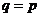 :
:
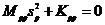 ,
, 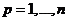
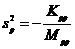
т.к. 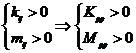 , тогда:
, тогда:
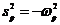
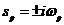
Из определения матриц 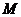 и
и 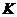 следует, что
следует, что
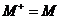
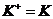
Можно показать, что 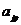 - вещественные числа, тогда
- вещественные числа, тогда 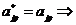
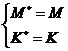
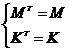 т.е. матрицы симметричные, значит:
т.е. матрицы симметричные, значит:
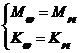 (23.1)
(23.1)
|
|
|
Запишем два матричных уравнения:
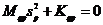
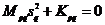
Вычтем из первого уравнения второе.
Воспользуемся свойством (23.1) и сложим два этих уравнения:
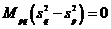
т.к. корни различны, то при 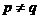 получаем
получаем 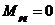 .
.
Если 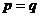 , то
, то 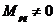 , но она неопределённая. Эта неопределённость исключается нормировкой:
, но она неопределённая. Эта неопределённость исключается нормировкой:
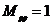
Эта нормировка позволяет найти неопределённый параметр 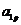 для всех корней.
для всех корней.
Таким образом:
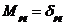
Рассмотрим матрицу 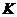 :
:
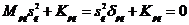
тогда:
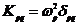 , где
, где 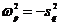
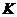 -диагональная матрица.
-диагональная матрица.
Тогда 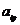 - преобразование с помощью которого
- преобразование с помощью которого 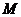 переводится в единичную, а
переводится в единичную, а 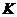 диагонализируется.
диагонализируется.
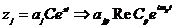
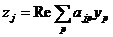 , где
, где 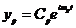
Тогда:
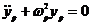
Переменные 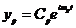 - нормальные координаты, или главные колебания. Это простейшая форма колебаний.
- нормальные координаты, или главные колебания. Это простейшая форма колебаний.
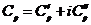 - комплексная константа.
- комплексная константа.
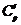 и
и 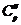 находятся из начальных условий:
находятся из начальных условий:
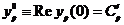
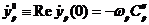
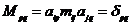 , и
, и 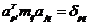 , т.е.
, т.е. 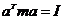 - единичная матрица.
- единичная матрица.
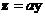
для того чтобы получить единицу перед 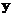 надо левую и правую часть умножить на
надо левую и правую часть умножить на 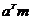 :
:
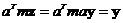
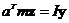
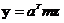
Для компоненты 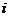 :
:
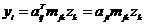
Начальные условия:
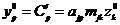
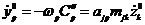
Схема решения задач:
1. Составить дисперсионное уравнение.
2. решаем, находим корни(собственные частоты)
3. находим решения для нормальных координат
4. из решения уравнений находим коэффициент 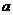 :
:
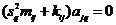 характеристическое уравнение
характеристическое уравнение
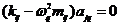 дисперсионное уравнение
дисперсионное уравнение
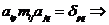 находим матрицу,
находим матрицу, 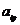 искомый коэффициент.
искомый коэффициент.
|
|
|
5. зная 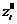 и
и 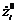 находим
находим 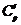 и
и 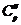
6. через 3. находим 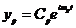
7. находим 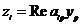
Примеры:





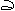

 1. Рассмотрим колебательный LC-контур
1. Рассмотрим колебательный LC-контур
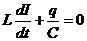 ,
, 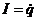
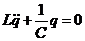
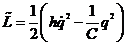 - функция Лагранжа для данной системы.
- функция Лагранжа для данной системы.
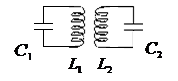 |
2. Рассмотрим контур
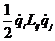 - энергия, связанная с наличием индуктивности в системе,
- энергия, связанная с наличием индуктивности в системе,
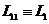
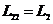
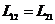
Энергия, связанная с конденсатором 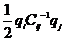 ,
,
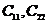 - емкости
- емкости
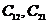 - электростатическая индукция
- электростатическая индукция
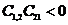
Задачу эту необходимо упрощать.
3. Рассмотрим задачу:
Свободные колебания двухатомной молекулы.
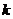
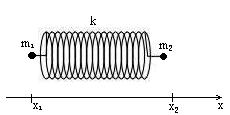 - коэффициент взаимодействия.
- коэффициент взаимодействия.
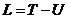
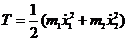
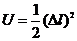
здесь 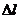 - удлинение по сравнению с равновесным состоянием пружины.
- удлинение по сравнению с равновесным состоянием пружины.
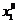 ,
, 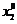 - координаты точек в отсутствии деформации пружины.
- координаты точек в отсутствии деформации пружины.
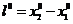
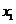 ,
, 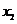 - координаты точек в деформированном состоянии
- координаты точек в деформированном состоянии
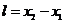
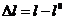
Можем найти потенциальную энергию.
Вводим переменные 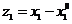 и
и 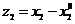
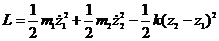
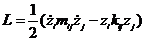
Найдём 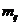 и
и 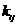 :
:
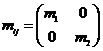 и
и 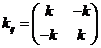
1. Составим дисперсионное уравнение:
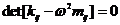
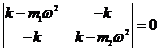
Решая его получим два корня:
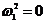 и
и 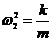
2. Напишем дифференциальные уравнения для нормальных колебаний:
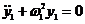 - здесь колебаний нет, т.к.
- здесь колебаний нет, т.к. 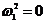
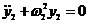
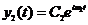 , где
, где 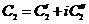
3. Найдём матрицу 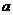 .
.
Используем уравнения: 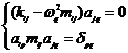
Пусть 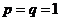 , тогда:
, тогда:
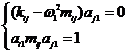
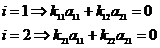
значит 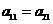 .
.
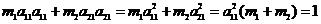
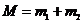
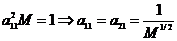
Аналогично рассуждая для 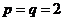 получим:
получим:
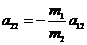
и из условия нормировки:
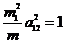 , где
, где 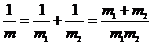
тогда:
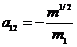 ,
, 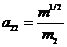
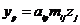 ,
, 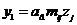 , но
, но 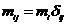 - диагональная, тогда:
- диагональная, тогда:
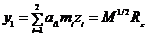
Здесь 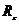 - координата центра масс
- координата центра масс
Рассуждая аналогично для 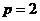 , получим:
, получим:
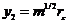 , где
, где 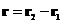
Пусть 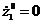 ,
, 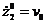 ,
, 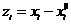 , тогда:
, тогда:
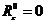 и
и 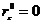
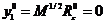
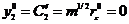
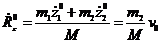
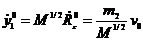
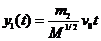
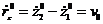 , тогда
, тогда 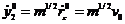
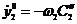
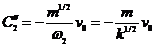
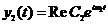
Подставляя сюда выражения для 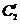 и
и 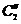 получим:
получим:
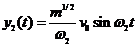
Итак, решение задачи:
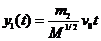
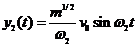
У. 5. Задача 11
1. Определить малые колебания двойного плоского маятника.
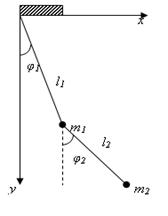 |
Решение. Для малых колебаний
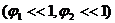 найденная в задаче 1 параграфа 6 функция Лагранжа принимает вид :
найденная в задаче 1 параграфа 6 функция Лагранжа принимает вид :
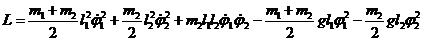 .
.
Уравнения движения:
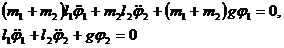
После подстановки (23,6) :

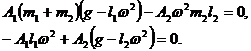
Корни характеристического уравнения:
Ответ: 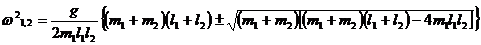 .
.
При 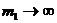 частоты стремятся к пределам
частоты стремятся к пределам 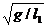 и
и 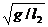 , соответствуют независимым колебаниям двух маятников.
, соответствуют независимым колебаниям двух маятников.
§21. Оператор 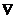 .
.
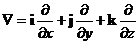
Оператор набла – векторный дифференциальный оператор. Оператор набла можно ввести по-другому:
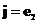
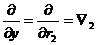
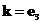
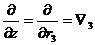
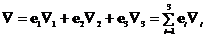
Часто знак суммы опускают (правило суммирования Эйнштейна).
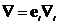
Запишем условие ортонормированности рассматриваемого базиса:
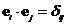
Действия оператора набла:
1. Оператор набла действует на скалярную функцию F:
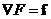 или
или 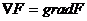
2. Оператор набла скалярно действует на векторную функцию 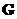 :
:
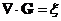
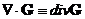
3. Оператор набла векторно умножается на векторную функцию 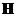 :
:
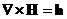
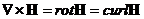
Кроме векторного и скалярного, есть ещё смешенное произведение векторов:
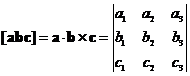 - объем параллелепипеда.
- объем параллелепипеда.
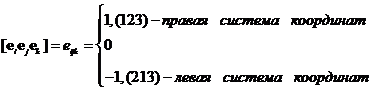
 - единичный антисимметричный тензор третьего ранга.
- единичный антисимметричный тензор третьего ранга.
У. 6. Задачи 12, 13
12. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.
Решение. 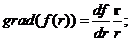
13. Вычислить 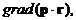
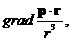
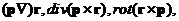 где p – постоянный вектор.
где p – постоянный вектор.
Решение. 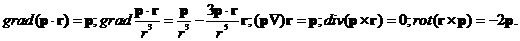
[§22.] Уравнения Максвелла для электромагнитного поля в вакууме.
Будем использовать гауссову систему единиц.
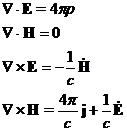


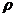 и
и 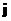 являются источниками поля. Уравнения Максвелла позволяют по заданным источникам рассчитать электромагнитное поле. Уравнениям Максвелла в дифференциальной форме ставятся в соответствие уравнения в интегральной форме.
являются источниками поля. Уравнения Максвелла позволяют по заданным источникам рассчитать электромагнитное поле. Уравнениям Максвелла в дифференциальной форме ставятся в соответствие уравнения в интегральной форме.
[§23.] Потенциалы электромагнитного поля в вакууме.
Удобно ввести:
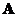 -векторный потенциал
-векторный потенциал
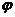 -скалярный потенциал
-скалярный потенциал
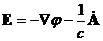
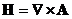
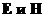 однозначно определяют электромагнитное поле
однозначно определяют электромагнитное поле
[§24.] Градиентная инвариантность.
Существует преобразование, которое не меняет полевых характеристик 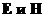 . Таким преобразованием является градиентное:
. Таким преобразованием является градиентное:
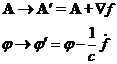
Здесь 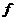 – произвольная функция координат и времени
– произвольная функция координат и времени 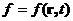
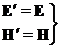 -инвариантность полевых характеристик
-инвариантность полевых характеристик
относительно градиентных преобразований.
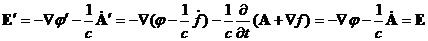
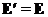
Аналогично для 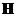 :
:
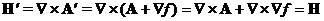
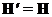
На потенциалы 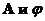 могут быть наложены произвольные, удобные для исследования ограничения – калибровки потенциалов, т.к.
могут быть наложены произвольные, удобные для исследования ограничения – калибровки потенциалов, т.к. 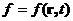 - произвольная.
- произвольная.
§25*. 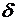 -функция.
-функция.
Пусть имеется функция Хевисайда:
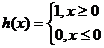

Ясно, что кроме 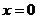 , производная везде равна нулю. Рассчитаем интеграл:
, производная везде равна нулю. Рассчитаем интеграл:
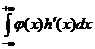 ,
, 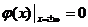 ,
, 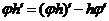
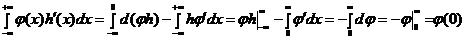
Рассмотрим этот же случай, но картинка смещена на  :
:
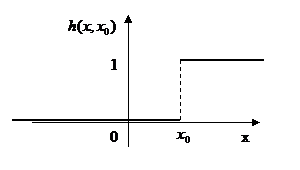
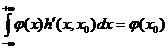
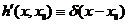
Интегральное одномерное соотношение:
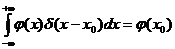
Существует множество способов моделирования подобных функций.
Если 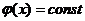 , то (3) это :
, то (3) это : 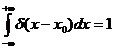
Рассмотрим простейший случай.
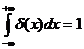 - площадь под графиком функции:
- площадь под графиком функции:
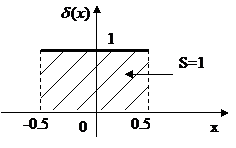
Делим  пополам.
пополам.
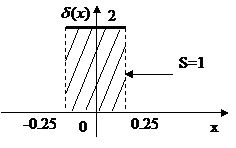

И так далее до бесконечности. Это одна из простейших моделей 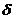 -функции.
-функции.
Дата добавления: 2018-05-12; просмотров: 544; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
